
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Все КЕ для двух высказываний
Таблица 8 Все КН для двух высказываний
Развёртывание элементарных конъюнкций 1. В развертываемую элементарную конъюнкцию ранга 2. Каждая единица представляется в виде 3. Производится раскрытие всех скобок на основе распределительного закона 1-го рода, что приводит к развертыванию исходной конъюнкции ранга Пример. Развернуть конъюнкцию 1. 2. 3. =
Развёртывание элементарной дизъюнкции 1. В развертываемую дизъюнкцию ранга 2. Каждый нуль представляется произведением 3. Полученная сумма преобразуется с помощью распределительного закона 2-го рода в логическое произведение Пример. Развернуть дизъюнкцию
Упражнения 1. Используя алгебраические преобразования, доказать тождественную истинность или тождественную ложность формул: 1) 4) 6) 9)
2. Доказать равносильности формул, не используя таблицы истинности: 1) 5) 8) 11) 3. Упростить формулы: 1) 5) 4.Привести следующие ниже формулы к базиса 1) 5. Развернуть конъюнкцию: 1) Развернуть дизъюнкцию: 3) 1. 5. Функции алгебры логики. Нормальные формы логических Функций Логическая функция [функция алгебры логики (ФАЛ)] Как нетрудно заметить, приведенное определение ФАЛ полностью совпадает с определением формулы, данным в подразделе 1.3. Таким образом, всякая формула алгебры логики есть функция алгебры логики, в которой простые высказывания воспринимаются уже как переменные
Набор логических переменных, или, иначе входной набор, – это определенная комбинация значений переменных в логической функции. Максимальное число различных входных наборов есть величина Полностью определенная функция – это логическая функция, принимающая значение 0 или 1 на всех входных наборах. Частично определенная функция – это логическая функция, значения которой определены не на всех входных наборах. Такие наборы называют безразличными. Частично определенную логическую функцию можно сделать полностью определенной, приписав безразличным наборам произвольные значения: 0 или 1. Используя законы и аксиомы алгебры логики и их следствия, можно получать логические выражения в различных формах. Среди них имеются такие формы, к которым можно свести любую логическую функцию. Такие формы определяют канонический вид логической функции. В алгебре логики каноническими принято считать нормальную дизъюнктивную форму (НДФ) и нормальную конъюнктивную форму (НК Ф) и соответственно совершенную НДФ (СНДФ) и совершенную НКФ (СНКФ). НДФ – это дизъюнкция нескольких элементарных конъюнкций. Эта форма называется нормальной, так как все ее члены имеет вид элементарных конъюнкций. Вследствие того, что все члены соединены в одну функцию знаком дизъюнкции, форма носит название дизъюнктивной. И, наконец, форма называется совершенной, если её члены имеют высший ранг, являясь конституентами единицы или нуля.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.151.141 (0.006 с.) |










 вводятся в качестве дополнительных сомножителей
вводятся в качестве дополнительных сомножителей  единиц, где
единиц, где  – число высказываний и
– число высказываний и  .
. , где
, где  – высказывание, отсутствующее в исходной конъюнкции.
– высказывание, отсутствующее в исходной конъюнкции.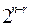 КЕ.
КЕ. . Здесь предполагается, что число высказываний
. Здесь предполагается, что число высказываний  , но два из них отсутствуют, тогда:
, но два из них отсутствуют, тогда:
 .
.
 .
. , где
, где  . Здесь число высказываний
. Здесь число высказываний  , отсутствует высказывание
, отсутствует высказывание  :
: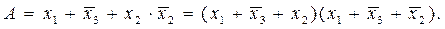
 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5) 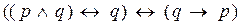 ;
; ; 7)
; 7)  ; 8)
; 8)  ;
; .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
; ; 6)
; 6)  ; 7)
; 7)  ;
; ; 9)
; 9)  ; 10)
; 10)  ;
;
 .
. 2)
2) 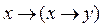 ; 3)
; 3) 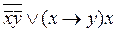 ; 4)
; 4)  ;
; ;
;
 ; 2)
; 2)  ; 3)
; 3)  .
.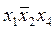 ; 2)
; 2) 
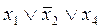 ; 4)
; 4) 
 – это выражение, представляющее собой сложное высказывание, состоящее из нескольких простых высказываний
– это выражение, представляющее собой сложное высказывание, состоящее из нескольких простых высказываний  , связанных соединительными словами. Это сложное высказывание принимает значения 0 или 1 на всех наборах логических значений всех простых высказываний.
, связанных соединительными словами. Это сложное высказывание принимает значения 0 или 1 на всех наборах логических значений всех простых высказываний.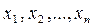 . Это правомочно, так как каждое из них принимает два значения: 0 или 1. А в зависимости от этого логические значения выражения тоже будут принимать значения 0 или 1, т.е. выражение является функцией в общепринятом смысле.
. Это правомочно, так как каждое из них принимает два значения: 0 или 1. А в зависимости от этого логические значения выражения тоже будут принимать значения 0 или 1, т.е. выражение является функцией в общепринятом смысле. , где
, где 


