
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выполнимость и общезначимость формул
Определение 1. Формула Bлогики предикатов называется выполнимой в области M, если существуют значения переменных, входящих в эту формулу и принадлежащих множеству M, при которых формула Bпринимает истинные значения. Это определение очень похоже на то определение, которое мы дали для квантора существования в подразд. 3.1 относительно одного предиката. Данное определение отличается тем, что оно применяется не к отдельному предикату, а к формуле, состоящей из нескольких предикатов. Определение 2. Формула Bназывается выполнимой, если существует область, на которой эта формула выполнима. Это определение не следует понимать так, что если формула выполнима, то она выполнима в любой области. Для выполнимости формулы достаточно существования любой области, на которой она выполнима. Определение 3. Формула Bназывается тождественно истинной в области M, если она принимает истинные значениядля всех значений переменных, входящих в эту формулу и принадлежащих множеству M. Это определение по форме похоже на определение 2 подразд. 3.1., но отличается от него тем, что то определение давалось для предиката, а данное – для формулы, т.е. для предложения, состоящего из нескольких предикатов. Определение 4. Формула Bназывается общезначимой, если она тождественно истинная на всякой области. Ранее в подразд. 2.9., мы вскользь упомянули о понятии общезначимость и отметили, что его используют иногда для обозначения тождественно истинных формул алгебры логики и обозначают символом ╞. Таким образом, мы видим, что преемственность и аналогия полностью сохраняются. И в алгебре логики, и в логике предикатов термин общезначимость употребляется для обозначения одинаковых по смыслу понятий – тождественно истинных формул. Только в логике предикатов понятие тождественно истинной формулы более широкое, чем в алгебре логики. Определение 5. Формула Как нетрудно видеть, это определение с точностью до обозначений совпадает с определением тождественно ложного предиката (определение 2, подразд. 3.1) и тождественно ложной формулы алгебры логики (определение 2, подразд. 1.3).
Из приведенных определений вытекают следующие свойства формул логики предикатов. 1. Если формула Bобщезначимая, то она и выполнима на всякой области. 2. Если формула B тождественно истинная в области M, то она и выполнима в этой области. 3. Если формула B тождественно ложная в области M, то она и не выполнима в этой области. 4. Если формула B не выполнима, то она тождественно ложна на всякой области. На основании приведенных определений выделяют два класса формул логики предикатов: выполнимых и не выполнимых формул. Рассмотрим примеры выполнимых, невыполнимых и общезначимых формул. Пусть формула задана в виде: Если же предикат Рассмотрим другой пример. Пусть заданы предикаты: P(x)– “число Так как для предиката P(x) Кроме того, какие бы числа y и y мы ни взяли соответственно из Если же предикат
Интерес представляют общезначимые формулы, так как они являются логическими законами. Такой простейшей формулой является формула Если квантор всеобщности применить к конъюнкции любого предиката В то же время Рассмотрим еще один пример, показывающий, как с помощью равносильных преобразований устанавливается общезначимость формул логики предикатов:
Таким образом, мы получили заданную формулу, которая является тождественно истинной для любых двух одноместных предикатов и в любой области (поскольку область заранее не оговаривалась). Значит, формула общезначима. Упражнения 1. Являются ли тождественно истинными следующие формулы: 1) 3) 2. Привести к предваренной нормальной форме следующие формулы логики предикатов: 1) 3) 5) 3. Какие из приведенных ниже формул являются общезначимыми: 1) 3) 4) 5)
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.208 (0.014 с.) |
 называется тождественно ложной в области M, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и принадлежащих множеству M.
называется тождественно ложной в области M, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и принадлежащих множеству M. , где предикат
, где предикат  означает
означает  и определен на области
и определен на области  , где
, где  (символ
(символ  означает, что рассматриваемая переменная x принимает значения от a до b, то же самое и для
означает, что рассматриваемая переменная x принимает значения от a до b, то же самое и для  ). Ясно, что в этом случае формула
). Ясно, что в этом случае формула  рассматривать в другой области, например
рассматривать в другой области, например  , где
, где  , то формула
, то формула  кратно 7”, Q (у) – “число
кратно 7”, Q (у) – “число  , определенные в области
, определенные в области  . На какой области формула
. На какой области формула  выполнима, невыполнима и является ли она общезначимой? Дадим ответы на эти вопросы.
выполнима, невыполнима и является ли она общезначимой? Дадим ответы на эти вопросы. , а для предиката Q(x)
, а для предиката Q(x) 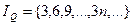
 , то для предиката
, то для предиката 
 . А это означает, что существуют такие
. А это означает, что существуют такие  и
и 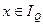 , что среди натуральных чисел N всегда найдется такое число, при котором будет истинна формула
, что среди натуральных чисел N всегда найдется такое число, при котором будет истинна формула  . Например, для чисел
. Например, для чисел  и
и  существует число
существует число  (это же число принадлежит и каждому в отдельности множеству
(это же число принадлежит и каждому в отдельности множеству  и
и  ). Следовательно, рассматриваемая формула является истинной на множестве
). Следовательно, рассматриваемая формула является истинной на множестве  , т.е. она выполнима в этой области (на этом множестве), а следовательно, и в области M.
, т.е. она выполнима в этой области (на этом множестве), а следовательно, и в области M. , где
, где  , то формула
, то формула  не найдется ни одной такой пары чисел, для которой были бы истинны предикаты
не найдется ни одной такой пары чисел, для которой были бы истинны предикаты  . Причем, независимо от конкретного смыслового содержания предиката
. Причем, независимо от конкретного смыслового содержания предиката  , эта формула является тождественно истинной в любой области M. Действительно,
, эта формула является тождественно истинной в любой области M. Действительно,  .
. , т.е.
, т.е.  . Действительно,
. Действительно, 
 значит, формула
значит, формула  является логическим законом.
является логическим законом.



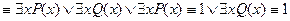 .
. ; 2)
; 2) 
 ;
; ; 4)
; 4)  ?
? ; 2)
; 2)  ;
; ; 4)
; 4)  ;
;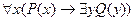 .
. ; 2)
; 2)  ;
; ;
; ;
; .
.


