
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тогда правило подстановка схематически запишется так
Читается эта запись следующим образом: “Если формула 2. Правило заключения (ПЗ – modus ponens) Если формулы
Определение доказуемой формулы Исходя из приведенных в предыдущем подразделе 11 аксиом и 2 простейших правил вывода, уточним понятие доказуемой формулы. а) всякая аксиома является доказуемой формулой; б) формула, полученная из доказуемой формулы путем применения правила подстановки, есть доказуемая формула; в) формула г) никакая другая формула исчисления высказываний не считается доказуемой. Процесс получения доказуемых формул называют доказательством. Рассмотрим примеры получения доказуемых формул. 1. Доказать, что Воспользуемся аксиомой
и выполним подстановку
Применяя правило заключения к аксиоме
В формуле (2) осуществим подстановку В результате получим доказуемую формулу
Применяя правило заключения к аксиоме IV2и формуле (3), получим
Наконец, осуществив подстановку в формуле (4) вместо 2. Доказать, что
Выполнив подстановку
Покажем, что формулы
доказуемы. Возьмем аксиому
Применяя к аксиоме Возьмем аксиому
и получим
Применяя к аксиоме III2 и формуле (6) правило заключения, устанавливаем доказуемость формулы (4). Применяя правило заключения к формулам (3) и (2), получим доказуемую формулу
Применяя правило заключения к формулам (4) и (7), получим доказуемость исходной формулы.
Производные правила вывода Кроме двух простейших правил вывода, рассмотренных выше, используются и производные правила вывода (более сложные). Они получаются путем использования простейших правил вывода и понятия доказуемой формулы. Рассмотрим эти правила.
1. Правило одновременной подстановки (ПОП). Пусть
Справедливость этой операции очевидна, поэтому доказывать ее не будем. 2. Правило сложного заключения (ПСЗ). Это правило применяется к формулам вида Схематически это правило записывается так:
ПСЗ легко доказывается последовательным применением ПЗ. Действительно, если формулы Продолжая эти рассуждения, мы докажем, наконец, что формула L доказуема. 3. Правило силлогизма (слово силлогизм греческое и означает дедуктивное логическое умозаключение). Если доказуемы формулы
Это правило аналогично свойству транзитивности в обычной алгебре: если Докажем справедливость правила силлогизма. Для этого сделаем следующие одновременные подстановки:
Получим доказуемые формулы
Кроме того, по условию
Из формул (4) и (2) согласно ПЗ получаем
Но тогда из формул (5), (3) и (1) согласно ПСЗ получаем
что и требовалось доказать. 4. Правило контрпозиции. Если доказуема формула
Доказательство. Сделаем одновременную подстановку
Но по условию доказуема формула
Из формул (2) и (1) согласно ПЗ имеем 5. Правило снятия двойного отрицания (ПСДО). Если доказуема формула
Если доказуема формула
Доказательство. Выполним подстановки
получим
Но по условию
Таким образом, из формул (3) и (2) по правилу силлогизма получаем
Упражнения 1. Применяя правило подстановки, показать, что доказуемы формулы:
2. Применяя правило подстановки и правило заключения, установить доказуемость формул: 1) 4) 3. Применяя производные правила вывода, показать, что доказуема формула 4. Доказать производные правила вывода: 1) Примечание. Отметим некоторые общие соображения для получения доказуемых формул. Если задана “короткая” формула, для которой надо установить её доказуемость, то нужно мысленно представить, на какую из аксиом она похожа по форме. Затем надо представить, какие переменные и на какие формулы надо в ней заменить, чтобы получить заданную доказуемую формулу. Если задана “длинная” формула, то нужно мысленно “охватить” одну, а лучше две её последние скобки, и представить, на какую из аксиом эти скобки “похожи” по форме. Затем надо представить, какие переменные в этой части формулы и на какие другие формулы надо заменить, чтобы получить заданную часть формулы. Замена в оставшейся начальной части заданной формулы уже будет практически очевидна. Примерно по такому же сценарию устанавливается доказуемость формулы путем применения правил подстановки и замены. Сначала надо представить, на последнюю часть какой из “длинных” аксиом “похожа” по форме заданная формула, и подобрать соответствующую замену переменным. Далее смотрят, нельзя ли к полученной промежуточной доказуемой формуле применить ПЗ или ПСЗ, чтобы получить заданную формулу. Если этого сделать нельзя, то смотрят на оставшиеся части промежуточной доказуемой формулы и определяют, на какие из “коротких” аксиом они “похожи”, и устанавливают тем самым их доказуемость. Затем, применяя ПСЗ, устанавливают доказуемость исходной формулы. Иногда после первого и даже второго применения правила подстановки бывает необходимо применить правило контрпозиции или снятия двойного отрицания, а уж затем применять ПЗ или ПСЗ. 2. 5. Определение формулы, выводимой из совокупности формул Н В исчислении высказываний некоторые формулы могут быть получены не только из совокупности аксиом, но и из совокупности формул Н, не являющихся аксиомами. Такие формулы называют выводимыми из совокупности формул Н. Дадим определение таким формулам. Пусть у нас имеется некоторая совокупность формул Тогда: 1) всякая формула 2) всякая доказуемая формула выводима из Н; 3) если формулы С и То, что некоторая формула В выводима из совокупности Н, записывают так: Число формул совокупности Н может быть самым различным. Если Н= 0, то предполагается, что совокупность (множество) Н не содержит никаких других формул, кроме аксиом исчисления высказываний. Если указано, что совокупность Н состоит из некоторых формул, например A,B,C, то предполагается (по умолчанию), что в эту совокупность входят и аксиомы. Причем формулы A, B и C не обязательно должны быть доказуемыми. Исходя из этого, можно отметить, что класс формул, выводимых из совокупности Н, совпадает с классом доказуемых формул в случае, когда совокупность Н содержит только доказуемые формулы, и в случае, когда совокупность Н пуста.
Если же совокупность формул Н содержит хотя бы одну недоказуемую формулу, то класс формул, выводимых из совокупности Н, шире класса доказуемых формул. Рассмотрим пример. Доказать, что из совокупности формул Доказательство. Так как
Возьмем аксиомы и выполним подстановки
Так как формула
Из формул (5) и (3) согласно ПЗ получаем
Из формул (2) и (4) согласно ПЗ получаем
Из формул (7) и (6) согласно ПЗ получаем
И, наконец, из формул (1) и (8) по тому же ПЗ получаем
Если мы запишем последовательность всех выводимых формул с номерами (1)…(9), то получим
Такая последовательность называется выводом формулы из совокупности формул Н. Теперь распространим понятие вывода на общий случай.
Понятие вывода Выводом из конечной совокупности формул Н называется всякая конечная последовательность формул 1) он является одной из формул совокупности Н; 2) он является доказуемой формулой; 3) он получается по ПЗ (для доказуемых и выводимых формул) из двух любых предшествующих членов последовательности Из определения выводимой формулы и вывода из совокупности формул Н следуют свойства вывода: 1) всякий начальный отрезок вывода из совокупности Н есть вывод из Н; 2) если между двумя соседними членами вывода из Н (в начале или в конце) вставить некоторый вывод из Н, то полученная новая последовательность формул будет выводом из Н. Например, если совокупности формул 3) всякий член вывода из совокупности Н является формулой, выводимой из Н; 4) если 5) для того чтобы формула В была выводима из совокупности формул Н, необходимо и достаточно, чтобы существовал вывод этой формулы из Н. При установлении доказуемости формул мы использовали аксиомы и вполне определенные правила вывода. Аналогично этому при получении формул, выводимых из совокупности Н, кроме определения выводимой формулы нужно использовать какие-то правила, пользуясь которыми можно было бы получать эти формулы. В отличие от правил вывода, используемых при установлении доказуемости формул, здесь также используются определенные правила, которые мы будем называть правилами выводимости.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.141.202 (0.069 с.) |
 .
. доказуема, то доказуема и формула
доказуема, то доказуема и формула  ”.
”.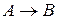 доказуемы в исчислении высказываний, то формула
доказуемы в исчислении высказываний, то формула  также доказуема. Схематическая запись этого правила имеет вид
также доказуема. Схематическая запись этого правила имеет вид
 путем применения правила заключения, есть доказуемая формула;
путем применения правила заключения, есть доказуемая формула; (эту формулу называют рефлексивностью импликации).
(эту формулу называют рефлексивностью импликации).

 . Тогда получим
. Тогда получим (1)
(1) и формуле (1), получим
и формуле (1), получим (2)
(2)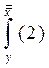
 (3)
(3) (4)
(4) формулы
формулы 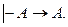

 . Возьмем аксиому
. Возьмем аксиому  и выполним в ней последовательно две подстановки, заменяя сначала
и выполним в ней последовательно две подстановки, заменяя сначала  , а затем
, а затем 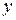 на
на  . В результате получим доказуемую формулу
. В результате получим доказуемую формулу (1)
(1) , получим
, получим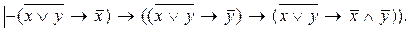 (2)
(2) ; (3)
; (3) (4)
(4) и выполним подстановку
и выполним подстановку  в результате получим
в результате получим (5)
(5) и формуле (5) правило заключения, получаем, что формула (3) доказуема.
и формуле (5) правило заключения, получаем, что формула (3) доказуема. и в ней переобозначим
и в ней переобозначим  Для нее выполним подстановку
Для нее выполним подстановку
 (6)
(6) (7)
(7)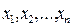 − переменные,
− переменные,  − любые формулы исчисления высказываний. Тогда результат одновременной подстановки в
− любые формулы исчисления высказываний. Тогда результат одновременной подстановки в  соответственно формул
соответственно формул  является доказуемой формулой. Схематично операция одновременной подстановки записывается так:
является доказуемой формулой. Схематично операция одновременной подстановки записывается так: .
. и формулируется так: если формулы
и формулируется так: если формулы  и
и  доказуемы, то доказуема и формула
доказуемы, то доказуема и формула  .
.
 и
и  . Но так как формулы
. Но так как формулы  и
и 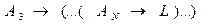
 , то доказуема формула
, то доказуема формула  т.е.
т.е.
 то
то 
 и
и 
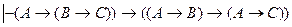 (1)
(1) (2)
(2) (3)
(3)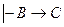 (4)
(4) (5)
(5) ,
, , т.е.
, т.е.
 в результате получаем
в результате получаем (1)
(1) , что и требовалось доказать.
, что и требовалось доказать. , то доказуема и формула
, то доказуема и формула 
 , то доказуема формула
, то доказуема формула 
 и
и  ,
, (1)
(1)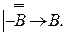
 (2)
(2) (3)
(3)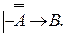 (4)
(4)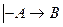 , а из формул (1) и (4) по тому же правилу получаем
, а из формул (1) и (4) по тому же правилу получаем 




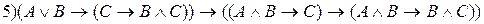
 ; 2)
; 2)  ; 3)
; 3) 
 5)
5) 

 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 

 является формулой, выводимой из Н;
является формулой, выводимой из Н; выводимы из совокупности Н, то формула В также выводима из Н (правило заключения для выводимых формул).
выводимы из совокупности Н, то формула В также выводима из Н (правило заключения для выводимых формул). .
. выводима формула
выводима формула  .
. и
и 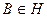 , то по определению выводимой формулы
, то по определению выводимой формулы (1)
(1) (2)
(2)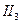
 и I
и I 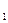

 и
и  В результате получим доказуемые формулы, которые выводимы из Н по определению, т.е.
В результате получим доказуемые формулы, которые выводимы из Н по определению, т.е. (3)
(3) (4)
(4) доказуема (см. подразд. 2.3), то она выводима из Н:
доказуема (см. подразд. 2.3), то она выводима из Н: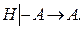 (5)
(5) (6)
(6) (7)
(7) (8)
(8) (9)
(9)
 , всякий член которой удовлетворяет одному из следующих трех условий:
, всякий член которой удовлетворяет одному из следующих трех условий: .
.
 и
и  являются выводами из Н, то совокупность
являются выводами из Н, то совокупность 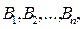
 ,
,  является тоже выводом из Н.
является тоже выводом из Н.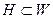 (
( − знак включения, читается: “множество Н включено в множество W “ или “ Н содержится в W “), то всякий вывод из совокупности Н является и выводом из совокупности W.
− знак включения, читается: “множество Н включено в множество W “ или “ Н содержится в W “), то всякий вывод из совокупности Н является и выводом из совокупности W.


