
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые применения алгебры логики
Еще в 1910 году физик Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-коммутационных схем (РКС). Однако его идеи стали использовать гораздо позже, когда создание общей теории РКС стало остро необходимым. Это было связано с появлением ЭВМ. Кстати, первая релейная ЭВМ Марк-1 была создана в США в 1944 году Г.Айткеном и установлена в Гарвардском университете. А уже в 1945 году в Пенсильванском университете был осуществлен проект первой электронной ЭВМ, получившей название ЭНИАК, которая была публично продемонстрирована в 1946 году. Использование алгебры логики при создании РКС основано на том, что в них основным техническим элементом является электромагнитное реле, имеющее два устойчивых состояния (включено/выключено). При включенном состоянии ток в цепи, в которой стоит реле, протекает через его контакты и не протекает при выключенном состоянии. Включенному состоянию сопоставляют цифру 1, а выключенному – цифру 0. Как мы уже видели ранее, в алгебре логики тоже используются два логических значения, которые мы обозначали теми же цифрами 0 и 1. Исходя из этого, оказалось возможным каждой РКС поставить в соответствие некоторую формулу (логическую функцию), а каждой формуле – некоторую РКС. Тогда изучение свойств РКС и ее упрощение можно заменить изучением и упрощением соответствующей формулы. Затем от упрощенной формулы можно перейти к схеме. Простейшая РКС содержит один переключатель P,имеет один вход А и один выход В. Переключателю Р можно поставить в соответствие высказывание “переключатель Р замкнут”. Если высказывание Р истинно, то сигнал, поступающий на вход А появится на выходе В. В этом случае схема проводит ток. Если высказывание Р ложно, то схема ток не проводит и на выход В сигнал не пройдет.

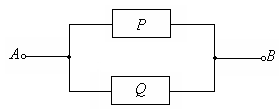
Если два переключателя соединить последовательно, как показано на рис.13, то такая РКС будет проводить ток лишь в одном случае, а именно тогда, когда оба переключателя P и Q замкнуты.
В других трех случаях: “ P замкнут и Q разомкнут”, “ P разомкнут и Q замкнут”, “ P замкнут и Q разомкнут” ток со входа А поступать на вход В не будет. А это есть не что иное, как конъюнкция высказываний P, Q, т.е. Аналогичные рассуждения приводят к тому, что параллельная РКС, представленная на рис. 14, является дизъюнкцией
Если высказывание представленная на рис 15, будет проводить ток всегда (какой-либо из контактов будет постоянно замкнут, и ток со входа А будет протекать на выход В либо через верхний контакт, либо через нижний). Такая схема соответствует тождественно истинной формуле.

Тождественно ложной формуле
 
Из схем, приведенных на рис.10 – 16, путем последовательного и параллельного их соединения могут быть построены РКС любой сложности. Обоснованием этого утверждения является то обстоятельство, что любая формула алгебры логики путем равносильных преобразований может быть представлена в одном из базисов: Рассмотрим примеры представления формулы в виде РКС, упрощение этой формулы и последующее представление ее в виде схемы.
Упростим формулу
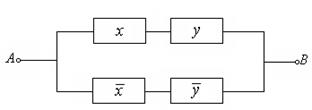
Как нетрудно заметить, последняя РКС значительно проще исходной. В дальнейшем при изображении схем, с целью упрощения их начертания, переменные мы не будем заключать в прямоугольник, а будем их писать в разрыве линий. Тогда, например, предыдущая схема изобразится так:
Рассмотренные РКС, используются главным образом, в устройствах и установках сильноточной техники, т.е. там, где через контакты реле протекают относительно большие токи. Еще большее значение аппарат алгебры логики имеет для элементов и устройств слаботочной техники, т.е. там где протекают малые токи. Такой техникой является микроэлектроника, благодаря достижениям которой созданы современные компьютеры, мобильные телефоны и множество других аппаратов, куда встраиваются микропроцессоры и различного рода цифровые автоматы. Последние же строятся на основе цифровых логических схем, реализуемых в базисах операций Будем считать, что каждая переменная в формуле алгебры логики соответствует одному входу в некоторой логической схеме. Над одной переменной x в алгебре логики, как мы знаем, может выполняться единственная операция отрицания. Для реализации операции отрицания логической схемой необходимо, чтобы эта схема имела один вход x и один выход

Такая схема называется инвертором или схемой НЕ. Она инвертирует сигнал, т.е. переворачивает фазу сигнала на 180 0 (иначе говоря, если мы подадим на вход инвертора сигнала Если в формуле имеется два и более переменных, связанных операцией конъюнкции, то в соответствующей логической схеме мы должны иметь два и более сигнальных входа и один выход, а сама схема будет называться по имени операции, соединяющей эти переменные в формуле. Тогда конъюнкция и дизъюнкция двух переменных в виде схем будут выглядеть так:
   
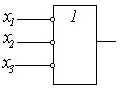
Логическая схема, реализующая операцию конъюнкции, называются схемой совпадения (единичный сигнал на выходе схемы появится лишь тогда, когда оба единичные сигнала на входе совпадут по времени, т.е. оба примут единичное значение), схемой И или конъюнктором. Логическая схема, реализующая операцию дизъюнкции, называется схемой объединения (единичный сигнал на ее выходе появится тогда, когда он появится хотя бы на одном из ее входов), схемой ИЛИ, или дизъюнктором. При числе входов, т.е. переменных, больше двух соответствующие схемы будет отличаться от приведенных выше лишь числом входов и они будут называться соответственно: 2-входовая, 3-входовая и т.д. n -входовая схемы И, 2-входовая, 3-входовая и т.д. n -входовая схемы ИЛИ. Если над некоторым числом переменных, соединенных операцией
Опираясь на приведенное соответствие между формулами алгебры логики и логическими схемами, рассмотрим некоторые примеры перехода от формул к схемам и наоборот. Пример. Представить формулу
Упростим исходную формулу:
Соответствующая этой формуле схема будет иметь вид
При переходе от схемы к формуле её удобно сначала разметить, т.е. обозначить все выходы какими-либо символами (например, большими буквами латинского алфавита A, B, C,…). Затем, двигаясь от последнего выхода к началу, надо последовательно раскрывать каждый символ в соответствии с операциями и теми предшествующими символами, которые используются для получения данного символа. Продвижение по схеме прекращается, когда в формулу будут подставлены только входные переменные. Эту формулу можно затем упростить и по ней построить новую, более простую схему.
Теперь упростим эту формулу:
Упражнения 1.1) Составить РКС, предварительно упростив формулу
3) Упростить РКС
5) Упростить РКС
2. Для ниже приведенных формул составить логические схемы: 1)
1)
3)
4)
Вопросы для самоконтроля 1. Дайте определение высказывания, приведите примеры истинных и ложных высказываний. 2. Запишите таблицу истинности для инверсии, конъюнкции, дизъюнкции, импликации и эквиваленции. 3. Дайте определение тождественно истинной, тождественно ложной и равносильным формулам. 4. Как распределены приоритеты между логическими операциями? 5. Как определяется название сложной формулы? 6. Каков порядок составления таблицы истинности для сложной формулы? 7. Запишите аксиомы и законы алгебры логики. 8. В чем суть полноты систем логических операций? 9. Поясните правила склеивания для элементарных конъюнкций и дизъюнкций. Приведите примеры. 10. Поясните правила поглощения для элементарных конъюнкций и дизъюнкций. Приведите примеры. 11. Поясните правила развертывания для элементарных конъюнкций и дизъюнкций. Приведите примеры. 12. Что такое НДФ, СНДФ, НКФ и СНКФ? 13. Каков вид общей записи любой логической функции в СНДФ? 14. Как записать по таблице истинности логическую функцию в СНДФ? Приведите пример. 15. Каков вид общей записи любой логической функции в СНКФ?
16. Как записать по таблице истинности логическую функцию в СНКФ? Приведите пример. 17. Как осуществляется переход от произвольно заданной логической функции к СНДФ? Приведите пример. 18. Как осуществляется переход от произвольно заданной логической функции к СНКФ? Приведите пример. 19. Перечислите и поясните основные этапы минимизации логических функций, исходя из СНДФ и СНКФ. 20. Расскажите, как осуществляется минимизация логических функций расчетным методом. 21. Как определяется размер карты Карно для общего случая числа переменных в логической функции? 22. Как заполняются клетки карты Карно? 23. Как осуществляется нумерация строки столбцов карты Карно? 24. Каково правило включения клеток карты Карно в покрытие? 25. Как определяется импликанта для каждого покрытия? 26. Поясните суть минимизации логических функций методом Квайна. 27. Поясните, какова связь между логическими функциями и РКС? 28. Поясните, какова связь между логическими функциями и цифровыми логическими семами? 29. Как строятся цифровые схемы по формулам алгебры логики?
Исчисление высказываний Исчислением называют составную часть некоторых разделов математики, трактующих правила вычислений и оперирования с объектами того или иного типа. Например, говорят о дифференциальном, интегральном, вариационном и т.д. исчислениях. В исчислении высказываний объектами исследований являются высказывания. Их исчисление служит для формализации способов логических рассуждений, в которых учитывается лишь логическая структура высказываний, а именно: как одни высказывания получены из других с помощью таких логических операций, как отрицание, конъюнкция дизъюнкция и импликация. Обратим внимание, что сюда не входит операция эквиваленции. В одних литературных источниках данную операцию в этот список включают, в других – нет (например, в математической энциклопедии эта операция в список не включена). В алгебре логики (высказываний) мы под термином “высказывание” понимали любое повествовательное предложение, о котором можно было сказать, истинно оно или ложно. При этом мы испытывали затруднения, когда вставал вопрос о том, считать ли некоторое повествовательное предложение высказыванием, если о его истинности или ложности нельзя было сказать ничего определенного. Поэтому очевидно, что для построения логической теории, которая позволяла бы формализовать процесс получения одних высказываний из других, пользоваться понятиями истинности и ложности нет необходимости. Исчисление высказываний, как раздел математической логики, построено таким образом, что в нем не используются понятия истинности и ложности и не применяются сами законы алгебры логики. Оно является аксиоматической системой. А в основе любой аксиоматической системы лежит совокупность аксиом, с помощью которых, а также определенных правил вывода, получаются новые знания, в частности теоремы.
Возникает вопрос, что такое теорема? Еще со средней школы мы усвоили, что под теоремой понимается всякое утверждение, в истинности которого убеждаются при помощи доказательства. Но теперь встает очередной вопрос: а что такое доказательство? Ответив на этот вопрос, мы ответим и на первый. В современной математике под доказательством понимают конечную последовательность высказываний Отсюда теоремой, или доказуемым высказыванием, называется высказывание, являющееся последним высказыванием некоторого доказательства. Принято считать, что аксиома – это некоторое исходное положение, принимаемое в данной науке без доказательства. Или об аксиоме говорят, что это самоочевидная истина, не требующая доказательства. При таком взгляде на аксиому считается, что её истинность подтверждается многочисленными опытами и практикой. Однако в математической логике считается, что аксиома – это все-таки теорема, причем ее доказательство состоит из одного шага.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.147.190 (0.067 с.) |
 Таким образом, наше высказывание можно представить простейшей РКС (рис.11).
Таким образом, наше высказывание можно представить простейшей РКС (рис.11). или
или Отрицанием высказывания “переключатель Р замкнут” будет высказывание “переключатель Р разомкнут” и этому высказыванию будет соответствовать РКС, представленная на рис.12.
Отрицанием высказывания “переключатель Р замкнут” будет высказывание “переключатель Р разомкнут” и этому высказыванию будет соответствовать РКС, представленная на рис.12.

 .
. .
.
 есть отрицание высказывания P, то РКС,
есть отрицание высказывания P, то РКС,
 , очевидно, будет соответствовать приведенная на рис. 16 РКС
, очевидно, будет соответствовать приведенная на рис. 16 РКС 
 Пример 1.
Пример 1.  .Этой формуле соответствует схема
.Этой формуле соответствует схема Пример 2.
Пример 2.  этой формуле соответствует схема
этой формуле соответствует схема , введя в нее 2 дополнительные конъюнкции
, введя в нее 2 дополнительные конъюнкции  (формула
(формула  от этого не изменится на основании комбинационного закона III.1) и объединив каждую из конъюнкций
от этого не изменится на основании комбинационного закона III.1) и объединив каждую из конъюнкций  со 2, 3 и 4-м членами формулы
со 2, 3 и 4-м членами формулы  Последней формуле будет соответствовать схема
Последней формуле будет соответствовать схема

 , и в виде схемы это будет выглядеть так:
, и в виде схемы это будет выглядеть так:
 , то на его выходе появится сигнал
, то на его выходе появится сигнал  ).
). или
или  , выполняется операция отрицания, то начертание логических схем будет выглядеть так:
, выполняется операция отрицания, то начертание логических схем будет выглядеть так:
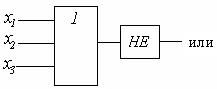




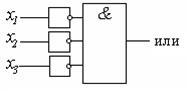 На вход логической схемы могут подаваться уже инвертированные сигналы. Тогда 3-входовые схемы И и ИЛИ будут соответственно такие:
На вход логической схемы могут подаваться уже инвертированные сигналы. Тогда 3-входовые схемы И и ИЛИ будут соответственно такие: в виде логической схемы, упростить эту формулу и нарисовать соответствующую ей схему.
в виде логической схемы, упростить эту формулу и нарисовать соответствующую ей схему. Решение
Решение .
.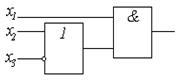
 Пример. Дана схема, для которой нужно записать формулу, упростить ее и построить новую схему.
Пример. Дана схема, для которой нужно записать формулу, упростить ее и построить новую схему.

 Последней конъюнкции соответствует следующая схема:
Последней конъюнкции соответствует следующая схема:
 2) Упростить РКС
2) Упростить РКС
 4) Упростить РКС
4) Упростить РКС
 2)
2)  3)
3)  .
. 3. Для ниже приведенных схем составить формулу, упростить её и по упрощенной формуле составить новую схему:
3. Для ниже приведенных схем составить формулу, упростить её и по упрощенной формуле составить новую схему: 2)
2)

 каждое из которых является либо аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам.
каждое из которых является либо аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам.


