
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные правила выводимости
I. II.
Так как по условию из совокупности формул Н выводима формула С, то существует вывод из Н, последней формулой которого является С:
Если в выводе (1) отсутствует формула С, то он является выводом
только из совокупности Н и, значит, А выводима из H. Если же в выводе (1) одна из формул есть формула С, например формула
Так как в вывод (3) входит вывод (2) из Н, а в оставшуюся часть вывода
Формула С не входит, то вывод (4) является выводом только из Н. На основании же свойства 2 вывода вывод (3) тоже будет выводом только из Н. Поэтому и в этом случае формула А выводима из Н, что и требовалось доказать. Ш. Доказательство. Так как Для правил выводимости II и III можно предложить более простые и компактные доказательства. Докажем правило II, воспользовавшись следующими соображениями. Запись Правило выводимости III доказывается аналогичным образом с той лишь разницей, что здесь не приходится заменять дважды используемое одно и то же множество на одно множество. Заменим в Подобным образом можно доказать также частный случай для правила выводимости III, т.е.
Доказательство. Заменим в IV. Доказательство. Так как из Н выводима формула
Присоединим теперь к совокупности формул Н формулу С. Получим совокупность формул Н, С. Добавляя на основании пункта 1 понятия вывода к выводу (1) формулу С, мы получим вывод
который является выводом из Н, С. Но в конец вывода (2) можно дописать формулу А, которая получается из формул С и
последней формулой которого является формула А. Значит,
V. Ввиду громоздкости доказательства приводить его не будем. Отметим лишь, что теорема дедукции по форме является обратной по отношению к правилу IV. VI. Словесную формулировку этой теоремы можно записать так: если формула А выводима из совокупности формул Доказательство. Обозначим через
По условию,
Опять, используя теорему дедукции, получим
Проделав эту процедуру k раз, мы придем к утверждению
Но из пустого множества выводимы только доказуемые формулы, т.е. VII. Доказательство. По условию
Как было показано ранее (см. подразд. 2.5), из совокупности формул
Используя правило выводимости I, можно записать:
Теперь, используя правило II выводимости, из (4) и (5) получаем
Таким же образом по правилу II из (1) и (6) получаем искомое: VIII. Доказательство. Из условий
Возьмем аксиому
Применяя к формулам (1), (2) и (3) правило сложного заключения, получим
Используя теперь правило выводимости IV, получим
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.172.115 (0.009 с.) |
 .Это правило следует из того простого рассуждения, что если мы можем получить формулу A из совокупности Н, то из расширенной совокупности Н, W мы тем более получим формулу А.
.Это правило следует из того простого рассуждения, что если мы можем получить формулу A из совокупности Н, то из расширенной совокупности Н, W мы тем более получим формулу А. Это почти очевидное правило мы, тем не менее, докажем. Так как по условию из совокупности формул Н, С выводима формула А, то существует вывод из Н, С, последней формулой которого является А:
Это почти очевидное правило мы, тем не менее, докажем. Так как по условию из совокупности формул Н, С выводима формула А, то существует вывод из Н, С, последней формулой которого является А: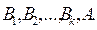 (1)
(1) (2)
(2) , то, вставив между формулами
, то, вставив между формулами  и
и  вывод формулы (2), являющейся выводом из Н, в результате получим вывод из Н, С
вывод формулы (2), являющейся выводом из Н, в результате получим вывод из Н, С (3)
(3) (4)
(4)
 , то по правилу I имеем
, то по правилу I имеем  Так как
Так как  то также по правилу I имеем
то также по правилу I имеем  .
. 

 означает, что для того, чтобы вывести С, нужно иметь совокупность формул Н. Значит, в записи
означает, что для того, чтобы вывести С, нужно иметь совокупность формул Н. Значит, в записи  . Но дважды используемое одно и то же множество Н есть, очевидно, одно множество Н. То есть верна формула
. Но дважды используемое одно и то же множество Н есть, очевидно, одно множество Н. То есть верна формула  , а это и требовалось доказать.
, а это и требовалось доказать.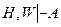 что и требовалось доказать.
что и требовалось доказать.

 множество С на Н, W, тогда
множество С на Н, W, тогда  Но совокупность множеств Н, Н есть одно множество Н, т.е.
Но совокупность множеств Н, Н есть одно множество Н, т.е.  что и требовалось доказать.
что и требовалось доказать.
 , то существует вывод из Н, конечной в котором является формула
, то существует вывод из Н, конечной в котором является формула 
 (1)
(1) (2)
(2) согласно ПЗ (пункт 3) понятия вывода. Отсюда имеем вывод из совокупности Н, С
согласно ПЗ (пункт 3) понятия вывода. Отсюда имеем вывод из совокупности Н, С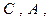
 − теорема дедукции (ТД).
− теорема дедукции (ТД). − обобщенная теорема дедукции (ОТД).
− обобщенная теорема дедукции (ОТД). то доказуема формула
то доказуема формула  .
. совокупность формул
совокупность формул 
 или, что то же самое,
или, что то же самое,  . Но тогда согласно теореме дедукции справедливо утверждение
. Но тогда согласно теореме дедукции справедливо утверждение  . Так как
. Так как  , то справедливо утверждение
, то справедливо утверждение .
.


 – правило введения конъюнкции.
– правило введения конъюнкции. (1)
(1) (2)
(2) выводима конъюнкция
выводима конъюнкция  т.е.
т.е. (3)
(3)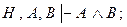 (4)
(4) (5)
(5) (6)
(6) .
. − правило введения дизъюнкции.
− правило введения дизъюнкции.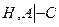 и
и  по теореме дедукции имеем
по теореме дедукции имеем (1)
(1) (2)
(2) . Она выводима из совокупности Н как доказуемая формула, т.е.
. Она выводима из совокупности Н как доказуемая формула, т.е. (3)
(3)
 , что и требовалось доказать.
, что и требовалось доказать.


