
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Снкф для выше приведенной таблицы истинности будут иметь вид
Выше было сказано, что СНДФ и СНКФ являются каноническими, потому что к ним можно свести любую произвольную аналитически заданную логическую функцию. В общем случае переход к СНДФ и СНКФ осуществляется за три шага. 1. Путем многократного применения закона отрицания снимаются групповые и общие отрицания так, что бы они оставались только у одиночных переменных. 2. С помощью распределительных законов производится переход к одной из нормальных форм функций: а) для перехода к НДФ применяется распределительный закон первого рода [раскрываются скобки, т.е. б) для перехода к НКФ применяется распределительный закон второго рода [вводятся скобки, т.е. 3. С помощью правила развертывания производится преобразование членов НДФ или НКФ в соответствующие конституенты. Пример. Преобразовать функцию 1. Применяя законы инверсии, снимаем все групповые отрицания:
Применяя распределительный закон 2-го рода к формуле, полученной после первого шага, будем иметь
3. Применяя правило развертывания, переходим от НДФ к СНДФ и от НКФ к СКНФ:
Упражнения 1. По приведенной ниже таблице истинности составить СНДФ и СНКФ функции
2. Привести функции к СНДФ: 1) 3. Привести функции к СНКФ:
1. 6. Минимизация логических функций Наиболее детально разработаны методы решения канонической задачи минимизации логических функций, которая заключается в отыскании дизъюнктивной (конъюнктивной) формы функции, содержащей минимальной число переменных и операций. Такие формы принято называть минимальными нормальными дизъюнктивными (конъюнктивными) формами.
К настоящему времени разработано достаточно большое число методов и приемов минимизации логических функций. Наиболее известными и распространенными среди них являются: 1) расчетный метод – метод непосредственных логических преобразований; 2) табличный метод – метод карт Карно или Вейча – Карно; 3) расчетно-табличный метод Квайна. Исходной формой для любого из этих методов является одна из совершенных нормальных форм СНДФ или СНКФ. В общем случае любой из упомянутых методов состоит из трех этапов. 1. Переход от СНД(К)Ф к сокращенной сНД(К)Ф путем выполнения всех возможных склеиваний друг с другом сначала конституент, а затем всех членов сумм (произведений) более низкого ранга до тех пор, пока склеивание возможно. Таким образом, под сокращенной формой логической функции будем понимать нормальную дизъюнктивную (конъюнктивную) форму функции, членами которой являются не склеивающиеся друг с другом элементарные конъюнкции (дизъюнкции). Члены сНД(К)Ф носят название простых (или первичных) импликант. Не исключено, что сНД(К)Ф 2. Переход от сНД(К)Ф к тупиковой нормальной дизъюнктивной (конъюнктивной) форме (ТНД(К)Ф) путем устранения избыточных импликант. Под тупиковой будем понимать такую НД(К)Ф логической функции, в которой нет ни одной лишней (избыточной) импликанты. Избыточной будем называть такую импликанту, удаление которой не влияет на значение истинности данной логической функции. Возможны случаи, когда в сНД(К)Ф нет лишних импликант. Тогда сНД(К)Ф Термин тупиковая форма означает, что дальнейшая минимизация путем использования аксиом и законов алгебры логики в рамках нормальных форм уже невозможна. 3. Переход от ТНД(К)Ф к минимальной форме (МНД(К)Ф) логической функции. Этот этап уже не является регулярным, как два предыдущих, поэтому требует определенной сноровки, интуиции и опыта. Здесь имеются в виду поиск возможностей упрощения логической функции методом проб и испытаний. Для уменьшения числа операций отрицания применяют законы де Моргана, а для уменьшения числа конъюнкций и дизъюнкций – распределительные законы.
1. 6. 1. Расчетный метод минимизации Каждый из конкретных методов минимизации состоит из тех же трех шагов, что указывалось выше. Но эти шаги в каждом методе могут иметь свою особенность. 1.Склеивание всевозможных членов исходной СНД(К)Ф, т.е. сначала конституент, затем импликант ранга 2. Проверка каждой простой импликанты в сНД(К)Ф на избыточность с целью её удаления. Проверка состоит в следующем. Так как любая импликанта равна 1 для НДФ (0 для НКФ) лишь на одном наборе переменных, то если на этом наборе сумма остальных членов также обращается в 1 (0), то рассматриваемая импликанта не влияет на значение истинности данной логической функции, т.е. она является избыточной. Удаляя все такие импликанты, получим ТНД(К)Ф. 3. Упрощение полученной ТНД(К)Ф путем применения операции отрицания и распределительного закона 1-го или 2-го рода. Пример. Минимизировать функцию
1. Выполняя склеивание, получим сНД(К)Ф:
2.Удаляем избыточные импликанты: Таким образом, отбросив избыточную импликанту, получим ТНДФ
3. Дальнейшему упрощению функция не поддается. Если исходной является СНКФ, то методика выполнения 1-го шага не меняется. Но реализация 2-го шага имеет свою специфику. На значение истинности функции, представленной в СНКФ, не влияет та импликанта, которая сама равна 0. Но любая импликанта становится нулем только при одном наборе переменных. Следовательно, правило проверки на избыточность можно сформулировать так: · для каждого члена СНКФ определяется набор переменных, которые обращают данный член в 0; · если произведение остальных членов также равно 0, то данный член избыточен. Пример. Получить исходную СНКФ, эквивалентную СНДФ в предыдущем примере, и упростить её. Исходную СНКФ проще всего получить из таблицы истинности, составив ее по СНДФ в предыдущем примере. Упрощенная таблица истинности, т.е. без подробного выписывания всех операций, и соответствующая СНКФ имеют вид:
1. В результате всевозможных склеиваний получаем сНКФ
Дизъюнкция Таким образом, 3. Упрощаем полученную ТНКФ, применив закон де Моргана ко 2-му её члену. В результате получим минимальную форму (МФ)
Это действительно минимальная форма, так как число операций в ТНКФ уменьшилось от 5 до 4 при том же числе переменных 1. 6. 2. Табличный метод минимизации В этом методе два первых шага как бы объединены и выполняются с помощью специальной таблицы, называемой картой Карно (КК) или картой Карно-Вейча (еще иногда называемой диаграммой). Третий шаг выполняется так же, как и в расчетном методе. В принципе карта Карно является разновидностью табличной записи логической функции, заданной в СНДФ или в СНКФ, т.е. представляет разновидность таблицы истинности.
Для двух переменных КК представляет собой квадрат, разделенный на 4 клетки – по одной клетке на каждый набор переменных. Строки этой карты связываются с переменной
скобки указывают, каким переменным соответствуют строки и столбцы карты (рис.1). Если при данном наборе, соответствующем номеру клетки, логическая функция равна 1, то единица записывается в эту клетку. Если логическая функция при данном наборе равна 0, то в клетку записывается 0 (или ничего не записывается). На рис.2 приведена КК с одной заполненной клеткой, и соответствующая этой карте логическая функция будет
значением всего лишь одного разряда (переменной). Для этих целей используется не обычный двоичный код (тогда 3-й и 4-й столбцы на рис.4 были бы соответственно пронумерованы как 10 и 11), а двоичный отраженный код, первая половина которого получается обычным образом, а вторая половина – зеркальным отражением первой, но не всех ее разрядов, а только младших (правых), а в старшем разряде ставится единица. То есть процесс получения отраженных кодов мы можем представить так:
Для 3-разрядных двоичных чисел двоичный отраженный код формируется следующим образом:
Для четырех переменных КК содержит 16 клеток (рис.5).
В карте Карно, изображенной на рис.6, нумерация клеток дается в десятичной системе счисления. Это позволяет производить очень компактную запись логической функции. Действительно, при записи логической функции, можно указать большой знак дизъюнкции Причем число клеток Например, если логическая функция записана в виде
Теперь приведем правила минимизации с помощью КК. 1. 2. Импликанта, соответствующая некоторому покрытию заполненных единицами клеток, содержит символы тех переменных, значения которых совпадают у всех клеток, образующих покрытие. Причем символ берется с отрицанием, если для всех клеток покрытия он принимает значение 0, и без отрицания – в противном случае. Пример. Минимизировать логическую функцию

Рис.8
Следует отметить некоторые особенности работы с покрытиями. Каждое покрытие нужно использовать только один раз. Если КК свернуть в цилиндр вдоль горизонтальной или вертикальной оси, то будет видно, что крайние клетки тоже оказываются соседними и они могут образовывать покрытие. Такой характерный случай покрытий для КК на четыре переменные приведен на рис.9.
Приведем еще один пример КК с отображенной на нее логической функцией, когда единицы находятся в крайних клетках. Эта функция имеет вид
Недостатком рассмотренного метода считается то, что при числе переменных 1.6.3. Расчетно-табличный метод минимизации (метод Квайна) Минимизация этим методом отличается от расчетного только способом выявления избыточных членов в сНДФ. Данный метод предложен американским ученым Квайном, и поэтому называется его именем. Его удобно рассматривать в виде алгоритма с комментариями. Считаем, что минимизируемая логическая функция приведена к СНДФ. 10. Переход от СНДФ к сНДФ. Отыскиваются все простые импликанты. Для этого выписываются все конституенты и все их пары исследуются на возможность склеивания друг с другом. Конституенты, участвующие хотя бы в одном склеивании, отмечаются, но не исключаются из дальнейших сравнений. В результате выявляются импликанты, содержащие по (n-1)-й переменной. С полученными импликантами выполняется та же процедура, что и с исходными конституентами. В результате выявляются импликанты, содержащие n-2 переменные, и так продолжается до тех пор, пока членов, допускающих склеивание, не останется. Все не отмеченные в процессе указанного преобразования члены представляют собой простые импликанты. 20. Переход от сНДФ к ТНДФ. Дизъюнкция всех простых импликант может содержать избыточные импликанты. Поэтому их надо исключить. Для этого составляется импликантная таблица, строки которой обозначаются выявленными на 1-м шаге простыми импликантами, а столбцы – конституентами, входящими в СНДФ исходной функции. 30.Расстановка меток. Любая клетка импликантной таблицы отмечается, например, цифрой 1, если она попадает на пересечение конституенты и импликанты, полностью входящей в конституенту. В каждом столбце при этом может оказаться по нескольку отмеченных клеток. Задача упрощения НДФ сводится к вычеркиванию из таблицы максимального количества строк таким образом, чтобы после этого в каждом столбце осталась, по крайней мере, одна отмеченная клетка.. 40. Выделение ядра Квайна (существенных импликант). Выявляются и вычеркиваются столбцы, содержащие только по одной отмеченной клетке. Простые импликанты, соответствующие этим клеткам, вносятся в окончательное выражение НДФ как обязательные члены. Если таких столбцов нет, то переход к п.50, если же есть, то в таблице зачеркиваются строки, соответствующие обязательным простым импликантам и столбцы, содержащие отмеченные клетки в вычеркнутых строках. 50. Поглощение (сжатие) столбцов. Если после этого в таблице окажутся такие пары столбцов, что все отмеченные клетки i -го столбца совпадают полностью или частично с клетками j- го столбца, то j- й столбец вычеркивается. Если таких пар столбцов нет, то переход к п.70, иначе – к п.60. 60. Вычеркивание пустых строк. Строки, не содержащие после выполнения п.п. 40 и 50 ни одной отмеченной клетки, также вычеркиваются. 70. Поглощение (сжатие) строк. Если в таблице имеется такая пара строк, что все отмеченные клетки k- й строки совпадают полностью или частично с отмеченными клетками l- й строки, то k- я строка вычеркивается. Если таких строк нет, то переход к п.80. 80. Получение МНДФ. Для этого импликанты ядра Квайна, т.е. полученные в п. 40 и оставшиеся не вычеркнутыми после выполнения п. 70, соединяются знаками дизъюнкции. Пример. Минимизировать логическую функцию четырех переменных, заданную в числовой форме
Прочерки в импликантах указывают на отсутствие в них соответствующей переменной. Строим импликантную таблицу (табл.9).
Таблица 9
.
В табл. 9 вертикальные и горизонтальные линии, пересекающие соответствующие столбцы и строки, пронумерованы цифрами. Эти цифры указывают на порядок вычеркивания столбцов и строк. В соответствии с п.40 алгоритма устанавливаем, что импликанты 0–0– и –0–0 являются существенным для конституент 0000,0001,0100,0101 и 0000, 0010,1000,1010. Они должны быть внесены в МНДФ. Поэтому вместе со 2-м и 3-м столбцами, как содержащими всего по одной отмеченной клетке, вычеркиваем 4-ю и 5-ю строки, а также столбцы 1,4,5,7 и 8, на пересечении с которыми в вычеркнутых строках 4 и 5 стоят единицы.
Так как в предыдущей таблице получили строку, не содержащую единиц, то, вычеркивая её, получаем окончательную таблицу:
Соединяя импликанты, соответствующие столбцам с одной отмеченной клеткой и оставшиеся в последней таблице, знаком
Достоинством рассмотренного метода Квайна является то, что он применим для любого числа переменных и может быть реализован в виде программы для ЭВМ. В качестве недостатка можно отметить его относительную сложность. Упражнения 1. Минимизировать расчетным методом логические функции: 1) 2) 3) 4) 2. Упростить с помощью карт Карно функции, заданные в числовой форме: 1) 2)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.8.82 (0.112 с.) |

 .
. ];
]; ;
;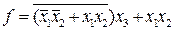 в СНДФ и СНКФ.
в СНДФ и СНКФ. . 2. Применяя распределительный закон 1-го рода, получаем
. 2. Применяя распределительный закон 1-го рода, получаем =
= 






 Переход от одной формы логической функции к другой можно осуществить, используя таблицу истинности. Для этого надо по заданной формуле построить таблицу истинности. Для в всех 1 в столбце функции составить КЕ, соединив их знаком
Переход от одной формы логической функции к другой можно осуществить, используя таблицу истинности. Для этого надо по заданной формуле построить таблицу истинности. Для в всех 1 в столбце функции составить КЕ, соединив их знаком  . Для всех 0 в столбце функции составить КН, заключив их в скобки и поставив между ними знак
. Для всех 0 в столбце функции составить КН, заключив их в скобки и поставив между ними знак  .
.











 ; 2)
; 2)  .
.
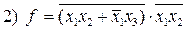 .
. CНД(К)Ф.
CНД(К)Ф. и т.д., пока склеивание возможно.
и т.д., пока склеивание возможно.
 .
. на наборе
на наборе  так как
так как  то импликанта
то импликанта  - избыточная;
- избыточная;  на наборе
на наборе  ;
;  а так как
а так как  , то импликанта
, то импликанта  не является избыточной;
не является избыточной;  на наборе
на наборе  а так как
а так как 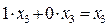 , то импликанта
, то импликанта  не является избыточной.
не является избыточной. .
.

 2. Дизъюнкция
2. Дизъюнкция  при
при 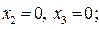 так как
так как  , то импликанта
, то импликанта  – неизбыточна.
– неизбыточна. при
при  ; так как
; так как  , то импликанта
, то импликанта  – избыточна. Дизъюнкция
– избыточна. Дизъюнкция  при
при  ,
,  ; так как
; так как  , то импликанта
, то импликанта 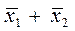 не является избыточной.
не является избыточной.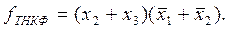

 . Каждая клетка соответствует определенной конституенте, и ей присваивается свой порядковый номер, который представляет собой двоичное число, в разрядах которого записываются цифры (набор), находящиеся слева от клетки и сверху над ней. Фигурные
. Каждая клетка соответствует определенной конституенте, и ей присваивается свой порядковый номер, который представляет собой двоичное число, в разрядах которого записываются цифры (набор), находящиеся слева от клетки и сверху над ней. Фигурные
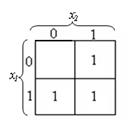




 . На рис.3 приведена карта с тремя заполненными клетками, и ей будет соответствовать функция
. На рис.3 приведена карта с тремя заполненными клетками, и ей будет соответствовать функция  т.е. конституенты, соответствующие заполненным клеткам в функции, соединяются дизъюнкцией.
т.е. конституенты, соответствующие заполненным клеткам в функции, соединяются дизъюнкцией. В случае трех переменных КК содержит 8 клеток, и нумеруются они так, как показано на рис.4. Номер каждой клетки получается объединением всех цифр, находящихся слева от клетки и сверху от нее.
В случае трех переменных КК содержит 8 клеток, и нумеруются они так, как показано на рис.4. Номер каждой клетки получается объединением всех цифр, находящихся слева от клетки и сверху от нее.


 Для пяти переменных необходимо иметь КК с 32 клетками. Эти 32 клетки можно представить как 2 карты по 16 клеток или одну карту на 32 клетки. Одна карта на 32 клетки будет иметь такую нумерацию строк и столбцов с учетом использования отраженных кодов, которая показана на рис.6.
Для пяти переменных необходимо иметь КК с 32 клетками. Эти 32 клетки можно представить как 2 карты по 16 клеток или одну карту на 32 клетки. Одна карта на 32 клетки будет иметь такую нумерацию строк и столбцов с учетом использования отраженных кодов, которая показана на рис.6.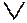 (применяемый аналогично знаку
(применяемый аналогично знаку  или
или  в обычной алгебре), в скобках после него перечислить те номера клеток, в которые должна быть помещена 1. Такую запись логической функции называют числовой.
в обычной алгебре), в скобках после него перечислить те номера клеток, в которые должна быть помещена 1. Такую запись логической функции называют числовой. в КК зависит от числа переменных m и будет определяться по максимальному номеру клетки как
в КК зависит от числа переменных m и будет определяться по максимальному номеру клетки как  , где
, где  − ближайшая наибольшая целая часть
− ближайшая наибольшая целая часть  , т.е.
, т.е.  , а
, а  − максимальный номер клетки в такой записи.
− максимальный номер клетки в такой записи. то это значит, что число клеток будет
то это значит, что число клеток будет  т.е. число переменных будет 4, число клеток будет
т.е. число переменных будет 4, число клеток будет  а единицы надо поместить в клетки с номерами 0,1,3,4,6,9,11. В двоичной системе счисления эти номера будут иметь вид: 0000,0001,0011,0100,0110,1001,1011. Тогда КК с отображенной на нее приведенной функцией будет иметь вид, представленный на рис.7.
а единицы надо поместить в клетки с номерами 0,1,3,4,6,9,11. В двоичной системе счисления эти номера будут иметь вид: 0000,0001,0011,0100,0110,1001,1011. Тогда КК с отображенной на нее приведенной функцией будет иметь вид, представленный на рис.7.
 соседних клеток, содержащих 1, и расположенных по вертикали либо по горизонтали в виде прямоугольника либо квадрата (такую совокупность клеток называют покрытием), соответствуют одной импликанте, ранг которой
соседних клеток, содержащих 1, и расположенных по вертикали либо по горизонтали в виде прямоугольника либо квадрата (такую совокупность клеток называют покрытием), соответствуют одной импликанте, ранг которой  где
где  − число переменных, меньше ранга покрываемых конституент на
− число переменных, меньше ранга покрываемых конституент на  единиц. Чем больше клеток в покрытии, тем проще выражаемый этим покрытием член логической функции − импликанта.
единиц. Чем больше клеток в покрытии, тем проще выражаемый этим покрытием член логической функции − импликанта. с помощью КК. Минимизируемая функция будет состоять из трех переменных, соответствующая ей КК будет состоять из 8 клеток. Поэтому КК, с отображенной на нее заданной функцией в виде помеченных единицами клеток и выделенных пунктирными линиями покрытий, приведена на рис.8.
с помощью КК. Минимизируемая функция будет состоять из трех переменных, соответствующая ей КК будет состоять из 8 клеток. Поэтому КК, с отображенной на нее заданной функцией в виде помеченных единицами клеток и выделенных пунктирными линиями покрытий, приведена на рис.8.



 . Соответствующая ей КК приведена на рис.10.
. Соответствующая ей КК приведена на рис.10.



 КК становятся громоздкими и неудобными для практического применения. Однако, справедливости ради, нужно отметить, что сейчас уже имеются разработанные компьютерные программы, минимизирующие логические функции с 9 переменными.
КК становятся громоздкими и неудобными для практического применения. Однако, справедливости ради, нужно отметить, что сейчас уже имеются разработанные компьютерные программы, минимизирующие логические функции с 9 переменными. . Так как наша цель – рассмотрение процесса преобразования импликантной таблицы, то п. 10 алгоритма выполнять не будем, а выпишем готовые импликанты. Их совокупность будет иметь вид
. Так как наша цель – рассмотрение процесса преобразования импликантной таблицы, то п. 10 алгоритма выполнять не будем, а выпишем готовые импликанты. Их совокупность будет иметь вид .
.
 В результате выполнения этих операций импликантная таблица приобретает вид:
В результате выполнения этих операций импликантная таблица приобретает вид: Далее выполняем поглощение столбцов. Однако это невозможно, так как в таблице нет ни одной пары столбцов, которые бы полностью или частично совпадали. Поэтому в соответствии с п.70 алгоритма выполняем поглощение строк. Видим, что строка 2 поглощает строку 1, а строка 5 – строку 4. В результате получаем таблицу:
Далее выполняем поглощение столбцов. Однако это невозможно, так как в таблице нет ни одной пары столбцов, которые бы полностью или частично совпадали. Поэтому в соответствии с п.70 алгоритма выполняем поглощение строк. Видим, что строка 2 поглощает строку 1, а строка 5 – строку 4. В результате получаем таблицу: Снова выполняем поглощение столбцов и получаем таблицу:
Снова выполняем поглощение столбцов и получаем таблицу:
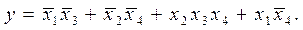
 ;
; ;
; ;
; .
.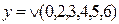 ; 2)
; 2) 
 ; 4)
; 4) 



