
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о верхней и нижней гранях множеств
При рассмотрении числовых множеств часто возникает необходимость установления их граничных значений. Если множество задано перечислением его элементов, то это делается без особого труда путем выделения его минимального и максимального значений. Например, для множества X = {0, 1, 2, 4, 8} min x = 0, max x = 8. Если же множество задано в «форме от х», то указать минимальное и максимальное его значения не всегда оказывается просто, а иногда они и не существуют. Например, для множества N натуральных чисел минимальным числом является единица. А максимальное число не существует. Для множества Z целых чисел не существует ни минимума, ни максимума. В подобных случаях используют понятия верхней и нижней граней множества (иногда говорят о верхней и нижней границах). Рассмотрим эти понятия более подробно. Пусть задано некоторое множество X действительных чисел. Число а называется его верхней гранью и обозначается sup X (от лат. supremum – наивысшее), если для любого числа х Для рассмотренного выше множества X ={0, 1, 2, 4, 8} очевидно, что min X = inf X = 0, max X = sup X = 8. Однако для неограниченного сверху множества N натуральных чисел min N = inf N = 1, а max N не существует, но sup N = + Приведенные примеры возможно не очень убедительны, так как использование символов –
Например, для отрезка 1 ≤ х ≤ 3 при х Чисел, которые могут рассматриваться в качестве верхней или нижней граней множества, может быть бесконечно много. Для устранения такой неоднозначности введено понятие точной верхней и точной нижней граней множества. Под точной верхней гранью множества Х понимают такую верхнюю грань, которая не превосходит любую другую. Под точной нижней гранью множества Х, понимают такую нижнюю грань, которая не меньше любой другой грани. Исходя из приведенных определений, символически точные верхние и нижние грани множества, если его представлять в виде последовательности действительных чисел, можно записать через верхний и нижний пределы: для бесконечных множеств. Однако чтобы не перегружать символикой понятия точной верхней и нижней граней пределы опускают и в качестве точной верхней и нижней граней принимают соответственно sup X и inf X. Наконец, следует отметить, что всякое непустое множество действительных чисел имеет, и притом единственную, верхнюю и нижнюю конечную или бесконечную грани. Операции над множествами.
Над множествами можно выполнять определенные операции, подобные в некотором отношении операциям над действительными числами в алгебре. Поэтому можно говорить об алгебре множеств. Объединением (соединением) множеств А и В называется множество (символически оно обозначается через
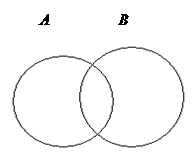
Запись Операции над множествами наглядно изображают графически с помощью кругов Эйлера (иногда используют термин «диаграммы Венна-Эйлера»). Если все элементы множества А будут сосредоточены в пределах круга А, а элементы множества В – в пределах круга В, тооперацию объединения с помощью кругов Эйлера можно представить в следующем виде – рис. 2.1
Рис. 2.1. Объединение множеств А и В
Пример 1. Объединением множества А = {0, 2, 4, 6, 8} четных цифр и множества В = {1, 3, 5, 7, 9} нечетных цифр является множество Пример 2. Если A = {1, 2, 3}, B = {2, 3, 4}, то Пример 3. Объединением множеств А = {1} и B = {0, 1} решений квадратных уравнений х 2 + 2 х + 1 = 0 и х 2 + х = 0 является множество В общем случае в операции объединения может участвовать n множеств А 1, А 2, …, А n. Тогда объединением этих множеств (обозначается через Пример 4. Пусть А 1 = {3,6,9}, A 2 = {0,1,5,7}, A 3= {2,3,4,5,8}, тогда Пересечением (произведением) множеств А и В называется множество (обозначается через В форме от х пересечение множеств записывается так
Запись
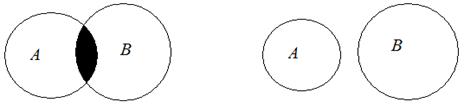
а б Рис. 2.2. Пересечение множеств А и В
Если Аналогично операции объединения в пересечении может участвовать n множеств А 1, А 2, …, А n. Тогда пересечением этих множеств (обозначается через Пример 5. Пусть А 1 = {1, 2, 3, 4, 8}, A 2 = {2, 3, 4, 5, 8}, A 3= {3, 6, 7,8, 9}, тогда
Разностью множеств А и В называется множество (обозначается А \ В или А – В), состоящее из всех тех элементов множества А, которые не являются элементами множества В. В «форме от х» разность множеств А и В можно записать так
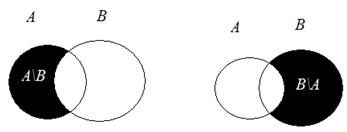
Выражение А \ В читается: «разность А и В» или «А без В». Разность множеств в отличие от предыдущих операций определяется только для двух множеств. С помощью кругов Эйлера для множеств А и В разности А \ В и В\А в виде затемненных частей кругов приведены соответственно на рис. 2.3 а, и 2.3 б
а б Рис. 2.3. Разности множеств А \ В и В\А
Пример 6. Пусть А = {0, 2, 4, 6, 8} – множество всех четных цифр, В = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – множество всех цифр десятичной системы счисления. Тогда В\А = {1, 3, 5, 7, 9} всех нечетных цифр является разностью множеств В и А. Пример 7. Пусть A = {1, 2, 3, 4}, B = {1, 3, 5}, C = {5, 6, 7}. Тогда А \ В = = {2, 4}, А \ С = {1, 2, 3, 4} = A, C \ A = {5, 6, 7} = C, В\С = {1, 3}, C \ В = {6, 7}, В\А = {5}. Для случая, когда Дополнением множества А до множества В называется множество, всех тех элементов множества В, которые не принадлежат множеству А. С помощью кругов Эйлера множество-дополнение в затемненном виде представлено на рис. 2.4
Рис. 2.4. Подмножество В\A – дополнение множества А до множества В Символически операция дополнения записывается также как и операция разности, поэтому в «форме от х»запись дополнения будет иметь вид
Если в процессе некоторого рассуждения все рассматриваемые множества являются подмножествами некоторого множества U, то это множество называют универсальным множеством (или для краткости – универсумом). Рассуждение может быть не только кратким, но и представлять научную теорию или целую книгу. Например, при проведении социологических исследований в качестве универсума могут рассматриваться все города России или все студенты некоторого вуза. В первом случае все рассуждения не могут выходить за рамки всех городов, а во втором – за рамки всех студентов этого вуза. Для графической иллюстрации отношений между подмножествами какого-либо ограниченного универсального множества U круги Эйлера, отображающие подмножества множества U, ограничивают прямоугольником – рис. 2.5
Рис. 2.5. Универсальное множество U и его подмножества A и B Ясно, что если в некотором рассуждении универсальное множество будет неограниченным, например множество N или Z,то ограничить его прямоугольником не представляется возможным. Если в рассуждениях участвуют универсальное множество U и некоторое подмножество A, то подмножество
Тогда приведенное выше определение дополнения множества A до множества B называют относительным. Кроме приведенных операций над множествами рассматривают еще две – операцию симметрической разности и операцию сложения множеств. Симметрической разностью (обозначается
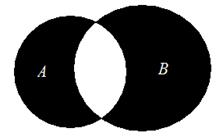
С помощью кругов Эйлера симметрическая разность множества А (левый полный круг)и множества В (правый полный круг)на рис. 2.6 будет представлять затемненную часть
Рис. 2.6. Симметрическая разность множеств А и В Суммой множеств А и В (обозначается А + В) называется множество, определяемое выражением А + В = ( Исходя из приведенной записи для операции сложения, можно сказать, что сумма множеств равна их объединению без пересечения. Симметрическая разность множеств А и В и их сумма представляют одно и то же множество. Покажем это, используя круги Эйлера.
По определению разность множеств А и В или относительное дополнение А \ В являются подмножеством, изображенным на рис. 2.7 а (на рис. 2.3 а это левая затемненная часть круга Эйлера). Разность множеств В и А или относительное дополнение В\A является подмножеством, изображенным на рис. 2.7 б (на рис. 2.3 б это правая затемненная часть круга Эйлера)
а б Рис. 2.7. Подмножества А \ В и В\А Объединяя эти подмножества, мы получаем фигуру, приведенную на рис. 2.6, которая представляет по определению симметрическую разность множеств А и В, т.е. С другой стороны, если мы объединим множества А и В, то получим правую фигуру, т.е. Таким образом, мы доказали с помощью кругов Эйлера, что
Рассмотрим примеры выполнения операций вычитания, дополнения, сложения и симметрической разности для различных случаев задания множеств. Пример 8. Пусть заданы множества: А = {2, 3}; B = {1, 2, 3, 4, 5}; C = = {1, 2, 3}; D = {3, 4, 5}. Тогда А \ В = Æ; А \ С = Æ; А \ D = {2}; A \ A = Æ; B \ A = {1, 4, 5}; B \ C = {4, 5}; B \ D = {1, 2}; C \ A = {1}; C \ B = Æ; C \ D = {1, 2}; D \ A = {4, 5}; D \ B = Æ; D \ C = {4, 5}. А + В ={1, 2, 3, 4, 5}\{2, 3}={1, 4, 5}; B + A ={1, 2, 3, 4, 5}\{2, 3}={1, 4, 5}.
A + C = {1, 2, 3}\{2, 3} = {1}; C + A = {1, 2, 3}\{2, 3} = {1}.
A + D = {2, 3, 4, 5}\{3} = {2, 4, 5}; D + A= {2, 3, 4, 5}\{3} = {2, 4, 5}.
B + C = {1, 2, 3, 4, 5}\{1, 2, 3} = {4, 5}; C + B = {4, 5}.
В + D = {1, 2, 3, 4, 5}\{3, 4, 5} = {1, 2}; D + B = {1, 2}.
C + D = {1, 2, 3, 4, 5}\{3} = {1, 2, 4, 5}; D + C = {1, 2, 4, 5}.
Из приведенных примеров видно, что операции сложения и симметрической разности эквивалентны и обладают свойством коммутативности.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 41009; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.238.76 (0.055 с.) |
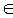 Х выполняется неравенство
Х выполняется неравенство  и, каково бы ни было число а ʹ < а, существует такое число х ʹ
и, каково бы ни было число а ʹ < а, существует такое число х ʹ 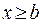 и, каково бы ни было число b ʹ > b, существует такое х ʹ
и, каково бы ни было число b ʹ > b, существует такое х ʹ 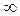 . В этом и состоит различие между минимальным значением и инфимумом, а также между максимальным значением и супремумом некоторого множества Х. Если будем рассматривать множество Z, то ни минимального, ни максимального его значений не существует, но inf Z = –
. В этом и состоит различие между минимальным значением и инфимумом, а также между максимальным значением и супремумом некоторого множества Х. Если будем рассматривать множество Z, то ни минимального, ни максимального его значений не существует, но inf Z = – 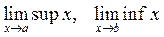 для конечных множеств и
для конечных множеств и 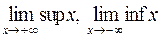
 ), состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В. В форме от х объединение множеств записывается так
), состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В. В форме от х объединение множеств записывается так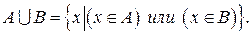

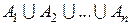 или
или 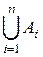 ), будет множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А 1, А 2,..., Аn.
), будет множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А 1, А 2,..., Аn.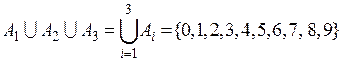 .
.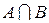 , иногда А × В или АВ), состоящее из всех тех элементов, которые принадлежат каждому из множеств А и В.
, иногда А × В или АВ), состоящее из всех тех элементов, которые принадлежат каждому из множеств А и В.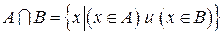 .
.
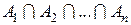 или
или 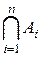 ), будет множество, состоящее из всех тех элементов, которые принадлежат одновременно всем множествам А 1, А 2,..., Аn.
), будет множество, состоящее из всех тех элементов, которые принадлежат одновременно всем множествам А 1, А 2,..., Аn.
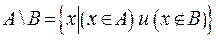 .
.
 определяют операцию дополнения множества А до множества В.
определяют операцию дополнения множества А до множества В.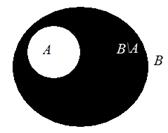
 .
.

 всех тех элементов множества U, которые не принадлежат подмножеству А, называется абсолютным дополнением подмножества А до множества U. Ясно, что
всех тех элементов множества U, которые не принадлежат подмножеству А, называется абсолютным дополнением подмножества А до множества U. Ясно, что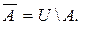
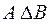 ) называется множество, определяемое следующим образом:
) называется множество, определяемое следующим образом: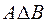 =
= 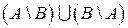 .
.
 )\
)\  .
.
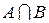 , представленное на рис. 2.2 а, то снова получим фигуру, изображенную на рис. 2.6. Но это и есть объединение множеств А и В без их пересечения, т.е. сумма А + В.
, представленное на рис. 2.2 а, то снова получим фигуру, изображенную на рис. 2.6. Но это и есть объединение множеств А и В без их пересечения, т.е. сумма А + В. {1, 4, 5}= {1, 4, 5};
{1, 4, 5}= {1, 4, 5};  = {1, 4, 5}
= {1, 4, 5} 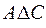 = Æ
= Æ  = {1}
= {1} 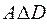 = {2}
= {2} 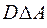 = {4, 5}
= {4, 5} 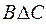 = {4, 5}
= {4, 5} 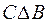 = {4, 5}.
= {4, 5}.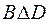 = {1, 2}
= {1, 2}  = {1, 2}.
= {1, 2}.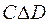 = {1, 2}
= {1, 2} 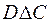 = {1, 2, 4, 5}.
= {1, 2, 4, 5}.


