
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблемы аксиоматического исчисления высказываний
Всякая аксиоматическая теория для своего обоснования требует рассмотренных четырех проблем: 1) проблемы разрешимости, 2) проблемы непротиворечивости, 3) проблемы полноты, 4) проблемы независимости. Раскроем эти проблемы чуть детальнее, сформулировав их в виде теорем, но, не приводя соответствующего доказательства. 1. Проблема разрешимости исчисления высказываний заключается в доказательстве существования алгоритма, который позволил бы для любой заданной формулы исчисления высказываний определить, является она доказуемой или нет. Теорема 1. Проблема разрешимости для исчисления высказываний разрешима. 2. Суть проблемы непротиворечивости исчисления высказываний состоит в следующем. Логическое исчисление называется непротиворечивым, если в нем недоказуемы никакие две формулы, из которых одна является отрицанием другой. Иначе говоря, аксиоматическое исчисление называется непротиворечивым, если в нем не существует такая доказуемая формула А, что наряду с ней доказуема и формула Теорема 2. Исчисление высказываний непротиворечиво. 3. Проблема полноты исчисления высказываний. Существует два понятия полноты − в узком смысле и в широком смысле. Аксиоматическое исчисление называется полным в узком смысле, если добавление к списку его аксиом любой недоказуемой в исчислении формулы в качестве новой аксиомы приводит к противоречивому исчислению. Исчисление высказываний называется полным в широком смысле, если любая тождественно истинная формула в алгебре логики доказуема в исчислении высказываний. Теорема 3. Исчисление высказываний полно в узком смысле. Теорема 4. Исчисление высказываний полно в широком смысле. 4. Проблема независимости аксиом исчисления высказываний. Для каждого аксиоматического исчисления возникает вопрос о независимости его аксиом; а именно: нельзя ли какую-нибудь аксиому вывести из остальных аксиом, применяя правила вывода? Если для некоторой аксиомы это возможно, то ее можно исключить из списка аксиом системы, и возможности логического исчисления при этом не изменятся. Иначе говоря, класс доказуемых формул не изменится. Аксиома называется независимой от всех остальных аксиом исчисления, если она не может быть выведена из остальных аксиом.
Система аксиом исчисления высказываний называется независимой, если каждая аксиома системы независима. Теорема 5. Система аксиом исчисления высказываний независима. Из описания проблем исчисления высказываний вытекает вопрос: а не существует ли между алгеброй логики и исчислением высказываний такая связь, которая позволила бы некоторые проблемы исчисления высказываний решить с помощью алгебры логики, и наоборот. Такая связь существует и на такую связь, в первую очередь, указывает теорема 4 о полноте исчисления высказываний в широком смысле. Используя эту теорему, можно установить доказуемость любой формулы путем установления ее тождественной истинности в алгебре логики. Такую замену выгодно осуществлять тогда, когда непосредственное установление доказуемости проблематично. Существует и обратная теорема о том, что каждая формула, доказуемая в исчислении высказываний, является тождественно истинной в алгебре логики. Эту теорему можно применять в тех случаях, когда установление тождественной истинности формулы (ТИФ) заменяют установлением ее доказуемости. О тесной взаимосвязи ТИФ и доказуемых формул свидетельствует тот факт, что часто в математической логике тождественная истинность формулы обозначается символом Таким образом, прямую и обратную теоремы о полноте в широком смысле кратко можно записать так:
Несмотря на то, что из теоремы 4 следует, что все аксиомы исчисления высказываний являются ТИФ алгебры логики, мы, тем не менее, это проверим. Проверку проведем, представляя каждую аксиому исчисления высказываний как соответствующую формулу алгебры логики и выполняя ее алгебраические преобразования в соответствии с аксиомами и законами алгебры логики. При этом анализировать аксиомы будем не в том порядке, как они записаны в подразд. 2.2, а в порядке увеличения сложности их анализа. Как правило, анализ “коротких” аксиом является менее громоздким, чем анализ “длинных” аксиом.
1) I1: 2) II1: 3) II2: 4) III1: 5) III2: 6) IV2: 7) IV3: 8)IV1: 9) I2:
10) II3:
11) III
Таким образом, все 11 аксиом являются ТИФ в алгебре логики. В качестве аксиом могут быть выбраны и другие формулы. Так, известна и другая система из 10 аксиом, которая приводится ниже. Для различения аксиом этой системы и аксиом, рассмотренных выше, будем обозначать их так:
Покажем, что аксиомы этой системы являются также ТИФ алгебры логики. Действительно, аксиомы Сделаем это:
Последняя формула точно совпадает с третьей формулой для последовательности равносильных формул в I2. Ее последующие преобразования показали, что она ТИФ. Следовательно, не продолжая дальнейшие преобразования, мы можем заключить, что Видим, что все аксиомы этой системы также являются ТИФ алгебры логики. Использованием теоремы 4 о полноте исчисления высказываний в широком смысле может значительно упроститься процесс установления доказуемости формул. Действительно, тогда вместо того, чтобы искать некоторый вывод из совокупности формул, а затем по обобщенной теореме дедукции устанавливать доказуемость анализируемой исходной формулы, достаточно установить, является она ТИФ (общезначимой) или нет. Процесс же установления общезначимости формулы более определен, чем процесс установления доказуемости формул. Действительно, если установление общезначимости формулы путем алгебраических преобразований вызывает затруднения, то всегда для любой формулы можно построить таблицу истинности и по ней определить, является она общезначимой или нет (напомним, что формула будет общезначимой, если в последнем столбце её таблицы истинности будут стоять все единицы). Наконец, последний штрих данного раздела. Как мы видим из предыдущих рассуждений, некоторые проблемы, трудно разрешимые в исчислении высказываний, достаточно просто могут быть решены в алгебре логики. Очевидно, таких проблем может быть множество. Поэтому говорят, что алгебра логики является интерпретацией (интерпретирует – растолковывает, разъясняет) исчисления высказываний. И вообще, относительно более абстрактная (сложная, развитая, общая) теория интерпретируется теорией менее абстрактной.
Вопросы для самоконтроля 1. Какая запись является формулой в исчислении высказываний? 2. Запишите аксиомы исчисления высказываний. 3. Сформулируйте правило подстановки и правило одновременной подстановки. 4. Сформулируйте правило заключения и правило сложного заключения. 5. Что понимается под термином «доказуемость» в исчислении высказываний. Дайте определение доказуемой формулы. 6. Сформулируйте и запишите правило силлогизма. 7. Сформулируйте и запишите правило контропозиции. 8. Сформулируйте и запишите правило снятия двойного отрицания. 9. Дайте определение выводимо формулы. 10. Что называется выводом из совокупности формул H?
11. Сформулируйте и запишите теорему дедукции. 12. Запишите обобщенную теорему дедукции и приведите ее доказательство. 13. Запишите правило введения конъюнкции. 14. Запишите правило введения дизъюнкции. 15. Перечислите четыре основных проблемы исчисления высказываний и прокомментируйте их. 16. Докажите тождественную истинность аксиомы I2. 17. Докажите тождественную истинность аксиомы II3. 18. Докажите тождественную истинность аксиомы III3. 19. Докажите тождественную истинность аксиомы IV4.
Логика предикатов Понятие предиката Как отмечалось в вводной части предыдущего раздела, основным предназначением исчисления высказываний является формализация способов логических рассуждений, позволяющих в компактной форме из одних высказываний получать другие, используя определенные логические операции. При этом учитывается лишь структура связей между высказываниями и совершенно игнорируется смысловое содержание самих высказываний. Другими словами, исчисление высказываний рассматривает каждое высказывание как единое целое, не разделяя его на составные части – подлежащее и сказуемое, как это делается в грамматике естественного, например русского, языка. Часто это приводит к тому, что участвующие в логических операциях высказывания по смыслу могут быть совершенно не связанными между собой, и, тем не менее, полученные из них новые сложные высказывания будут правильными с точки зрения исчисления высказываний, хотя и абсурдными с точки зрения естественного языка. Так, например, высказывание “если число 15 делится на 3, то каждый день начинается с восхода солнца” является законным с точки зрения исчисления высказываний, но абсурдным с точки зрения естественного языка, так как составляющие его простые высказывания никак не связаны по смыслу (по содержанию). В то же время в науке и практике существуют такие заключения, которые существенным образом зависят не только от структуры, но и от содержания используемых в них высказываний. Например, из двух высказываний “всякая дифференцируемая функция является непрерывной” и “функция
Это говорит о том, что изобразительные средства исчисления высказываний недостаточны для того, чтобы делать подобные заключения. Символика исчисления высказываний бедна и не позволяет выражать смысловое содержание высказываний. Значительно большими возможностями обладает другая логическая теория – алгебра предикатов и соответственно исчисление предикатов (всё вместе взятое называют логикой предикатов). В логику предикатов алгебра логики (алгебра высказываний) и исчисление высказываний входят как составные части. Поэтому все законы алгебры логики и исчисления высказываний действуют в логике предикатов. К тому же, мы вновь возвращаем высказываниям понятия истинности и ложности. Логика предикатов расчленяет простое высказывание на субъект (подлежащее, дополнение) и предикат (сказуемое, определение). Субъект – это то, о чем что-то утверждается в высказывании. Предикат – это то, что именно утверждается о субъекте. Например, в высказывании “12 – составное число” “12” – субъект, “ составное число” – предикат. Это высказывание утверждает, что “12” обладает свойством быть составным числом. Если в приведенном примере заменить конкретное число 12 переменной Вместе с тем, если переменной Из изложенного выше вытекают следующие определения. Определение 1. Одноместным предикатом Множество Множество всех элементов Так, предикат Другой предикат
Нетрудно заметить, что приведенные примеры одноместных предикатов выражают свойства предметов. Определение 2. Предикат Обобщением понятия одноместного предиката является понятие Здесь множество Определение 3. Двухместным предикатом
Таким образом, предикат – это функция или, как мы уже говорили выше, высказывательная форма. Если, например, в высказывательную форму Еще несколько замечаний о терминологии. Иногда вместо термина “ Для общности еще вводят понятие 0 -арного предиката, под которым понимается любое истинное или ложное высказывание. Такое определение логично, если вспомнить, что в определении высказывания нет переменной, а в определении предиката она есть. Тогда некоторое предложение мы можем называть 0-арным предикатом, если в нем отсутствуют переменные.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1680; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.183 (0.058 с.) |
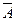 .
. (ранее в подразд.1.3 для этой цели мы использовали запись
(ранее в подразд.1.3 для этой цели мы использовали запись  ), по своему начертанию очень похожим на символ доказуемой формулы
), по своему начертанию очень похожим на символ доказуемой формулы  . Тождественно истинную формулу еще называют общезначимой или логическим законом.
. Тождественно истинную формулу еще называют общезначимой или логическим законом. следует
следует  ,т.е. получаем
,т.е. получаем  т.е.
т.е.  т.е.
т.е.  , т.е.
, т.е.  ,т.е.
,т.е.  , т.е.
, т.е. 
 , т.е.
, т.е. 
 т.е.
т.е. 


 т.е.
т.е. 
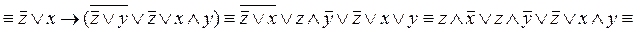


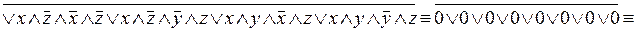
 , т.е.
, т.е.  .
. 


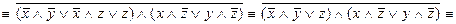
 т.е
т.е 


 ;
;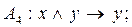

 ;
;



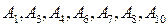 совпадают с аксиомами
совпадают с аксиомами  соответственно. Тождественную истинность последних мы уже доказали выше, значит, аксиомы
соответственно. Тождественную истинность последних мы уже доказали выше, значит, аксиомы  и
и  .
.
 т.е.
т.е. 
 [
[  ]
] 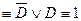 ,т.е.
,т.е. 


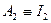 и тоже является ТИФ.
и тоже является ТИФ. является дифференцируемой” средствами исчисления высказываний нельзя вывести третье высказывание “функция
является дифференцируемой” средствами исчисления высказываний нельзя вывести третье высказывание “функция  из множества натуральных чисел, то получим так называемую высказывательную форму: “
из множества натуральных чисел, то получим так называемую высказывательную форму: “ 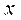 –составное число”. Обратим внимание, что в данном примере при замене числа 12 на
–составное число”. Обратим внимание, что в данном примере при замене числа 12 на  ,
,  то эта высказывательная форма даст ложные высказывания, а при других значениях
то эта высказывательная форма даст ложные высказывания, а при других значениях  ,
,  ) эта форма даст истинные высказывания. Отсюда ясно, что эта высказывательная форма является функцией одной переменной
) эта форма даст истинные высказывания. Отсюда ясно, что эта высказывательная форма является функцией одной переменной  , т.е. значения истины или лжи.
, т.е. значения истины или лжи. называется произвольная функция переменной
называется произвольная функция переменной 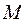 и принимающая значения из множества
и принимающая значения из множества 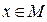 , при которых предикат
, при которых предикат 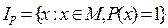 . Эта запись означает, что множество
. Эта запись означает, что множество  состоит из элементов, обладающих свойством, указанным после двоеточия.
состоит из элементов, обладающих свойством, указанным после двоеточия.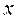 – составное число” определен на множестве
– составное число” определен на множестве 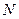 (всех натуральных чисел), а множество
(всех натуральных чисел), а множество 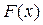 − “диагонали параллелограмма
− “диагонали параллелограмма  , называется тождественно истинным (тождественно ложным), если
, называется тождественно истинным (тождественно ложным), если  .
.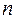 -местного предиката, с помощью которого выражается отношение между
-местного предиката, с помощью которого выражается отношение между  предметами. Так, примером бинарного отношения (отношение между двумя предметами) является отношение “меньше”. Пусть это отношение рассматривается на множестве
предметами. Так, примером бинарного отношения (отношение между двумя предметами) является отношение “меньше”. Пусть это отношение рассматривается на множестве 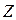 целых чисел. Тогда оно может быть охарактеризовано высказывательной формой “
целых чисел. Тогда оно может быть охарактеризовано высказывательной формой “ 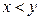 ”, где
”, где  , т.е. является функцией двух переменных
, т.е. является функцией двух переменных  , определенной на множестве
, определенной на множестве  с множеством значений
с множеством значений  .
. и
и 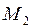 .
.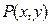 называется функция двух переменных
называется функция двух переменных  , определенная на множестве
, определенная на множестве 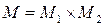 и принимающая значение из множества
и принимающая значение из множества  ─ “
─ “ 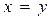 ”, определенный на множестве действительных чисел
”, определенный на множестве действительных чисел  , предикат делимости нацело
, предикат делимости нацело 
 ”
”  ”, определенный на множестве
”, определенный на множестве  .
. мы подставим вместо
мы подставим вместо  есть предикат (высказывательная форма), но
есть предикат (высказывательная форма), но 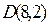 уже является истинным высказыванием, а
уже является истинным высказыванием, а  − ложным высказыванием. В то же время
− ложным высказыванием. В то же время  является высказывательной формой (предикатом), так как его значение истинности зависит от того, каким натуральным числом будет заменена переменная
является высказывательной формой (предикатом), так как его значение истинности зависит от того, каким натуральным числом будет заменена переменная  является высказыванием, причем истинным, так как любое
является высказыванием, причем истинным, так как любое  делится на единицу.
делится на единицу. этот предикат называется унарным (от лат. unio ─ единение, единый), при
этот предикат называется унарным (от лат. unio ─ единение, единый), при  − бинарным (от лат. binaries − двойной) и при
− бинарным (от лат. binaries − двойной) и при  − тернарным (от лат. tertia – третья).
− тернарным (от лат. tertia – третья).


