
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторная форма записи системы.
Пусть
Задача Коши для системы (1). Найти частное решение
где точка В векторной форме начальные условия имеют вид
где Опр. Семейство вектор-функций 1. 2. Для Векторная форма общего решения -
Теорема существования и единственности решения задачи Коши для нормальных систем. Пусть функции Сведение ДУ n-го порядка к нормальной системе. Рассмотрим ДУ -го порядка
Введем обозначения:
Тогда уравнение (2.14.3) равносильно системе
Пример.
Сведение нормальной системы к одному уравнению n-го порядка. Рассмотрим случай
Сведем к ДУ 2-го порядка. Из 1-го уравнения
Если из 1-го уравнения системы можно выразить
Тогда Пример.
Продифференцируем 1-е уравнение:
Из 1-го уравнения:
Характеристическое уравнение полученного ЛОДУ с постоянными коэффициентами:
2.15.Автономные системы ДУ. Фазовое пространство и фазовые траектории. Первые интегралы систем ДУ. Симметричная форма записи систем ДУ и ее применение к нахождению первых интегралов.
Если Фазовая плоскость. Рассмотрим
Пусть вектор-функция
Кривая
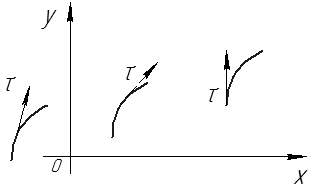
Касательный вектор к фазовой кривой в произвольной точке (см. рис. 41):
Рис. 41 Рассмотрим
Таким образом фазовые кривые системы
Пример.
ДУ фазовых кривых:
Рис. 42 Первые интегралы нормальных систем ДУ. Опр. Равенство
называется первым интегралом системы 1. Функция 2. Для
Первый интеграл позволяет понизить число уравнений в системе. Пусть в т.
Подставив
Чтобы полностью решить систему
Независимость первых интегралов означает, что ни один из них не может быть выражен через остальные. Система Симметричная форма записи нормальных систем ДУ:
Получив из симметричной формы системы интегрируемые комбинации (полные дифференциалы), можно найти 1-е интегралы. При нахождении интегрируемых комбинаций удобно использовать следующее свойство пропорций:
Пример 1.
Симмметричная форма системы:
По свойству пропорций получаем
Аналогично
Пример 2.
Для автономной системы найдем два независимых 1-х интеграла, не содержащих
Симметричная форма системы:
Чтобы найти второй 1-й интеграл запишем симметричную форму системы в виде
Таким образом, найденные первые интегралы задают фазовые кривые системы:
Пример 3.
Симметричная форма:
2.16.Нормальные системы ЛДУ, однородные и неоднородные. Матричная запись системы. Линейность пространства решений системы ЛОДУ. Вронскиан системы вектор-функций и его свойства. Теорема о размерности пространства решений системы ЛОДУ. Структура общего решения. Фундаментальная система решений.
– нормальная система ЛНДУ, здесь Если Матричная форма системы ЛДУ
где матрица
Соответствующая
Теорема. Множество всех частных решений системы ЛОДУ Док-во: пусть
т.е. Аналогично при
т.е.
|
||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.170 (0.037 с.) |
 . Тогда система (2.14.1) можно записать в виде
. Тогда система (2.14.1) можно записать в виде
 Опр. Вектор-функция
Опр. Вектор-функция 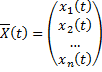 называется частным решением системы (2.14.1) на
называется частным решением системы (2.14.1) на 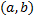 , если при ее подстановке в (2.14.1) все уравнения системы (2.14.1) обращаются в тождества на
, если при ее подстановке в (2.14.1) все уравнения системы (2.14.1) обращаются в тождества на 
 .
.

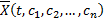 , зависящих от
, зависящих от 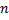 произвольных постоянных, называется общим решением системы (2.14.1), если
произвольных постоянных, называется общим решением системы (2.14.1), если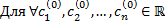 вектор-функция
вектор-функция  такие, что
такие, что 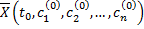 удовлетворяет начальному условию (2.14.2).
удовлетворяет начальному условию (2.14.2). .
. и их частные производные
и их частные производные  непрерывны в области
непрерывны в области  огда
огда 
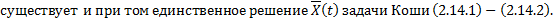

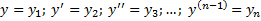 .
.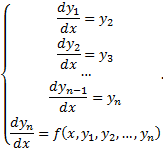
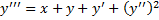 .
.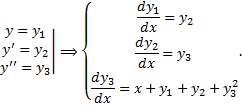

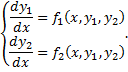
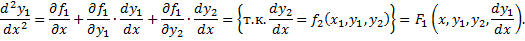
 , то для
, то для 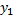 получим уравнение 2-го порядка:
получим уравнение 2-го порядка: (общее решение ДУ 2-го порядка).
(общее решение ДУ 2-го порядка).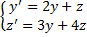 .
.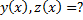
 .
.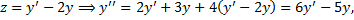
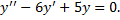
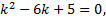
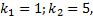
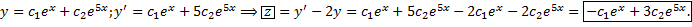

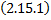 – нормальная система ОДУ.
– нормальная система ОДУ.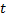 – независимая переменная,
– независимая переменная, – независимые функции,
– независимые функции,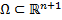 .
.

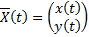 – частное решение автономной системы
– частное решение автономной системы  . Рассмотрим на плоскости
. Рассмотрим на плоскости  кривую
кривую  , заданную параметрическими уравнениями
, заданную параметрическими уравнениями
 на фазовой плоскости
на фазовой плоскости 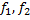 имеют непрерывные частные производные первого порядка в области
имеют непрерывные частные производные первого порядка в области 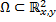 , то через каждую точку области
, то через каждую точку области 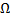 проходит ровно одна фазовая кривая.
проходит ровно одна фазовая кривая.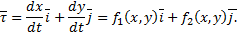
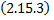 как функцию
как функцию 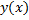 , заданную параметрически, тогда
, заданную параметрически, тогда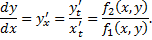
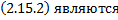 интегральными кривыми ДУ 1-го порядка
интегральными кривыми ДУ 1-го порядка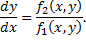
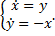
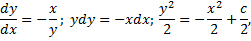
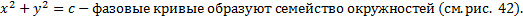



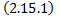 в области
в области 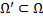 , если выполняется 2 условия:
, если выполняется 2 условия: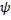 имеет непрерывные частные производные 1-го порядка в области
имеет непрерывные частные производные 1-го порядка в области 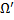 и для
и для 
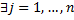 , что
, что 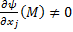 .
.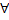 решения системы
решения системы 
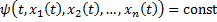 .
. 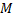
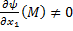 . Тогда по теореме о неявной функции из
. Тогда по теореме о неявной функции из 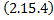 можно в некоторой окрестности т.
можно в некоторой окрестности т. 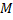 выразить
выразить 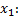
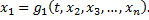
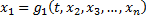 в уравнения системы
в уравнения системы 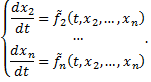

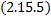 неявно задает решение системы.
неявно задает решение системы.
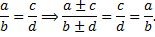


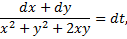


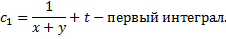

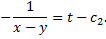
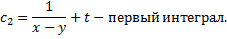

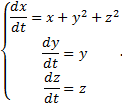



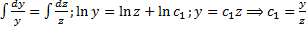 - (1-й интеграл).
- (1-й интеграл).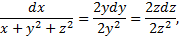
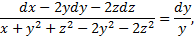
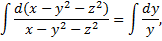
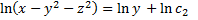 ,
,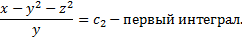
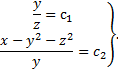

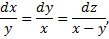
 ,
,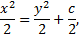
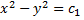 - 1-й интеграл.
- 1-й интеграл.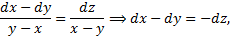
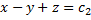 - 1-й интеграл.
- 1-й интеграл.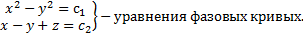

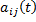 ,
, 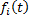 – функции, непрерывные на некотором интервале
– функции, непрерывные на некотором интервале 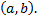
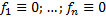 , то
, то 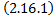 – система ЛОДУ.
– система ЛОДУ.
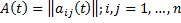
 .
.

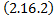 является линейным пространством относительно операций сложения вектор-функций и их умножения на число.
является линейным пространством относительно операций сложения вектор-функций и их умножения на число. – решения системы
– решения системы  . Имеем
. Имеем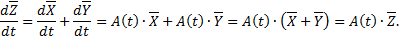
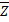 – решение
– решение 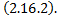
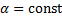 и вектор-функции
и вектор-функции  получаем
получаем
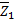 удовлетворяет системе
удовлетворяет системе 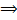 решения
решения 



