
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о структуре общего решения неоднородного лду n-го порядка. Теорема о наложении частных решений.
Теорема (о структуре общего решения неоднородного ЛДУ n-го порядка). Пусть Док-во: нужно доказать, что
Решение задачи Коши существует и определено на
Т.е.
Теорема (о наложении частных решений). Пусть Док-во:
2.11. ЛОДУ с постоянным коэффициентами. Характеристическое уравнение и построение общего решения по его корням (вывод для
Рассмотрим случай
Для произвольного
Тогда
Опр. Уравнение
Таким образом, при Построение ФСР ЛОДУ с постоянными коэффициентами по корням характеристического уравнения. Случай различных действительных корней. Пусть
образуют ФСР ЛОДУ. Док-во:
( При Тогда
Пример.
Характеристическое уравнение:
Случай кратных действительных корней. Пусть Корню
Док-во: (для n=2)
Пусть
Тогда по теореме Виета
Покажем, что
(
Тогда
Пример.
Характеристическое уравнение:
ФСР:
Случай комплексных корней кратности 1. Пусть
Док-во: Рассмотрим комплексную показательную функцию, которую введем по формуле Эйлера
Покажем, что
Тогда для функции
Т.к.
– решения ЛОДУ, они линейно независимы, т.к. Примеры. 1.
ФСР:
2.
ФСР:
4. случай кратных комплексных корней (возможен только при Пусть
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.171.20 (0.027 с.) |

 – линейный дифференциальный оператор с переменными коэффициентами
– линейный дифференциальный оператор с переменными коэффициентами 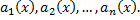
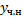 – частное решение ЛНДУ
– частное решение ЛНДУ 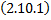 . Тогда
. Тогда 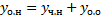
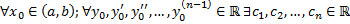 такие, что функция
такие, что функция 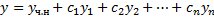 – решение ЛНДУ, удовлетворяющее начальным условиям
– решение ЛНДУ, удовлетворяющее начальным условиям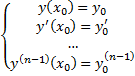 .
.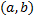 в силу теоремы существования. Рассмотрим разность
в силу теоремы существования. Рассмотрим разность 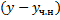 :
: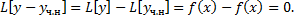
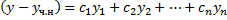 – решение ЛОДУ;
– решение ЛОДУ; 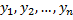 – ФСР ЛОДУ;
– ФСР ЛОДУ; 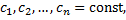
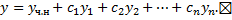
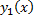 – частное решение ЛНДУ;
– частное решение ЛНДУ; 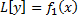 ;
; 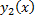 – частное решение ЛНДУ;
– частное решение ЛНДУ; 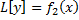 . Тогда
. Тогда 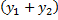 – частное решение ЛНДУ
– частное решение ЛНДУ 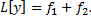
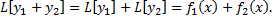

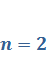 ).
).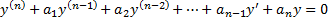 ,
,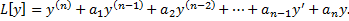
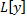 – линейный дифференциальный оператор с постоянными коэффициентами:
– линейный дифференциальный оператор с постоянными коэффициентами: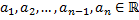 .
.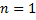 :
: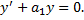
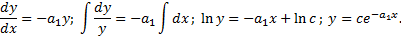
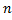 найдем частное решение вида
найдем частное решение вида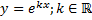 .
.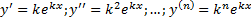 .
.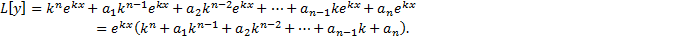
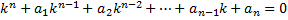 называется характеристическим уравнением ЛОДУ с постоянными коэффициентами.
называется характеристическим уравнением ЛОДУ с постоянными коэффициентами.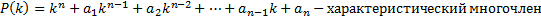
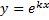 имеем
имеем 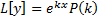 и функция
и функция 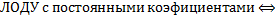
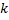 является корнем его характеристического уравнения.
является корнем его характеристического уравнения.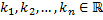 - различные корни характеристического уравнения. Тогда функции
- различные корни характеристического уравнения. Тогда функции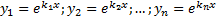
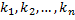 - корни характеристического уравнения. Покажем, что
- корни характеристического уравнения. Покажем, что 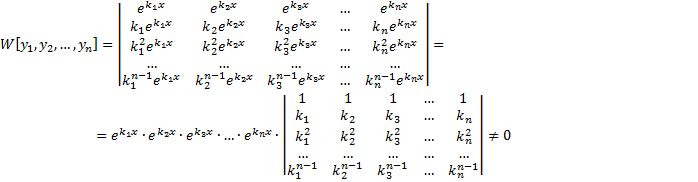
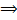

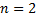 :
: 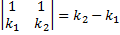 ).
).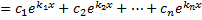 .
.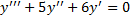 .
.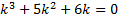 ,
,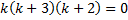 ,
,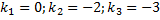 ,
,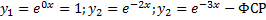 ,
,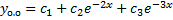 .
.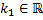 - корень кратности
- корень кратности 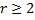 , т.е.
, т.е. 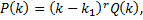
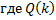 – многочлен, причем
– многочлен, причем 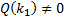 .
.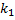 кратности
кратности 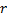 линейно независимых решений:
линейно независимых решений: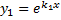
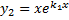
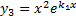

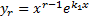 .
.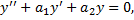
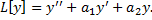
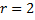 характеристического уравнения
характеристического уравнения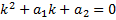 .
.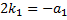 .
.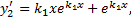
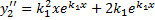 .
.
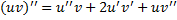 ).
).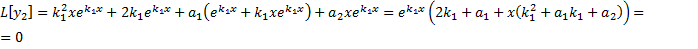 .
.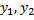 – решения, линейно независимые, т.к.
– решения, линейно независимые, т.к. 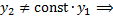
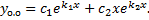
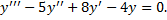
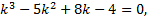
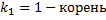 ,
,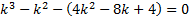 ,
,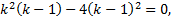
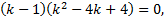
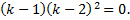
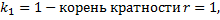
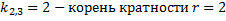 .
.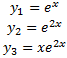 .
.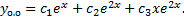
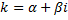 – корень характеристического уравнения кратности 1
– корень характеристического уравнения кратности 1 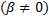 . Тогда
. Тогда 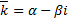 – также корень кратности 1. Паре корней
– также корень кратности 1. Паре корней 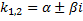 соответствуют 2 линейно независимых решения:
соответствуют 2 линейно независимых решения: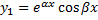
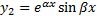 .
.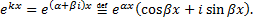
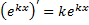 при
при 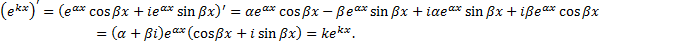
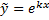
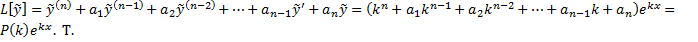 е.
е. 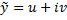 – решение, то
– решение, то 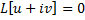 , т.е.
, т.е. 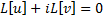 , т.е. функции
, т.е. функции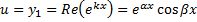 ,
,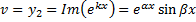
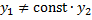 .
.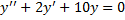 .
.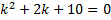 ,
,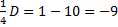 ,
,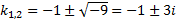 ,
,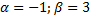 .
.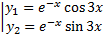 ,
,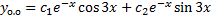 .
.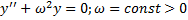 .
.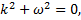
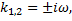
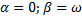 ,
,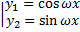 .
.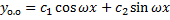 .
.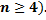
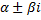 – корни кратности
– корни кратности 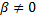 . Им соответствуют
. Им соответствуют 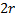 линейно независимых решений:
линейно независимых решений: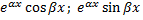
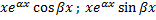
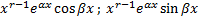 .
.


