Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация ДУ 1-го порядка. Поле направлений. Геометрическое решение ДУ 1-го порядка с помощью изоклин.
Пусть для ДУ Угловой коэффициент касательной к интегральной кривой в точке
Рис. 32 Опр. Изоклиной ДУ (2.1.2) называется кривая, во всех точках которой угловой коэффициент касательной к интегральной кривой, проходящей через заданную точку, одинаковый и равен заданному Уравнение изоклины:
Рис. 33 Пример.
Рис. 34 Уравнение изоклин:
Прямая
При При Отсюда на прямой
Простейшие типы ДУ 1-го порядка (с разделяющимися переменными, однородные, линейные, Бернулли) и их решение.
1. ДУ с разделяющимися переменными
или
Запишем ДУ в виде
Проинтегрируем:
Замечание. Если уравнение Пример.
2. Однородные ДУ
Замена
Тогда, подставляя в ДУ получим
Пример.
Замена:
3. Линейные ДУ 1-го порядка.
I. ЛОДУ 1-го порядка.
(р II. ЛНДУ 1-го порядка.
a. Решим соответствующее ЛОДУ: b. Решение ЛНДУ ищем методом вариации постоянной, т.е. в виде
Тогда Подставим в ЛНДУ:
Находим Пример.
a. Соответствующее ЛОДУ: b. Ищем решение ЛНДУ в виде Подставляем в ЛНДУ:
Проинтегрировав, получим
Подставим в (2.3.1):
Замечание. ДУ
сводится к ЛНДУ относительно обратной функции
Решаем методом вариации произвольной постоянной:
4. Уравнения Бернулли
Ищем решения в виде
Найдем функцию
Используя (2.3.2), получим
– ДУ с разделяющимися переменными. Найдем Пример.
Найдем
Подставим
Тогда
Замечание. ДУ
сводится к ДУ Бернулли относительно функции
Решение ищем в виде
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.212.211 (0.015 с.) |

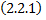 выполняется условие существования и единственности, т.е. через любую точку
выполняется условие существования и единственности, т.е. через любую точку 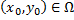 проходит ровно одна интегральная кривая - график частного решения
проходит ровно одна интегральная кривая - график частного решения 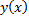 .
.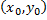 равен
равен 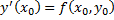 . Таким образом, в каждой точке области
. Таким образом, в каждой точке области 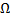 ДУ (2.1.2) задает направление касательной к интегральной кривой, проходящей через эту точку
ДУ (2.1.2) задает направление касательной к интегральной кривой, проходящей через эту точку 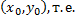 В
В 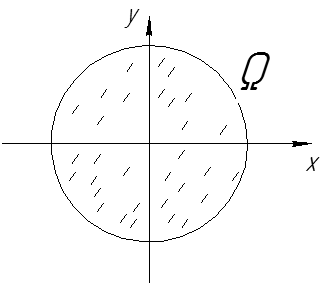
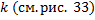 .
.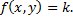
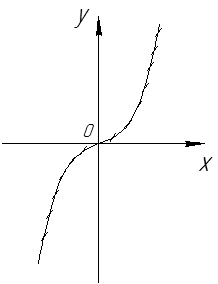
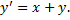
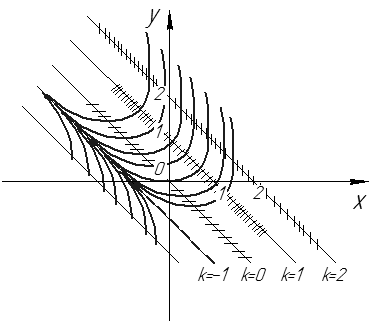
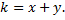
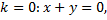
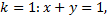
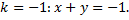
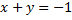 является изоклиной
является изоклиной 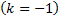 и является интегральной кривой, т.к.
и является интегральной кривой, т.к. 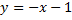 – частное решение ДУ, т.е. является асимптотой для интегральных кривых (другие интегральные кривые приближаются к этой прямой, но не пересекают ее, т.к. через одну точку проходит только одна интегральная кривая.)
– частное решение ДУ, т.е. является асимптотой для интегральных кривых (другие интегральные кривые приближаются к этой прямой, но не пересекают ее, т.к. через одну точку проходит только одна интегральная кривая.)
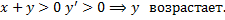
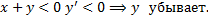
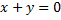 находятся точки локального минимума решений ДУ.
находятся точки локального минимума решений ДУ.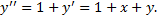
 .
.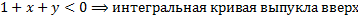 (см. рис. 34).
(см. рис. 34).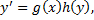
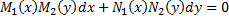 .
.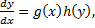
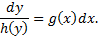
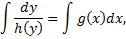
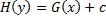 – общий интеграл,
– общий интеграл, 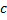 – произвольная постоянная.
– произвольная постоянная.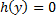 имеет корни
имеет корни  , то функции
, то функции 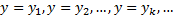 являются частными решениями ДУ.
являются частными решениями ДУ.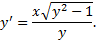
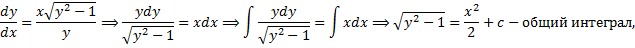
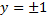 – также решение ДУ.
– также решение ДУ.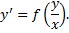
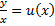 , тогда
, тогда 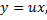


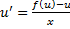 – ДУ с разделяющимися переменными, находим
– ДУ с разделяющимися переменными, находим 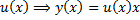 .
.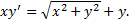
 (x>0).
(x>0).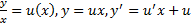 . Подставим в ДУ:
. Подставим в ДУ: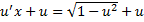 ,
,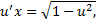
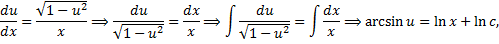
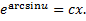
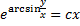 – общий интеграл.
– общий интеграл.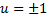 – решение, т.е.
– решение, т.е. 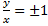 , т.е.
, т.е. 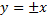 .
. – линейное однородное ДУ (ЛОДУ) 1-го порядка.
– линейное однородное ДУ (ЛОДУ) 1-го порядка.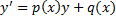 – линейное неоднородное ДУ (ЛНДУ) 1-го порядка.
– линейное неоднородное ДУ (ЛНДУ) 1-го порядка.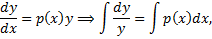
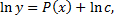
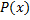 – первообразная
– первообразная 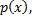
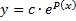
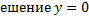 получаем при
получаем при 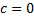 ).
).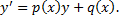
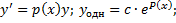
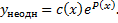
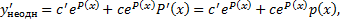
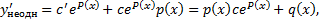
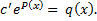
 ; интегрируем, находим
; интегрируем, находим  .
.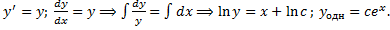

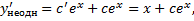
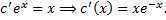
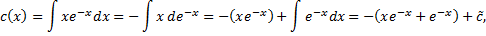

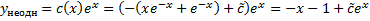 =
= 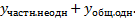
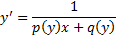


 .
.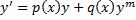 ,
,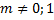 .
.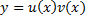 . Подставим в ДУ:
. Подставим в ДУ: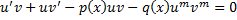 ,
,
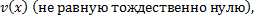 такую, что
такую, что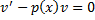 – ДУ с разделяющимися переменными (ЛОДУ).
– ДУ с разделяющимися переменными (ЛОДУ).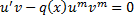
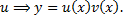
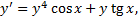
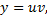
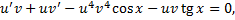
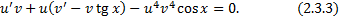
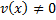 из ДУ
из ДУ 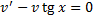 .
.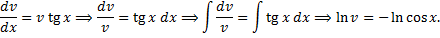
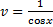 в (2.3.3):
в (2.3.3):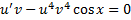 ,
,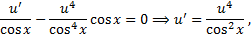

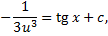
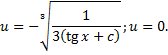
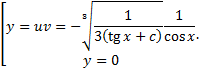
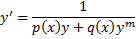
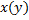 :
: