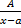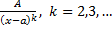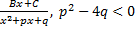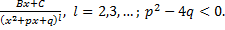Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подведение под знак дифференциала.
Пусть Рассмотрим сложную функцию
Примеры. 1. 2. 3.
Замена переменной. Поменяем в (1.2.1) местами где Пусть
Т.е.
Пример.
Интегрирование по частям Пусть функции Док-во:
Примеры. 1. 2. 3. т.е.
Интегрирование выражений, содержащих квадратный трехчлен I. Выделим полный квадрат, получим табличный интеграл (10-13) Примеры. 1. 2. II. Выделим в числителе производную квадратного трехчлена
где Аналогично
где Примеры. 1. 2. Интегрирование тригонометрических функций. 1.
Пример.
2.
Пример.
3.
Пример.
4.
Пример.
5.
Пример.
Где 6. Преобразование произведения тригонометрических функций в сумму. 7. Подстановка Пример. 8. Подстановка
Пример.
Интегрирование иррациональных функций. I. Замена Пример.
II. Замена Пример.
III. Выделив полный квадрат, получим интеграл одного из видов: a) Замена Пример.
b) Замена Пример.
c) Замена Пример.
Примеры интегралов, не выражающихся через элементарные функции:
Интегрирование рациональных дробей. Разложение правильной рациональной дроби в сумму простейших. Интегрирование простейших дробей. Интегрирование неправильных рациональных дробей.
Рациональная дробь
где
Опр. Рациональная дробь Опр. Рациональная дробь Пусть
Пример.
Разложение многочлена на множители. Пусть
Тогда где
Пример.
Простейшие рациональные дроби. Опр. Простейшими называют рациональные дроби одного из следующих видов: 1. 2. 3. 4.
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 63; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.87.152 (0.027 с.) |
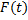 – первообразная функции
– первообразная функции 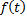 на
на 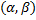 , т.е.
, т.е. 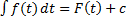 . Рассмотрим замену
. Рассмотрим замену 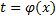 , где
, где  – дифференцируемая на
– дифференцируемая на 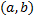 функция,
функция,  .
.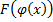 ,
, 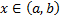 .
. , т.е.
, т.е. 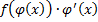 , т.е.
, т.е.  , или
, или 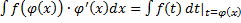 , или
, или 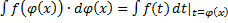 ,
,
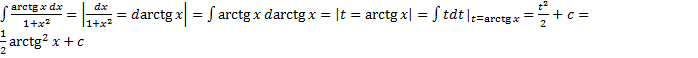
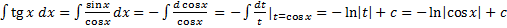
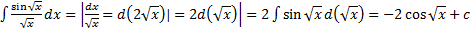 .
.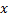 и
и 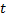 :
:  ,
,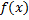 определена на
определена на 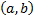 ,
, 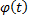 дифференцируема на
дифференцируема на 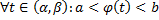 .
.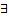 обратная функция
обратная функция 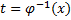 . Заменим
. Заменим 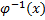 :
: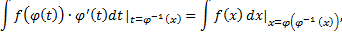
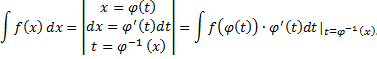
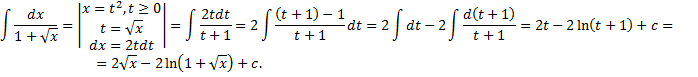
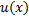 и
и  дифференцируемы на
дифференцируемы на  , т.е.
, т.е. 
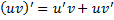 , т.е.
, т.е. 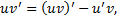
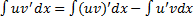 , т.е.
, т.е. 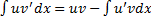 ,
,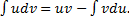

 .
.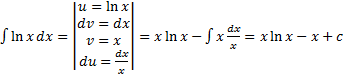 .
.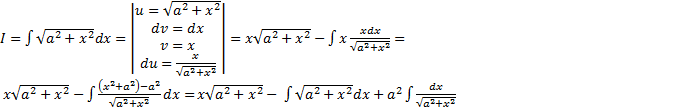 ,
, , т.е.
, т.е.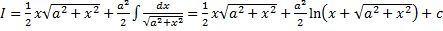 .
. ,
, 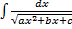 .
.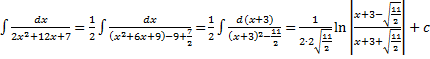 .
.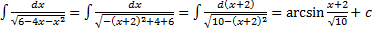 .
.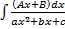 ,
, 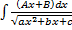 .
.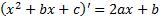 , т.е. представим числитель в виде
, т.е. представим числитель в виде 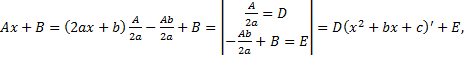
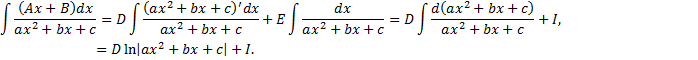
 – находится с помощью выделения полного квадрата.
– находится с помощью выделения полного квадрата.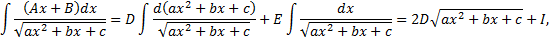
 .
.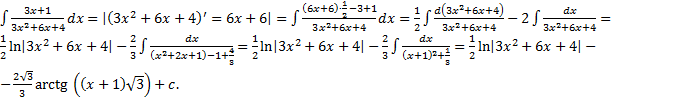
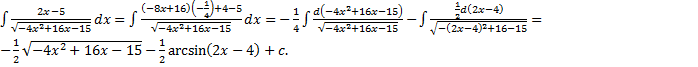
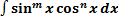 , где
, где 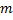 или
или 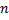 – нечетное натуральное число (например,
– нечетное натуральное число (например,  )
)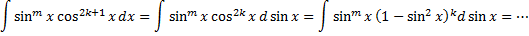
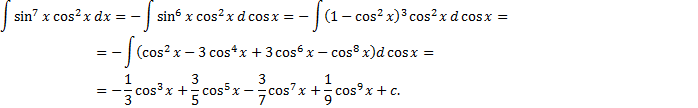
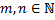 – четные. Используем формулы понижения степени
– четные. Используем формулы понижения степени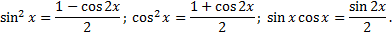
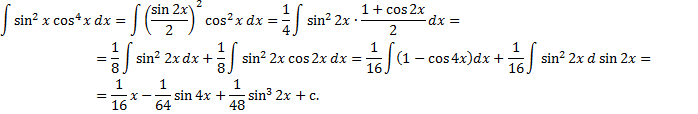
 где
где 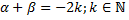 (т.е.
(т.е. 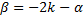 ). Используем формулы
). Используем формулы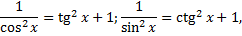
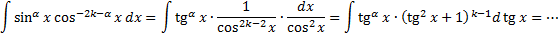
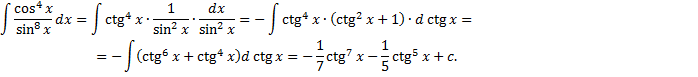
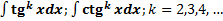 . Понижение показателя с использованием формул
. Понижение показателя с использованием формул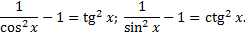

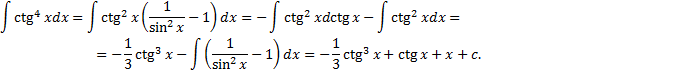
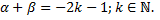 Понижение степени с использованием формул:
Понижение степени с использованием формул: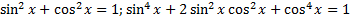 и т.д.
и т.д.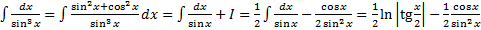 +c,
+c,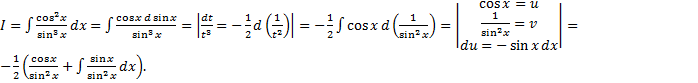

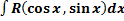 , где
, где 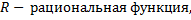
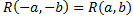 .
.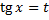 .
.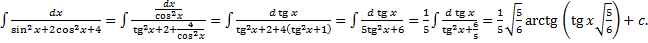
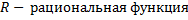 .
.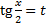 ,
,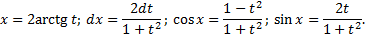
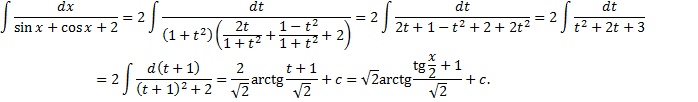
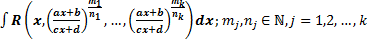 .
.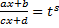 ,
, 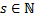 –общий знаменатель
–общий знаменатель  (Н.О.К.
(Н.О.К.  ).
).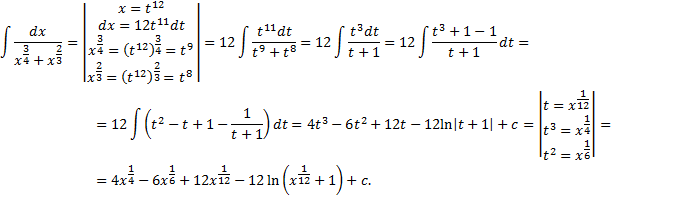

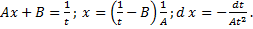
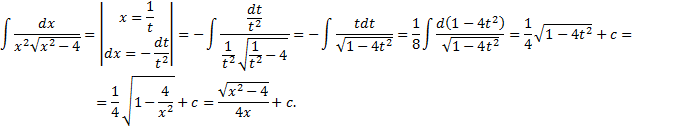
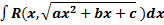 .
.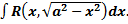
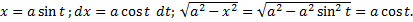
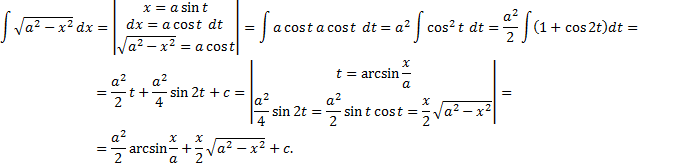
 .
. .
.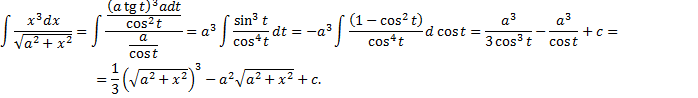
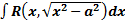 .
.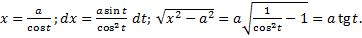
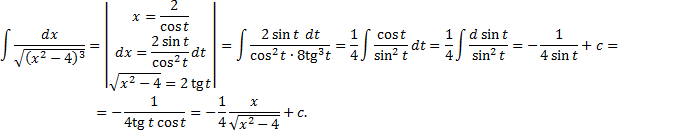
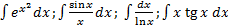 («неберущиеся» интегралы).
(«неберущиеся» интегралы).
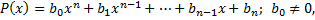
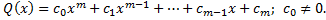
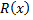 называется правильной, если
называется правильной, если 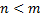 .
.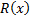 называется неправильной, если
называется неправильной, если  .
. – неправильная дробь. Разделим с остатком
– неправильная дробь. Разделим с остатком 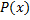 на
на 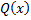 , т.е. представим
, т.е. представим 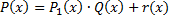 , где
, где 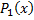 – многочлен степени
– многочлен степени 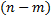 , степень многочлена
, степень многочлена 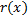 меньше
меньше 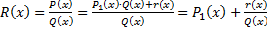 , где
, где  – правильная рациональная дробь.
– правильная рациональная дробь.

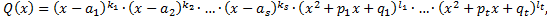 (1.3.1)
(1.3.1)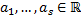 – корни многочлена
– корни многочлена 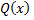 кратности
кратности 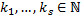 соответственно,
соответственно, 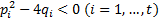 .
. .
.