
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
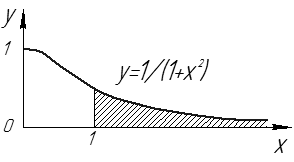
Вычисление несобственного интеграла 1-го рода.
Пусть
Таким образом,
Примеры.
Рис. 10
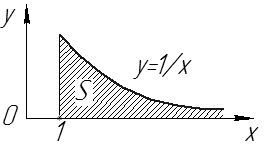
Рис. 11 3.
Рис. 12 4.
Исследование несобственных интегралов 1-го рода на сходимость.
 Признаки сходимости: Признаки сходимости:
1. Признак сравнения. Пусть a. Если b. Если 2. Предельный признак сравнения: пусть для Тогда 3. Если сходится В качестве «образцов» интегралов для сравнения обычно используются интегралы Примеры. 1.
При
3. Т.к. при
Несобственные интегралы 2-го рода
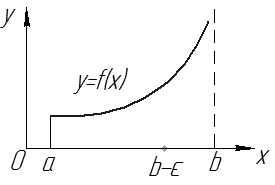 Пусть Пусть 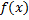 непрерывна на непрерывна на 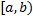 , но не ограничена в левой окрестности точки , но не ограничена в левой окрестности точки 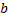 . Определенный интеграл . Определенный интеграл 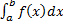 не существует, т.к. не существует, т.к. 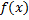 – неограниченная. Рассмотрим – неограниченная. Рассмотрим 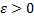 . Т.к. . Т.к. 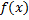 непрерывна на непрерывна на 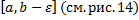 , то , то 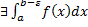 – определенный интеграл. – определенный интеграл.
Опр. Несобственным интегралом 2 рода по
Если существует конечный предел (1.8.2), то несобственный интеграл 2-го рода называется сходящимся, в противном случае – расходящимся. Геометрический смысл: при
Рис. 15
Рис. 16 Свойство линейности. Если
Вычисление несобственного интеграла 2-го рода. Случай функции с особой точкой
Таким образом, Примеры.
Рассмотрим интегралы
Рассмотрим случай интеграла с особой точкой в левом конце отрезка:
Случай
Аналогично рассматривается интеграл с особой точкой в правом конце отрезка. Таким образом
Исследование несобственных интегралов 2-го рода на сходимость. Признаки сходимости: 1. Признак сравнения: пусть a. Если b. Если 2. Предельный признак сравнения. Пусть для Тогда 3. Если сходится Примеры. 1.
При
2.
При
Замечание: если
(для первого и второго интегралов в правой части особой точкой является
Пример.
Примеры несобственных интегралов с несколькими особыми точками 1. Исходный интеграл сходится, если сходятся оба интеграла в правой части: a.
b.
(несобственный интеграл 2-го рода a. b. Значит,
a. При b. При Таким образом исходный интеграл расходится.
|
|||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.196.182 (0.028 с.) |
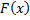 – первообразная для
– первообразная для 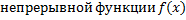 на
на 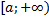 , тогда
, тогда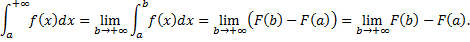
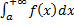 сходится
сходится 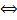
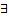 конечный предел первообразной
конечный предел первообразной 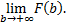
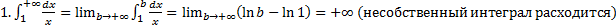 ,
, 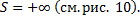

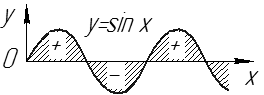
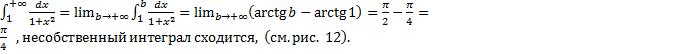
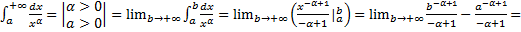
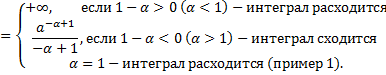
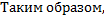
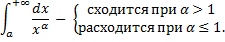
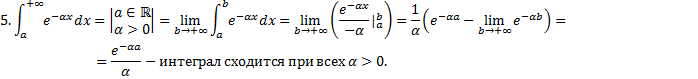
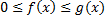
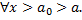
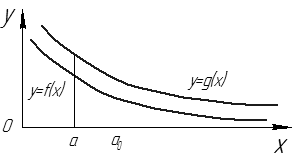
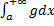 сходится, то
сходится, то  также сходится (см. рис. 13).
также сходится (см. рис. 13).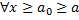
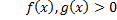 и
и 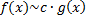 при
при 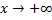 , т.е.
, т.е. 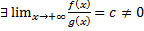 .
.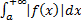 , то сходится и
, то сходится и  (a>0).
(a>0).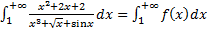 .
.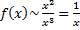 при
при 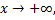
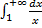 расходится
расходится 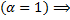 исходный интеграл расходится по предельному признаку.
исходный интеграл расходится по предельному признаку.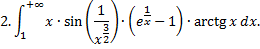
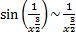 ;
; 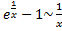 ;
; 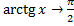 ,
,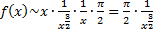 ;
; 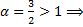 интеграл сходится по предельному признаку.
интеграл сходится по предельному признаку.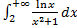
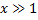
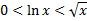 (логарифм растет медленней степенной функции), то
(логарифм растет медленней степенной функции), то 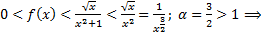 исходный интеграл сходится по признаку сравнения.
исходный интеграл сходится по признаку сравнения.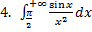 .
.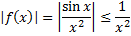
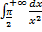 – сходится
– сходится 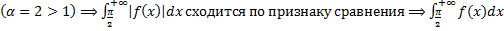 сходится по признаку 3.
сходится по признаку 3.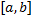 от функции
от функции 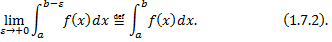
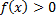 – площадь фигуры, ограниченной линиями
– площадь фигуры, ограниченной линиями 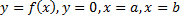 (см. рис. 15).
(см. рис. 15).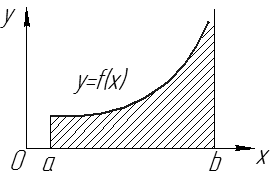
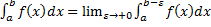 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 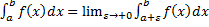 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 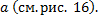
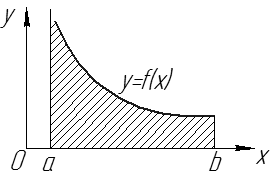
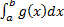 сходятся, то сходятся интегралы
сходятся, то сходятся интегралы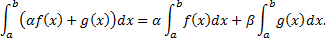
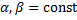 .
.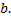
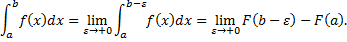
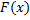 – первообразная для
– первообразная для 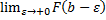 .
.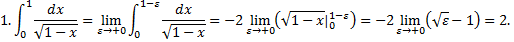

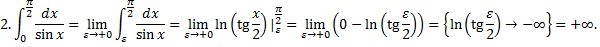
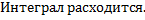
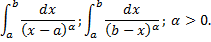
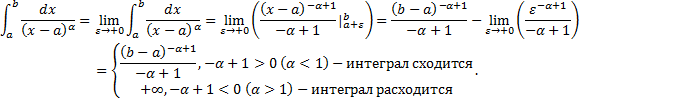
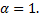
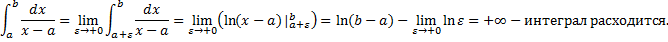
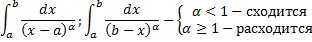
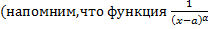 имеет при
имеет при 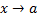 порядок роста
порядок роста 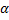 относительно
относительно 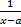 ).
).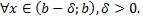
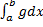 сходится, то
сходится, то 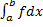 также сходится.
также сходится.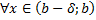
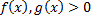 и
и 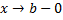 , т.е.
, т.е. 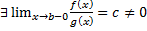 .
.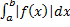 , то сходится и
, то сходится и 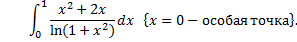
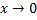
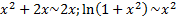 ,
,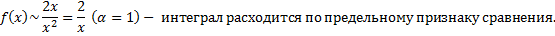
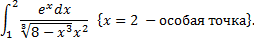
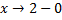
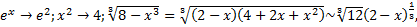
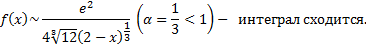
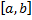 кроме точки
кроме точки 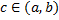 и
и 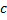 , тогда
, тогда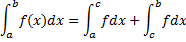
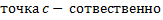 правый или левый конец отрезка).
правый или левый конец отрезка).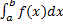 сходится
сходится 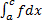 и
и 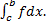
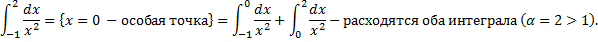
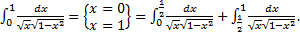
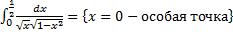 .
.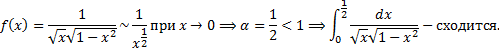
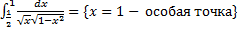 .
.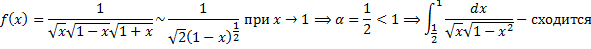
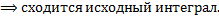
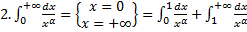 .
.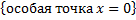 + несобственный интеграл 1-го рода
+ несобственный интеграл 1-го рода 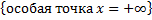 ).
).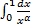 – сходится при
– сходится при 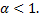
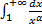 – сходится при
– сходится при 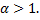
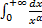 расходится для любого
расходится для любого 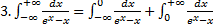 .
.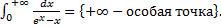
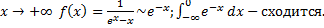
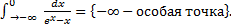
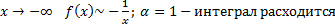 .
.


