
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные ДУ (ЛОДУ) n-го порядка.
Теорема. Множество частных решений ЛОДУ n-го порядка Док-во. Нужно доказать, что операции сложения частных решений и умножения частных решений на число не выводит из множества частных решений, т.е. сумма частных решений Пусть Итак, решения ЛОДУ n-го порядка
Линейная зависимость функций. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно зависимых функций и о вронскиане системы линейно независимых частных решений ЛОДУ.
Опр. Функции
Опр. Если выполнение равенства ( Критерий линейной зависимости: Функции Пример.
Т.к. Пусть функции Опр. Определителем Вронского (вронскианом) системы функций
Теорема о вронскиане системы линейно зависимых функций Пусть функции Док-во: по определению линейной зависимости функций
Зафиксируем (2.7.2) – СЛАУ (однородных) относительно Замечание. Обратное неверно, т.е. если Пример.
Т.е. Теорема о вронскиане системы линейно независимых частных решений ЛОДУ Пусть Док-во: (от противного) Пусть
Ее определитель
Рассмотрим частное решение ЛОДУ
Оно удовлетворяет в т.
Рассмотрим частное решение ЛОДУ
Оно удовлетворяет в т.
Таким образом, частные решения ЛОДУ Т.е. Замечание. Пусть
Не может иметь вид (см. рис. 39, 40):
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.220.21 (0.008 с.) |
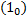 является линейным пространством относительно операций сложения функций и умножения на число.
является линейным пространством относительно операций сложения функций и умножения на число.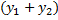 – также решение, произведение частного решения на число
– также решение, произведение частного решения на число 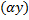 – также решение,
– также решение, 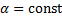 .
.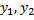 – решения, тогда
– решения, тогда 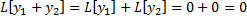 , т.е.
, т.е.  , т.е.
, т.е.  .
. 
 называются линейно зависимыми на
называются линейно зависимыми на 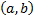 , если
, если 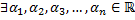 , не все равные
, не все равные  , такие, что
, такие, что 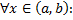

 ) на всем интервале
) на всем интервале 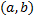 возможно только при
возможно только при  , то функции
, то функции 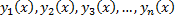 называются линейно независимыми на
называются линейно независимыми на 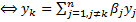 для некоторого k=1,….n (т.е. хотя бы одна из функций линейно выражается через остальные).
для некоторого k=1,….n (т.е. хотя бы одна из функций линейно выражается через остальные).

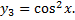
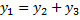 , то функции линейно зависимы на
, то функции линейно зависимы на 
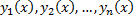
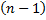 раз дифференцируемы на
раз дифференцируемы на 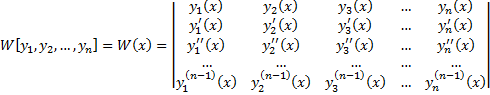 .
. :
: 
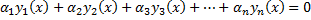 . Последовательно продифференцируем это равенство:
. Последовательно продифференцируем это равенство: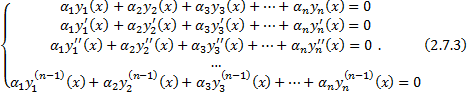
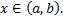
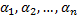 , которая имеет ненулевое решение, т.е. определитель системы равен
, которая имеет ненулевое решение, т.е. определитель системы равен 
 , то функции могут быть линейно независимы.
, то функции могут быть линейно независимы. ,
,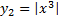 .
.
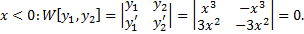
 на
на 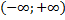 , но
, но 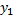 и
и  линейно независимы, т.к.
линейно независимы, т.к. 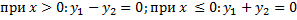 . Не существует
. Не существует 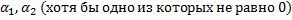 , таких, что
, таких, что 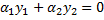 для всех
для всех 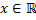 .
.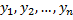 – линейно независимые на
– линейно независимые на 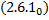 . Тогда
. Тогда 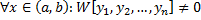
 . Рассмотрим СЛАУ относительно
. Рассмотрим СЛАУ относительно 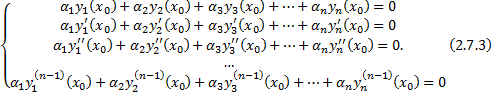
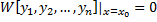 , следовательно, система имеет ненулевое решение, т.е.
, следовательно, система имеет ненулевое решение, т.е. 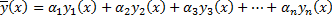 .
. начальным условиям (в силу (2.7.3)):
начальным условиям (в силу (2.7.3)):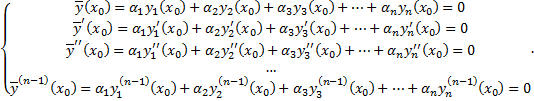
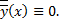
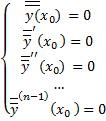 .
.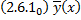 и
и  удовлетворяют одним и тем же начальным условиям задачи Коши. По теореме о единственности решения задачи Коши
удовлетворяют одним и тем же начальным условиям задачи Коши. По теореме о единственности решения задачи Коши 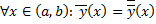 , т.е.
, т.е. 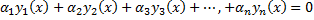 , т.е.
, т.е. 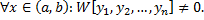
 может иметь вид (см. рис. 37, 38):
может иметь вид (см. рис. 37, 38):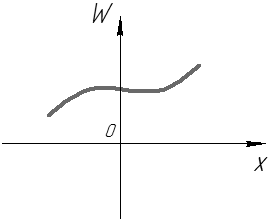 Рис. 37
Рис. 37
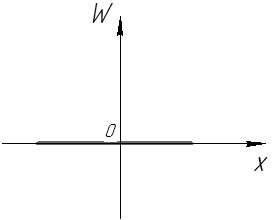 Рис. 38
Рис. 38



