
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сведение ДУ Бернулли к лнду.
Разделим на
Пусть
Подставим в ДУ:
Пример.
(ДУ Бернулли при Разделим на
Замена
Подставим, получим
Решая методом вариации постоянной, получим
и
2.4. ДУ n-го порядка. Частные и общее решения. Задача Коши, ее геометрическая интерпретация при n=2. Теорема существования и единственности решения задачи Коши. Краевая задача.
ДУ n-го порядка, разрешенное относительно старшей производной:
Опр. Функция Задача Коши для ДУ n-го порядка Найти частное решение ДУ (2.4.1), удовлетворяющее начальным условиям:
где точка При
геометрический смысл: найти интегральную кривую, проходящую через точку Теорема существования и единственности решения задачи Коши для ДУ n-го порядка Пусть функция Рассмотрим следующий вопрос. Пусть для ДУ n-го порядка выполняется условие существования и единственности. При каких
Опр. Общим решением ДУ n-го порядка (2.4.1) называется семейство функций 1. Для 2. Для Краевая задача для ДУ 2-го порядка: найти частное решение на отрезке [
удовлетворяющее краевым условиям
Опр. Равенство
Понижение порядка некоторых типов ДУ высших порядков.
1. (ДУ не содержит Замена Получаем для
Находим Пример.
Замена Получаем для
Замечание. ДУ 2. (ДУ не содержит явно
Замена
Пример.
Замена
Линейные ДУ (ЛДУ) n-го порядка: однородные (ЛОДУ) и неоднородные (ЛНДУ). Теорема существования и единственности решения. Линейный дифференциальный оператор. Свойства линейного дифференциального оператора и линейность пространства решений ЛОДУ.
ЛДУ n-го порядка (неоднородное):
Коэффициенты
(2.6.1)– ЛНДУ
Задача Коши для ДУ: найти частные решения, удовлетворяющие начальным условиям:
где Теорема существования и единственности решения задачи Коши для ЛДУ Пусть Рассмотрим левую часть ЛДУ (2.6.1) и (2.6.10) – дифференциальный оператор
Покажем, что
Таким образом, Операторная форма ЛДУ: ЛНДУ:
ЛОДУ:
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.206.243 (0.017 с.) |
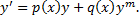
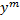 (при
(при 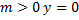 – решение):
– решение):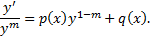
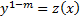 , тогда
, тогда 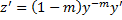 ,
,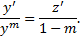
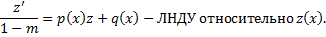
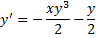
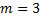 ;
; 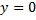 – решение).
– решение).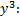
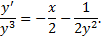
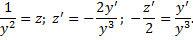
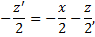
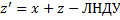 .
.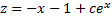 , т.е.
, т.е.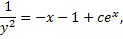
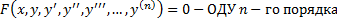 ,
,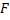 – функция от
– функция от 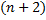 переменных.
переменных.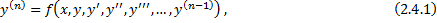
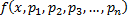 определена в области
определена в области 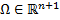 .
.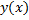 называется частным решением ДУ (2.4.1)на интервале
называется частным решением ДУ (2.4.1)на интервале 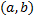 , если при ее подстановке в (2.4.1) получается тождество на
, если при ее подстановке в (2.4.1) получается тождество на 
 .
.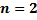 задача Коши имеет вид
задача Коши имеет вид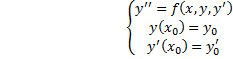 ,
,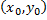 плоскости
плоскости 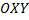 и имеющую заданный угловой коэффициент касательной
и имеющую заданный угловой коэффициент касательной 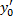 в т.
в т. 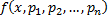 и ее частные производные
и ее частные производные 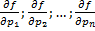 непрерывны в области
непрерывны в области 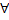 точки
точки 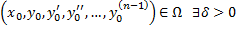 , что на интервале
, что на интервале 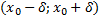 существует и при том единственное решение задачи Коши.
существует и при том единственное решение задачи Коши. возможно расположение интегральных кривых (см. рис. 35, 36)?
возможно расположение интегральных кривых (см. рис. 35, 36)?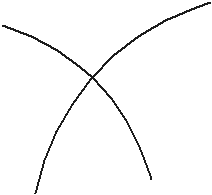 Рис. 35
Рис. 35
 Рис. 36
Рис. 36
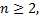
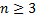 .)
.)
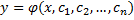 , зависящее от
, зависящее от  такое, что
такое, что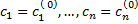 функция
функция 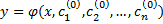 является частным решением ДУ (3).
является частным решением ДУ (3).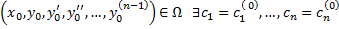 такие, что частное решение
такие, что частное решение 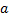 ,
, 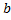 ] ДУ
] ДУ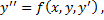
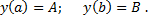
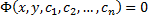 , неявно задающее общее решение ДУ n-го порядка называется общим интегралом ДУ n-го порядка.
, неявно задающее общее решение ДУ n-го порядка называется общим интегралом ДУ n-го порядка.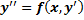
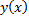 )
)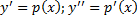
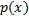 ДУ 1-го порядка:
ДУ 1-го порядка: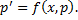
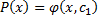 . Тогда
. Тогда 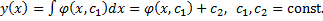
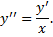
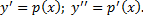
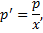
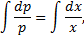
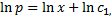
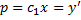
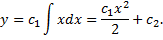
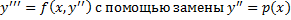 , сводится к ДУ
, сводится к ДУ 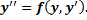
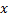 )
)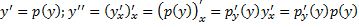 . Подставим в ДУ:
. Подставим в ДУ: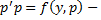 ДУ 1-го порядка относительно
ДУ 1-го порядка относительно 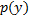 . Решая его, получаем общее решение
. Решая его, получаем общее решение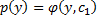 .
.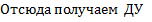 с разделяющимися переменными
с разделяющимися переменными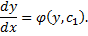
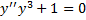 .
.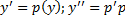 . Подставим в ДУ:
. Подставим в ДУ: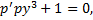
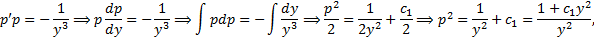

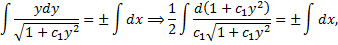
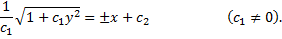
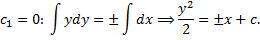
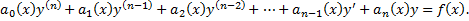
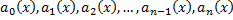 и правая часть
и правая часть 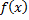 – функции, непрерывные на
– функции, непрерывные на 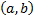 или на
или на 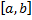 . Для
. Для  . Разделим на
. Разделим на 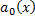 . Получим ДУ вида
. Получим ДУ вида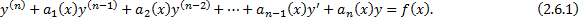
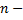 го порядка. Соответствующее ЛОДУ:
го порядка. Соответствующее ЛОДУ: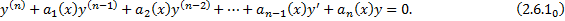

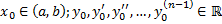 .
.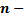 го порядка
го порядка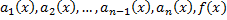 непрерывны на
непрерывны на 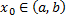 и
и 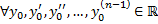
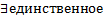 решение задачи Коши (2.6.1),(2.6.2), причем оно определено на всем интервале
решение задачи Коши (2.6.1),(2.6.2), причем оно определено на всем интервале 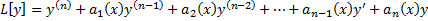 .
.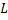 является линейным оператором, т.е.
является линейным оператором, т.е. 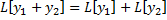 и
и 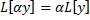 , где
, где 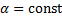 .
.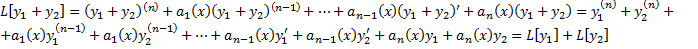 ,
,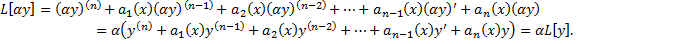
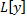 – линейный дифференциальный оператор.
– линейный дифференциальный оператор.




