
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисления с простыми и десятичными дробями
При решении практических задач часто приходится иметь дело одновременно и с простыми, и с десятичными дробями. Приходится, например, выполнять действия, вроде следующих: 0,3 + Напомним, как обратить десятичную дробь в простую: превратим, например, 0,36 в простую дробь. Прочитываем эту дробь; имеем тридцать шесть сотых; значит, знаменателем будет 100, а числителем 36. Записываем 0,36 = Итак, чтобы превратить десятичную дробь в простую, прочитываем десятичную дробь и записываем её в форме простой дроби так, как читаем; затем, что можно - сокращаем. Если нужно превратить простую дробь с десятичную, то делим числитель на знаменатель по обычным правилам. Чаще всего деление продолжается при этом без конца (получается периодическая дробь) и приходится довольствоваться приближённым результатом.
Примеры: 1) Превратить
Получим 0, 15625.
2) Превратить 3/7 в десятичную дробь. Делим 3 на 7:
Деление никогда не закончится. Получится периодическая дробь 0,428571428571428571..., которую записывают часто так: 0,(428571), т.е. пишут только первый период, но заключают его в скобки.
Примеры: превратить в простые дроби: 0,72; 0,0128; 0,625; 0,17; 0,3; 0,2. Превратить в десятичные дроби:
Если нужно сложить или вычесть дроби, среди которых есть и простые с небольшими знаменателями, и десятичные, то превращаем все дроби в простые и выполняем действие по обычным правилам.
Примеры: 1) 0,42 + = = = =
Общий знаменатель 750. Дополнительные множители 15, 250, 150 и 6. 2) 3) 0,096 - При умножении и делении нет надобности сводить все данные дроби либо только к простым, либо только к десятичным. Действуем с десятичными дробями по тем же правилам, как и с целыми числами. Умножим, например, 4,5 на 4,5∗ Нет никакой надобности превращать 4,5 в простую дробь или в десятичную. Разделим, далее, 0,133 на
Всё выполняется просто и гладко. Заметим, что помнить все правила деления дроби на целое число, целого числа на дробь и т.д. не нужно. Важно твёрдо помнить правило деления дроби на дробь: числитель первой дроби умножается на знаменатель второй, это будет числитель частного; знаменатель первой дроби умножается на числитель второй, это будет знаменатель частного. Ещё лучше просто представлять себе схему (деление дробей «крест-накрест»).
Если делимое (или делитель) будет целым числом (или десятичной дробью), то подписываем под ним в качестве энаменателя единицу (от этого число, разумеется, не меняется) и пользуемся правилом деления дроби на дробь. Примеры на умножение: 0,24∗ В последних четырёх примерах действие идёт не так гладко, как в первых трёх. Умножим, например, Примеры на деление:
В последнем примере сначала превратить целое число с дробью, т.е. Если нужно перемножить несколько дробей, то сначала выписываем над чертою все числители, а под чертою - все знаменатели. Затем всё, что можно, сокращаем. И только после этого перемножаем числа, стоящие над чертою (это будет числитель), и числа, стоящие под чертою (знаменатель).
Вычислим, например, Записываем так:
(сокращаем 8 и 4; 0,25 и 5; 0,034 и 17) =
Вот ещё пример: перемножим Пишем:
(сокращаем 0,121 и 11; 0,15 и 3) =
Примеры:
В последнем примере превратить сначала целое число с дробью в неправильную дробь.
Процентные вычисления В первой главе мы рассмотрели три основные задачи на проценты. Если данные нам числа не так просты, как это было в примерах первой главы, то задачу приходится решать на бумаге. В задачах первого типа даётся число и указывается, сколько процентов от него составляет искомая величина. Найдём, например, 23% от 845. Пишем так: 23% от 845; 23 = 20+3 20% от 845; 1% от 845 = 8,45; 8,45∗3= 25,35 23% от 845 = 169+25,35 = 194,35 Иногда удобнее представлять проценты не в виде суммы, а в виде разности. Найдём, например, 45% от 264. 45% от 264; 45 = 50-5. 50% от 264 = 132 5% от 264 = 13,2 45% от 264 = 132-13,2 = 118,8 В задачах второго типа даются два числа. Требуется узнать, какой процент составляет одно от другого. Узнаем, например, какой процент от 275 составляет 15? Рассуждаем так: 275 составляет 100%, следовательно, 1» (единица в 275 раз меньше, чем 275), а 15 составляет Остаётся вычислить 275 = 100% 1 =
(При переходе от второй дроби к третьей мы сократили на 25.)
В задачах третьего типа данное число составляет некоторый процент от искомого. Решим, например, такую задачу: 72% от некоторого числа составляют 15. Найти само это число. Рассуждаем так же, как в предыдущей задаче. 72% = 15 1% = 100% = Остаётся вычислить
Искомое число:
Рассмотрим задачи на проценты, которые внешне несколько отличаются от трёх основных. Задача 1-я. Сберегательная касса платит по срочным вкладам 5%. Я положил некоторую сумму денег и через год получил 1785 рублей. Какая сумма была положена? Необычность задачи в том, что даётся не сама величина, и не её доля, составляющая данный процент, а сумма самой величины и её доли. Тем не менее простое рассуждение покажет, что перед нами - обычная задача третьего типа. В самом деле, имелась некоторая сумма, составлявшая 100%, да к ней прибавилось 5%. Значит, новая сумма составляет 100+5 = 105%. Дальнейшее просто: 105% = 1785 руб. 1% = 100% = Остаётся вычислить
Задача 2-я. Забраковав 4% продукции, браковщик принял 2592 детали. Сколько всего было изготовлено деталей? Рассуждение такое же, как в предыдущей задаче. Из всей продукции, составляющей 100%, забраковано 4%. Значит, осталось 100-4 = 96%.
Дальнейшее просто: 96% = 2592; 1% = 100% =
(сначала сократили дроби на 12).
Задача 3-я. Население города было 44000, стало 48000 человек. На сколько процентов возросло население? Прежде всего находим прирост населения. Он равен 48000-44000 = 4000. Теперь задача свелась ко второму типу: какой процент составляет 4000 от 44000 (от первоначального числа жителей). 44000 = 100%
Значит, и население города увеличилось на
Задача 4-я. Стахановец, выполнив норму на 420%, обработал 4620 деталей. Сколько деталей обработал он сверх нормы? Несмотря на необычность постановки вопроса, это -обычная задача третьего типа. Только «доля» здесь значительно больше самого числа; но это не влияет на ход рассуждения.
Рассуждаем так: 420% = 4620 деталей 1% = 100% =
Значит норма - 1100 деталей, а сверх нормы 3520 деталей.
Задача 5-я. Я хочу купить бумаги на 100 рублей. Один лист бумаги стоит 80 копеек, и я могу покупать со скидкой в 20%. Сколько листов я могу купить? Рассуждаем так. Узнаем сначала, сколько мне будет стоить один лист. Я уплачу за него не 80 копеек, а только 80% от этого числа (100-20 = 80), то есть
(задача первого типа). Значит, на 100 рублей(=10000 копеек) я могу купить
или, так как части листов не продаются, я могу купить 156 листов, и у меня ещё останется 16 копеек (стоимость Продавец будет считать немного иначе. Если я попрошу его отпустить мне 156 листов, то он будет считать так: 1 лист стоит 80 копеек, 156 листов стоят 80∗16 = 12480 копеек или 124 р. 80 к. С каждой сотни рублей делается скидка в 20 рублей; с 24 р. 80 к. скидка округляется, эта сумма принимается за 25 рублей, и 20% от 25 составляет 5 рублей. Значит, скидка равна 25 рублям, и я уплачу 124 р. 80 к. - 25 р. = 99 р. 80 к., т.е. получу не 16, а 20 копеек сдачи.
Подведём итоги. Имея задачу на проценты, прежде всего, приводим её к одному из трёх основных типов. При этом не смущаемся, если «доля» оказывается больше самой величины. Затем задачи второго и третьего типов решаем «приведением к единице» (это, обычно, проще искусственных приёмов), а в задачах первого типа стараемся так разбить указанное число процентов на слагаемые или вычитаемые, чтобы было легче найти соответствующие им доли.
ГЛАВА III ПРИБЛИЖЁННЫЕ ВЫЧИСЛЕНИЯ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.129.19 (0.06 с.) |
 ;
;  - 0,017;
- 0,017;  ∗0,13;
∗0,13;  :4,6 и т.д. Заметим, что при сложении и вычитании нужно либо все дроби превратить в простые, либо все в десятичные. Удобнее считать, пользуясь десятичными дробями. Поэтому обычно все дроби переводят в десятичные. Особенно удобно это в том случае, если ищется приближённый результат. Если же знаменатели дробей невелики и требуется точный результат, то лучше превращать все десятичные дроби в простые, чтобы не иметь дела с периодическими дробями.
:4,6 и т.д. Заметим, что при сложении и вычитании нужно либо все дроби превратить в простые, либо все в десятичные. Удобнее считать, пользуясь десятичными дробями. Поэтому обычно все дроби переводят в десятичные. Особенно удобно это в том случае, если ищется приближённый результат. Если же знаменатели дробей невелики и требуется точный результат, то лучше превращать все десятичные дроби в простые, чтобы не иметь дела с периодическими дробями.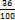 и сокращаем насколько можно; в нашем примере можно сократить на 4. Получаем
и сокращаем насколько можно; в нашем примере можно сократить на 4. Получаем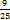 .
.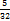 в десятичную дробь. Делим 5 на 32.
в десятичную дробь. Делим 5 на 32.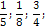

 +
+  + 0,016 =
+ 0,016 =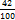 +
+ 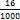 =
=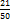 +
+ 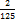 =
=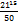 +
+ 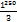 +
+  +
+ 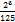 =
=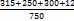 =
= 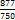 = 1
= 1 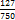 .
. - 0,48 =
- 0,48 = 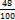 =
= 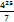 -
- 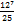 =
= 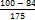 =
= 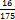
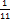 =
= 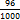 -
- 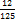 -
- 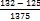 =
= 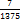 .
. . Пишем:
. Пишем: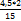 =
= 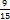 =
=  . Пишем:
. Пишем: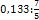 =
= 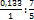 =
= 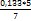 = 0,19∗5 = 0,95
= 0,19∗5 = 0,95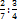 =
= 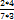 =
= 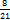
 ; 0,72∗
; 0,72∗ 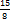 ;
;  ∗0,056;
∗0,056;  ∗0,18; 0,311∗
∗0,18; 0,311∗  ;
; 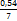 . Сократить ничего нельзя, делить десятичную дробь на 7 - это обрекать себя на бесконечное деление. Поэтому умножаем числитель и знаменатель на 100 - чтоб устранить десятичную дробь в числителе - и получаем -
. Сократить ничего нельзя, делить десятичную дробь на 7 - это обрекать себя на бесконечное деление. Поэтому умножаем числитель и знаменатель на 100 - чтоб устранить десятичную дробь в числителе - и получаем - 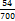 , а по сокращении на 2 - окончательный ответ:
, а по сокращении на 2 - окончательный ответ: 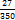 .
.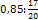 ;
; 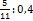 ;
; 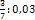 ;
;  ;
;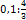 ;
; 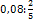 ;
; 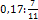 ;
; 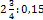 .
.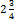 , в неправильную дробь. Два даст
, в неправильную дробь. Два даст 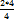 , всего восемь четвёртых, да 3 четвёртых - одиннадцать четвёртых.)
, всего восемь четвёртых, да 3 четвёртых - одиннадцать четвёртых.)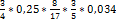 .
. =
= = 0,9∗0,002=0,0018.
= 0,9∗0,002=0,0018. ,
, 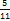 , 0,121,
, 0,121,  и 0,15.
и 0,15.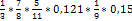 =
= 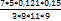 =
= =
= 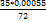 =
= 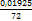 =
= 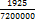 =
= 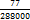 .
.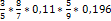 ;
; 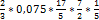 ;
;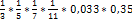 ;
;  .
.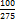 %
%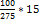 (в 15 раз больше).
(в 15 раз больше).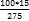 . Записываем:
. Записываем: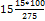 %
% 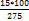 =
= 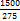 =
= 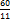 =
= 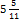 %.
%.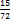 (в 72 раза меньше, чем 72%),
(в 72 раза меньше, чем 72%),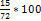 (в 100 раз больше, чем 1%).
(в 100 раз больше, чем 1%).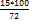 =
= 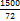 =
= 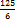 =
= 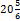
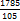 руб. (в 105 раз меньше, чем 105%).
руб. (в 105 раз меньше, чем 105%).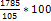 (в 100 раз больше, чем 1%).
(в 100 раз больше, чем 1%).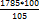 , что даёт 1700 руб.
, что даёт 1700 руб. ;
;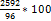
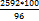 =
= 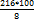 = 27∗100 = 2700 деталей.
= 27∗100 = 2700 деталей.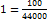 %
% %
%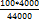 =
= 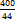 =
= 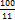 =
= 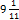 %.
%.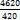 деталей
деталей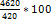 деталей
деталей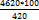 = 1100 деталей.
= 1100 деталей.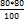 = 64 копейки
= 64 копейки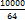 =
= 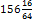 =
= 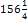 листов
листов листа).
листа).


