
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие случаи умножения и деленияСтр 1 из 10Следующая ⇒
Г.Н. БЕРМАН
ПРИЕМЫ БЫСТРОГО СЧЕТА
ИЗДАНИЕ ВТОРОЕ
ОГИЗ ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ МОСКВА 1947 ЛЕНИНГРАД
Редактор И.Н. Бронштейн. Техн. Редакторы: С.Н. Ахламов Н.А. Тумаркина. Подписано к печ. 22/VIII 1946 г. 4,5 печ. л. 4,1 авт. л. 4,40 уч.-изд. л. 40.000 тип. зн. в печ. л. Тираж 100.000 экз.; А-09861. Цена книги 1 р. 50 к. Зак. №1623.
Набрано в 16-й тип. треста «Полиграфкнига» ОГИЗа при Совете Министров СССР. Москва, Трёхпрудный, 9.
Отпечатано в 3-й типографии «Красный пролетарий» треста «Полиграфкнига» ОГИЗа при Совете Министров СССР. Москва, Краснопролетарская, 16.
Содержание:
ПРЕДИСЛОВИЕ.. 4 ГЛАВА I. УСТНЫЙ СЧЁТ.. 5 1.1. Общие замечания.. 5 1.2. Сложение. 6 1.3. Вычитание. 8 1.4. Простейшие случаи умножения и деления.. 10 1.5. Умножение и деление на 5, 25, 50. Увеличение в 111/2 раза. Умножение на 15 12 1.6. Умножение на 9, 11, 99, 101.. 14 1.7. Умножение на 3, 6 и 7.. 16 1.8. Умножение многозначных чисел.. 17 1.9. Несколько слов о делении в уме. 20 1.10. Проценты... 22 ГЛАВА II. ПИСЬМЕННЫЕ ВЫЧИСЛЕНИЯ.. 25 2.1. О записи чисел.. 25 2.2. Степени десяти.. 26 2.3. Сложение и вычитание. 30 2.4. Умножение и деление на десять и степени десяти. Отрицательные степени десяти 35 2.5. Умножение и деление на однозначное число.. 38 2.6. Умножение многозначных чисел.. 40 2.7. Деление многозначных чисел.. 46 2.8. Вычисления с простыми и десятичными дробями.. 48 2.9. Процентные вычисления.. 54 ГЛАВА III. ПРИБЛИЖЁННЫЕ ВЫЧИСЛЕНИЯ.. 60 3.1. Точные и приближённые значения величин.. 60 3.2. Абсолютная и процентная погрешность.. 63 3.3. Некоторые особенности записи приближённых чисел. Число верных знаков после запятой 66 3.4. Число верных цифр и его связь с процентной погрешностью... 69 3.5. Действия над приближёнными числами. Округление. 71 3.6. Сложение и вычитание приближённых чисел.. 74 3.7. Умножение приближённых чисел.. 77 3.7. Устное умножение приближённых чисел, содержащих по три верные цифры 83 3.9. Деление приближённых чисел.. 85 3.10. Как ставить запятую при приближённом умножении и делении.. 91 3.11. О приближённом извлечении квадратных корней.. 92 3.12. Извлечение корней из чисел с тремя верными цифрами.. 94 3.13. Вычисления по формулам.. 100 3.14. Некоторые формулы приближенных вычислений.. 103
ЗАКЛЮЧЕНИЕ.. 108 ПРЕДИСЛОВИЕ Эта книга не является учебником. Она не претендует ни на полноту, ни на систематичность изложения. Здесь собраны простые приемы, которые помогают ускорить вычисления, ускорить не какие-нибудь сложные расчеты, а самые обычные числовые выкладки, с которыми постоянно приходится иметь дело в быту и, особенно, на производстве. Книга рассчитана на квалифицированного рабочего или техника-практика. Чтение ее не требует никаких специальных знаний, не нужно знать даже элементарной алгебры. Но предполагается, что читатель вполне свободно владеет обычными приёмами счёта с целыми и дробными числами, хотя мог и позабыть всю теорию. Не специальных знаний, но некоторого развития и простых счётных навыков, - вот чего требует эта книжка от читателя. Книга не является учебником. Но, разумеется, если её читать как рассказ, то это будет пустой тратой времени. Математическая книга, даже самая простая, требует работы. Читать её нужно внимательно, с карандашом в руках, выполняя все нужные выкладки и закрепляя каждое понятое правило решением примеров. Примеров в книжке много, но даны они без ответов, так как проверить себя очень легко: достаточно те же приёмы проделать не упрощенным, а обычным путём. Выводов и доказательств в книжке нет. Но там, где это не очень загромождает изложение, даются необходимые объяснения; это помогает успешному усвоению правил. Кое-где терминология немного отличается от обычной. Это иногда позволяет упростить изложение, затруднений же никаких не вызовет. В главе о приближённых вычислениях рассматриваются почти исключительно вычисления с той степенью точности (относительная погрешность в 1%), которая чаще всего требуется при технических расчётах. Автор будет очень благодарен за все критические замечания, поправки и пожелания, о которых читатели захотят ему сообщить. Адрес: Москва, Орликов пер. 3, Гостехиздат.
ГЛАВА I УСТНЫЙ СЧЁТ Общие замечания Каждый из нас умеет считать в уме; в магазинах, в столовых, в трамвае - везде приходится иметь дело со счетом. Особенно важно уметь считать производственнику. Почти ни одна квалифицированная работа не обходится без предварительного подсчета. Одним приходится при этом возиться с карандашом и бумагой; другие считают в уме, но считают медленно, часто ошибаются и сильно устают; наконец, третьи считают легко и уверенно.
Для того чтобы быстро и уверенно считать в уме, не нужно иметь ни специальных знаний, ни способностей. Несколько простых правил, а главное - постоянная тренировка в устном счете, - помогут научиться хорошо считать. Бывают люди, которые быстро множат и делят в уме четырех- и пятизначные числа. Достичь такого искусства трудно, надо помнить много правил, очень долго и утомительно тренироваться. Это искусство в практической жизни почти не может пригодиться. Наша задача - научиться работать с двузначными, иногда - с трехзначными числами. Этого для быта и производственной практики достаточно. Если же встретятся большие числа, то лучше, вернее, сделать вычисления на бумаге. Напомним некоторые арифметические термины. Числа, которые складываются, называются слагаемыми. Результат сложения называется суммой. То число, из которого мы вычитаем, называется уменьшаемым, число, которое мы вычитаем, называется вычитаемым, результат вычитания называется разностью чисел. Возьмем такой пример: 25-7=18. Здесь 25 - уменьшаемое, 7 - вычитаемое, 18 - разность. Числа, которые перемножаются, называются множителями или сомножителями. Иногда один из сомножителей называют множимым, другой - множителем, но такое различие несущественно: и множимое, и множитель совершенно равноправны. Результат умножения называется произведением. То число, которое делят на другое, называют делимым; то число, на которое делят, называют делителем. Результат деления называют частным. Разделим, например, 18 на 6. Получим 3. Здесь 18 - делимое, 6 - делитель, 3 - частное. Не всегда деление проходит так гладко. Поделим, например, 22 на 7. Получим 3 и в остатке единицу. Поделим остаток на 7, найдем одну седьмую. Значит 22:7=3 Сложение Складывать в уме очень легко; и все-таки о сложении нужно сказать несколько слов. Ведь сложение - основное действие, поэтому складывать надо очень быстро и уверенно. Начнем с прибавления однозначного числа. Прибавить 5 к 23 совсем просто: будет 28. Важнее тот случай, когда единицы обоих слагаемых дают в сумме больше десятка и этот десяток нужно держать в уме. Прибавим, например, 8 к 87. Здесь лучше рассуждать так. В восьмидесяти семи не хватает до 90 тройки, а 8 равняется сумме 3 и 5. 87 да 3 - 90, да еще 5 - всего 95. Еще пример: 119+7. семь равно единице плюс шесть; 119 да единица - будет 120, да еще шесть - всего 126. Итак, однозначное слагаемое представляем в виде суммы двух меньших чисел, из которых одно дополняет большее слагаемое до целых десятков. Самая небольшая тренировка приводит к тому, что это разложение выполняется совершенно автоматически, без всякого усилия воли или внимания. Так же прибавляется число, состоящее из целого числа десятков или сотен. Прибавим, например, 50 к 272. Говорим: 272 да 30 даст 302, да еще 20 - всего 322. И здесь разбиваем слагаемое, состоящее из целых десятков, на два (50=30+20), одно из которых (30) дополняет десятки большего слагаемого (70) до целой сотни.
Примеры: 326+9; 148+7; 94+8; 112+6; 243+80; 567+70; 192+20; 341+50; 1460+50; 277+70.
Если оба слагаемых - многозначные числа, то к большему прибавляем сначала старший разряд меньшего, потом - младший разряд. Так, если прибавляется двузначное число, то сначала прибавляют десятки, потом единицы. Сложим, например, 343 и 25. Говорим: 343 да 20 будет 363, да еще 5 - всего 368. Так же поступают при сложении больших чисел. Если нужно сложить 8365 и 376, то рассуждают так: 8365 да 3 сотни, будет 8665, да семь десятков - 8735, да шесть единиц - всего 8741. Отметим случай, когда сложение упрощается. Если одно из слагаемых близко к целому числу десятков или сотен (вообще к «круглому» числу), то рассуждают так: пусть нужно сложить 173 и 59. 59 это 60 без единицы. Прибавляем еще 30 - будет 233, а нам нужно было прибавить 59, значит 1 нужно отнять; получится 232. Точно так же, если к 882 нужно прибавить 197, то говорим так: 197 это 200 без трех. 882 да 200 будет 1082, отнимая 3, получим 1079. Если оба числа близки к «круглым», например, если нужно сложить 98 и 395, то рассуждаем так: 98 - это 100 без двух: 365 - это 400 без пяти. 100 да 400 даст 500; отнимаем 2, будет 498, отнимем еще 5, будет 493. Это и есть искомая сумма. Примеры: 263+25; 384+49; 298+96; 4532+93; 882+161; 766+419; 89+77; 8122+891; 395+88.
Если нужно сложить в уме несколько двузначных чисел, то, обычно сначала складывают все десятки, потом все единицы. Сложим, например, 26, 17, 85 и 43. Рассуждаем так. 20 да 10 будет 30, да еще 80 - будет 110, да 40 - всего 150; запоминаем. 6 и 7 дает 13, да 5 - будет 18, да еще 3 - всего 21. 150 да 21 - всего получится 171. Этот прием всегда быстро ведет к цели. Так же складываются и большие числа, например три или четыре трехзначных числа, но при этом приходится «держать в уме» несколько сумм, так что легко сбиться. Поэтому не тренированному человеку лучше большие числа складывать на счетах или на бумажке. Примеры: 56+13+18; 24+16+14+47; 39+48+13; 11+26+8+44; 58+43+92; 88+75+39. Вычитание При вычитании однозначного числа возможны два случая. Если однозначное число меньше последней цифры уменьшаемого, то действие выполняется совсем просто. Например, отнимем от 28 число 6. Получим 22. Если же однозначное число больше последней цифры уменьшаемого, например, от 42 нужно отнять 7, то удобно рассуждать так. Семь - это 5+2 (2 - последняя цифра уменьшаемого). От 42 отнимаем 2, получим 40; от 40 отнимем 5, получим 35. Так же рассуждаем, если нужно вычесть число, состоящее из целых десятков. Отнимем, например, 90 от 273. Девяносто - это 70+20; отнимаем от 273 семьдесят, - получим 203; отнимаем еще 20, останется 183.
Примеры: 43-8; 58-7; 135-9; 260-40; 52-7; 43-6; 116-8; 116-70; 1003-40.
Если вычитывается двузначное или ещё большее число, то сперва отнимаем сотни (если они есть), потом десятки, потом единицы. Вычтем, например, 27 из 243. От 243 отнимаем 20, остаётся 223. Но 7=4+3 (3 - последняя цифра уменьшаемого). Значит, отнимаем от 223 число 3, остаётся 220; да еще отнимаем 4 - получаем ответ: 216. Можно рассуждать иначе. От 243 хотим отнять 27. Но 27 - это 30 без трёх. Прибавим по 3 и к уменьшаемому и к вычитаемому; от этого результат не изменится. Получим 246 и 30. От 246 отнимаем 30; получаем 216. Этот приём особенно хорош тогда, когда вычитаемое близко к «круглому» числу. Отнимем, например, 296 от 1285. Число 296 меньше трёхсот всего на 4 единицы. Прибавим поэтому и к уменьшаемому, и к вычитаемому по 4. Получим: от 1289 нужно отнять 300=100+200 (в уменьшаемом как раз 2 сотни). От 1289 отнимаем 200 - получается 1089, да ещё отнимаем 100 - получится 989. Это и есть искомый ответ. Примеры: 463-25; 326-83; 561-59; 1020-98; 241-91; 881-95; 624-73; 815-27; 827-39; 111-87; 1063-120; 822-48; 516-123.
Подытожим всё сказанное. Если нужно сложить два числа, то к большему прибавляем меньшее; сначала прибавляем сотни, потом десятки, потом единицы (сначала - старшие разряды, потом - младшие). Если слагаемые (оба или одно) близки к «круглым» числам, то складываем эти «круглые» числа и учитываем нужную поправку. При сложении нескольких двузначных чисел складываем сначала все десятки, потом все единицы и к общему числу десятков прибавляем единицы. Несколько больших чисел (трёхзначных и больших) целесообразнее складывать на бумаге. Если нужно вычесть однозначное число, меньшее последней цифры уменьшаемого или равное ей, то затруднений не возникает. Если нужно вычесть однозначное число, большее последней цифры уменьшаемого, то разбиваем это однозначное число на два (равное последней цифре уменьшаемого и остаток) и вычитаем полученные числа одно за другим. При вычитании двузначных (и многозначных) чисел сначала отнимаем старшие разряды вычитаемого, потом младшие его разряды. Если вычитаемое близко к «круглому» числу, то сперва отнимаем это «круглое» число, а затем делаем поправку. Умножение на 9, 11, 99, 101 Чтобы умножить какое-нибудь число на 9, нужно увеличить его в 10 раз и от полученного результата отнять само данное число. Умножим, например, 87 на 9. Рассуждаем так: 87∗10=870. Остаётся от 870 отнять 87. Но 87 близко к 90 (не хватает трёх единиц). Прибавим к уменьшаемому и вычитаемому по 3: получим 873 и 90. Отнимая 90 от 873, получим 783. Значит, 87∗9=783. Чтобы умножить какое-нибудь число на 11, нужно увеличить его в 10 раз и к полученному результату прибавить само данное число. Возьмём то же, что и в предыдущем примере, число 87 и умножим его на 11. Увеличив 87 в десять раз, получим 870. Прибавим теперь 87. 870 да 80 (80=30+50) даст 950 да еще 7 - 957. Значит, 11∗87=957. Эти правила очень полезны и почти всегда заметно облегчают счёт, но не следует думать, что их нужно применять во всех случаях. Иногда бывает легче умножать попросту. Если, например, число записано с помощью единиц и нулей, то умножаем его на 9 непосредственно. Умножим 101 на 9. Ясно, что получится 909 и никаких специальных правил применять не нужно.
Заметим ещё один приём умножения двузначного числа на 11. Раздвинем цифры двузначного числа и вставим между ними их сумму. Получим нужный результат. Умножим, например, 24 на 11. Раздвигаем цифры 2 и 4 (2...4) и между ними вставляем сумму 2+4=6. Получим 264. Значит, 24∗11=264. Если сумма цифр двузначного числа сама является двухзначной, то её единицы вставляем между цифрами данного числа, а десятки прибавляем к первой цифре. Например, 67 умножаем на 11. Раздвигаем цифры 6 и 7 (6...7) и между ними вставляем 6+7=13. Получим 6 (13) 7. Теперь тройку оставляем на месте, а единицу прибавляем к шести. Получим 737. Значит, 67∗11=737. При небольшом навыке всё это легко делается в уме. Особенно просто умножение двузначного числа на 101. Нужно мысленно приписать справа к данному числу его самого и прочесть то, что получится. Умножим, например, 73 на 101. Пишем (мысленно) 73 и приписываем справа ещё 73. Получим 7373. Это и есть искомый результат: 73∗101=7373. Нетрудно сообразить, как поступать при умножении на 99, Нужно, очевидно, увеличить данное число в 100 раз и от полученного числа отнять само данное число. Если, например, нужно 34 умножить на 99, то сначала умножаем 34 на 100; получим 3400. Теперь от 3400 отнимаем 34. Отнимая 30, получим 3370; отнимая ещё 4, получим 3366. Значит 34∗99=3366. Примеры: 24∗9; 37∗9; 125∗9; 48∗11; 29∗11; 63∗11; 27∗11; 62∗101; 54∗9; 99∗9; 13∗101; 15∗99; 163∗11; 88∗11.
Умножение на 3, 6 и 7 При умножении двузначного числа на 3, на 6 или на 7 сначала умножаем десятки, потом единицы, затем оба результата складываем. Умножим, например, 86 на 3. 80 на 3 даст 240 (3∗8=24), а трижды шесть - 18. 240 да 18 будет 258. Помножим ещё 35 на 7. 30 на 7 - 210, семью пять - 35. 210 да 35 будет 245. Так же выполняется умножение на 6. Трёхзначное число умножается на три по такому же правилу: сперва умножаются сотни, потом - десятки, потом – единицы, потом всё складывается. Умножать по такому же правилу на 6 было бы невыгодно: пришлось бы «держать в уме» большие числа. Лучше сперва умножить данное число на 3, а затем результат удвоить. Умножим, например, 519 на 6. Умножаем сперва 519 на 3. Пятьсот, умноженное на 3, даст 1500; 10, умноженное на 3, даст 30. Всего получается 1530; да ещё 9, умноженное на 3, даст 27. Прибавляем к 1530 это число (27) и получаем 1557. Теперь удваиваем 1557. 1500 дадут при удвоении 3000, а 57 при умножении на 2 даёт 114. Всего получается 3114. Значит, 519∗6=3114. Умножение многозначных чисел на 7 делается тем же приёмом, что и умножение на 3. Но при этом приходится «держать в уме» большие числа; тому, кто не имеет специальной тренировки, лучше умножать многозначные числа на 7 на бумаге. Примеры: 67∗3; 29∗3; 116∗3; 285∗3; 24∗6; 49∗6; 51∗7; 19∗7; 216∗6; 811∗6; 1261∗3; 715∗3; 93∗6; 92∗7; 49∗7; 212∗3; 212∗7; 97∗6. Проценты Процентом называется одна сотая часть данной величины. Если на заводе работает 2000 человек, то 20 человек составляют один процент (записывают: 1%) от всего количества работающих. Трудно представить себе область человеческой деятельности, в которой не пришлось бы иметь дела с процентами. В процентах выражают прирост населения, ход выполнения производственной программы; в процентах ведут учёт соцсоревнования; проценты выплачивают нам сберкассы. Поэтому, очень важно уметь быстро и безошибочно решать задачи, связанные с процентами. Простейшие задачи нужно научиться решать в уме. С процентами связаны три основных вида задач. Прежде всего, задачи, в которых дается некоторая величина и требуется найти другую величину, составляющую от данной указанное число процентов. Во-вторых, задачи, в которых даются две величины, и требуется узнать, сколько процентов от одной из величин составляет вторая. В-третьих, дается некоторое число и указывается, сколько процентов от искомой величины оно составляет; требуется найти саму величину. Прежде чем перейти к разбору этих трёх задач, обратим внимание на таблицу, помещённую на следующей странице. Эта таблица даёт соотношение между числами процентов некоторой величины и соответствующими её долями. Таблицу нужно помнить наизусть, если не целиком, то, во всяком случае, соотношения, отмеченные звёздочками.
Решим теперь задачу первого типа. На заводе 2140 рабочих, из них 30% мужчин. Сколько на заводе работает мужчин? Нужно, очевидно, найти 30% от числа 2140. – Тридцать - это 3∗10. Найдём сначала 10%, т.е. десятую часть. Это будет 214 человек. А 30% - в три раза больше. Умножаем 214 на 3, получаем 642. Значит, на заводе 642 мужчин. Вот ещё пример: норма выработки 225 деталей. Рабочий перевыполнил норму на 16%. Сколько деталей сделал он сверх нормы? Рассуждаем так: 16 это 4 раза 4. Найдём 4% и увеличим то, что получится, в 4 раза. Но 4% - это Переходим к задачам второго типа. У меня было 5 рублей, я израсходовал 3 рубля. Сколько процентов своих денег я израсходовал? Прежде всего, нужно определить, какую долю пяти составляет три. Так как каждый рубль составляет Если мы не запомнили правую половину таблицы (без звёздочек), то рассуждаем так. Каждая пятая часть составляет 20%. Значит, Более сложные задачи этого типа приводят обычно к делению на двузначное число. Мы их рассмотрим во второй главе. В заключение решим задачу третьего типа. В классе 6 отличников, что составляет 20% всего состава класса. Сколько в классе учеников? Рассуждаем так: 20% - это пятая доля. Пятая доля класса состоит из шести учеников. Значит, всего в классе 5∗6=30 учеников. Ещё пример. Забраковано 18 деталей, что составляет 2 Примеры: Найти: 2% от 368, 3% от 720; 5% от 640; 12 Найти: какой процент (вместо «сколько процентов)) часто говорят «какой процент») составляет 8 от 10? 6 от 20? 100 от 1000? 10 от 50? 1 от 8? 9 от 50? 12 от 48? 1/2 от 1? 3 от 75? 10% какой величины равны трём? 5% какой величины равны семи? 25% какой величины равны ГЛАВА II ПИСЬМЕННЫЕ ВЫЧИСЛЕНИЯ О записи чисел Напомним читателям, как записывают целые и дробные числа по десятичной системе. Основное правило состоит в следующем: из двух цифр, стоящих рядом, левая обозначает «единицы» в десять раз больше, чем правая. Если написано целое число (без дроби), то крайняя правая цифра обозначает простые единицы, левее идут десятки, ещё левее - сотни, затем тысячи и т.д. Если имеется целое число с дробью, то целая часть отделяется запятой. Правее запятой идут десятые доли, правее десятых - сотые, ещё правее - тысячные и т.д. Если «единицы» какого-нибудь разряда отсутствуют, то на соответствующем месте ставится нуль. Например, запись 1023,502 обозначает число, содержащее одну тысячу, не содержащее сотен, имеющее два десятка, три единицы, пять десятых долей, не содержащее вовсе сотых долей и имеющее две тысячные доли (читается: тысяча двадцать три целых, запятая, пятьсот две тысячных). Если число не содержит вовсе целой части (такие числа называются правильными дробями), то пишут сначала нуль, потом запятую, а за ней по обычным правилам дробную часть. Например, двадцать семь сотых запишется так: 0,27 (читают: нуль целых, запятая, двадцать семь сотых). Триста четыре десятитысячных - так: 0,0304.
Степени десяти Очень часто приходится иметь дело с числами, имеющими много нулей на конце. Возьмём примеры: 1) Население СССР составляло в 1939 г. 170500000 человек. 2) Расстояние от Земли до Солнца равно 149500000 км. 3) Поверхность всей суши земного шара равна 14900000000 га. Такие числа трудно записывать и читать. Чтобы облегчить запись, используют понятие степени числа. Произведение числа само на себя называют квадратом этого числа. Например, 9=3∗3; значит, 9 есть квадрат трёх. Точно так же 100 есть квадрат десяти. Квадрат тридцати пяти равен 1225 и т.д. Результат перемножения трёх одинаковых сомножителей, равных каждый данному числу, называется кубом данного числа. Например, умножив 2 на 2, получим 4; умножив ещё раз на 2, получим 8; иными словами, 8=2∗2∗2. Говорят, что 8 есть куб числа 2. Точно так же 27 есть куб числа 3 (трижды три - девять, да ещё раз на три - трижды девять - двадцать семь), 1000 есть куб десяти и т.д. С квадратами чисел мы встречаемся при вычислении площадей участков, с кубами - при вычислении объёмов тел. Площадь квадратного участка, сторона которого равна 9 м, будет 9∗9=81 кв.м. Объём комнаты, длина, ширина и высота которой равны по 4 м, будет 4∗4∗4=64 кубометрам. Иногда, приходится перемножать более трёх одинаковых сомножителей. Произведение четырёх одинаковых сомножителей называется четвёртой степенью данного числа, пяти - пятой степенью и т.д. Например, число 81, равное 3∗3∗3∗3, будет четвертой степенью трёх. Произведение 2∗2∗2∗2∗2=32 будет пятой степенью двух. 1000000 будет шестой степенью десяти. Нетрудно сообразить, что всякая степень десяти изобразится единицей с нулями, причём нулей будет столько, какова степень. (Заметим, что квадрат числа называют иначе второй степенью, куб - третьей степенью.) Действительно, 10 в квадрате даст 10∗10=100 (два нуля); 10 в кубе даст 10∗10∗10=1000 (три нуля); 10 в четвёртой степени даст 10∗10∗10∗10=10000 (четыре нуля) и т.д. Любую степень любого числа можно записать как ряд одинаковых чисел, соединённых знаками умножения (пример: 64=2∗2∗2∗2∗2∗2). Но такой способ записи очень громоздок. Поэтому придумали сокращённую запись. Число, которое нужно умножить несколько раз само на себя (его называют основанием степени), пишут только один раз, а справа сверху ставят маленькую цифру, которая показывает, какая степень числа берётся. Например, пишут 53 вместо 5∗5∗5. Пишут 106 вместо 1000000 и т.д. Эта маленькая цифра, показывающая, сколько раз данное число повторяется сомножителем, называется показателем степени. Значит, в нашем примере (106=1000000) миллион будет степенью (шестой степенью) десяти; десять будет основанием; шесть - показателем. Примеры: а) записать без показателей: 24=16; 35=?; 52=?; 73=? б) записать короче с помощью знака показателя: 2∗2∗2∗2∗2∗; 3∗3∗3∗3∗3; 10000000000; 6∗6∗6∗6∗6∗6∗6; 17∗17∗17∗17∗17∗17∗17∗17.
Вернёмся к нашей первой задаче: как сокращённо записать числа с большим числом нулей на конце? Рассмотрим какое-нибудь число такого вида, например 314000000. Мы можем представить это число как произведение двух чисел: числа без нуля на конце и числа, состоящего из единицы с нулями: 314∗1000000. Но вместо «единицы с нулями» мы можем написать степень десяти (в нашем примере - шестую степень), значит: 314000000=314∗106. Вместо креста часто ставят другой знак умножения - точку (пишут 3∙2=6 вместо 3∗2=6). Тогда запись числа с большим числом нулей на конце станет особенно простой: 314000000=314∙106. Запишем в обычной форме и прочитаем число 51∙105. Десять в пятой степени - это «единица с пятью нулями», значит, нужно к пятидесяти одному приписать справа пять нулей: 5100000. Получили пять миллионов сто тысяч. Вернёмся к примерам, помещённым в начале этого параграфа. Мы имели: 1) Население СССР составляло в 1939 г. 170500000 человек. 2) Расстояние от Земли до Солнца равно 149500000 км. 3) Поверхность всей суши земного шара равна 14900000000 га. Эти числа мы запишем теперь так: 1) Население СССР составляло в 1939 г. 1705∙105 человек. 2) Расстояние от Земли до Солнца равно 1495∙105 км. 3) Поверхность всей суши земного шара равна 149∙108 га. Примеры: Записать короче, пользуясь степенями десяти, следующие числа: 180000; 3200000; 43400; 5183000000; 9600000000; 1700000; 20000000. Записать в обычной форме и прочитать следующие числа: 43∙103; 12∙105; 3∙1011; 683∙108; 51342∙102; 1616∙104; 17∙107; 2∙1012; 48∙105; 117∙106.
Сложение и вычитание О сложении и вычитании говорить почти нечего. Общепринятая запись является наиболее удобной. Важно только аккуратно подписывать единицы под единицами, десятки под десятками и т.д. Рекомендуется ставить знаки действий и при вычитании отмечать точкой, когда приходится «занимать» единицу из высшего разряда. Тогда вычисление легко проверить. Примеры:
При сложении многих слагаемых можно вычисления рационализировать. Рассмотрим такой пример:
Складываем числа, как обычно, столбиками, начиная справа, но каждую колонну складываем не подряд, а группируем в ней слагаемые, составляя из них целые десятки. Начинаем с единиц. Три да семь - десять, девять да один - десять, всего двадцать, да два, да один - двадцать три. Три пишем, два помещаем над десятками; эти два да восемь - десять; шесть и четыре - тоже десять, всего двадцать, да восемь, да один, да один - будет тридцать. Нуль пишем, три надписываем над сотнями. Эти три да три, да четыре - десять, восемь и два - ещё десять, всего двадцать, да шесть, да один - всего двадцать семь. Семь пишем, два приписываем к тысячам. Эти два да восемь - десять, четыре да шесть ещё десять - всего двадцать, да пять, да два - двадцать семь. Семь пишем, а два да один, да два дадут пять. При небольшом навыке этот «способ группировки» «или счет на десятки» очень облегчает сложение, позволяет выполнять его быстрее и точнее. Начинающему, чтобы не сбиться, полезно отмечать свои группировки карандашом, как это сделано в нашем примере. Более опытный счётчик обходится и без этого. Если слагаемых много, то полезно выполнять сложение в несколько приёмов, обычно в два.
Пример:
Разбиваем слагаемые на две группы:
Обе полученные суммы складываем:
Последнее число (51169) и будет ответом задачи.
Отметим ещё сложение большого числа близких друг к другу слагаемых. В этом случае записываем не столбиком, а строчкой. Например: 81+83+79+85+78+80+81+77+78=? Заменяем каждое слагаемое ближайшим «круглым» числом (в нашем примере 80) и подписываем у каждого его недостаток или избыток над восьмьюдесятью, недостатки с минусами, избытки с плюсами; недостатки ниже, избытки - выше основной записи. Запись будет выглядеть так:
Подсчитываем, сколько раз повторяется одинаковое число (в нашем примере 80 повторяется 9 раз), перемножаем, прибавляем числа, написанные сверху, отнимаем написанные снизу. Сложение очень большого «столбика» мы заменили простым умножением, которое выполняется в уме.
Примеры:
Деление многозначных чисел При делении полезно обратить внимание на два случая: 1) делимое раскладывается на слагаемые, каждое из которых легко делится на делитель, и 2) делитель разлагается на множители. Рассмотрим эти случаи. Разделим 385 на 35. Имеем 385=350+35. Значит, 385:35=(350+35):35. Триста пятьдесят при делении на 35 даст 10, а тридцать пять при делении само на себя даёт единицу. Всего получаем 11. Значит, 385:35=11. Ещё пример: разделим 2837 на 14. Имеем 2837=2800+28+9. Делим каждое из слагаемых на 14; получаем 200, 2 и 2837:14=(2800+28+9):14=200+2+ Если делим число, близкое к «круглому», легко делящемуся на делитель, то записываем делимое в виде разности двух чисел: «круглого числа» и дополнения. Дальше поступаем, как в предыдущем случае, только результаты не складываем, а вычитаем. Разделим, например, 3104 на 32. Имеем 3104=3200-96. Делим 3200 на 32, получаем 100; делим 96 на 32, получаем 3. Вычитая 3 из 100, получим окончательный ответ: 97. Записываем всё это так: 3104:32=(3200-96):32=100-3=97. Перейдём ко второму случаю. Разделим 4698 на 54. Делитель легко представить как произведение однозначных чисел: 54=6х9. Делить на однозначные числа легко. Поэтому делим наше число на 6, а потом то, что получится, разделим на 9. Располагаем действие так: 4698:54=? 4698:6=783; 783:9=87. Получается значительно проще, чем по обычному правилу деления. Этим мы ограничимся. В остальных случаях вернее и удобнее применять обычное правило деления.
Примеры: 3468:17; 1776:48; 8557:43; 15195:15; 2048:32; 3969:63; 2296:56; 16665:15; 10240:64; 10149:51.
Процентные вычисления В первой главе мы рассмотрели три основные задачи на проценты. Если данные нам числа не так просты, как это было в примерах первой главы, то задачу приходится решать на бумаге. В задачах первого типа даётся число и указывается, сколько процентов от него составляет искомая величина. Найдём, например, 23% от 845. Пишем так: 23% от 845; 23 = 20+3 20% от 845; 1% от 845 = 8,45; 8,45∗3= 25,35 23% от 845 = 169+25,35 = 194,35
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 83; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.159.10 (0.184 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 . Результатом деления целых чисел может быть дробное число (в нашем примере - целое с дробью).
. Результатом деления целых чисел может быть дробное число (в нашем примере - целое с дробью). часть величины. Значит, нужно 225 разделить на 25. Получим 9. Умножив 9 на 4, получим 36. Значит, сверх нормы изготовлено 36 деталей.
часть величины. Значит, нужно 225 разделить на 25. Получим 9. Умножив 9 на 4, получим 36. Значит, сверх нормы изготовлено 36 деталей. от пяти, то три рубля составят
от пяти, то три рубля составят  . Значит, израсходовано три пятых всех денег.
. Значит, израсходовано три пятых всех денег. % всей продукции. Сколько всего было изготовлено деталей? Если 2
% всей продукции. Сколько всего было изготовлено деталей? Если 2  часть всей продукции. Значит, всего было изготовлено 72∗10=720 деталей.
часть всей продукции. Значит, всего было изготовлено 72∗10=720 деталей. ?
?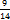 . Все полученные числа складываем: получим 202
. Все полученные числа складываем: получим 202  часть от 845; 845:5=169
часть от 845; 845:5=169


