
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несколько слов о делении в уме
Делить в уме значительно труднее, чем множить. Кроме случаев, упомянутых в начале главы (деление на 2, 4, 5, 25 и т.д.), стоит отметить только деление сравнительно небольших чисел на однозначное число. При этом приходится выполнять в уме те действия, которые мы привыкли делать на бумаге. Разделим, например, 95 на 7. Девять десятков дадут при делении на 7 один десяток, причём два десятка останутся неиспользованными. Эти два десятка да 5 единиц - всего 25 единиц - дадут при делении на 7 в частном 3 и в остатке - 4. Значит, ответ будет: 13 в частном и 4 в остатке, или 13 Примеры: 87:3; 126:3; 59:7; 97:2; 95:3; 147:7; 159:9; 90:11; 116:3; 104:13; 51:3; 91:7; 189:9; 89:9; 1000:3.
В связи с делением стоит вопрос об отыскании той или иной доли данного числа. Действительно, чтобы найти половину какого-нибудь числа, например, 562, достаточно разделить его на 2. В нашем примере получим 281. Чтобы найти одну треть некоторого числа, нужно его разделить на 3. Умея делить в уме на 2, 4, 8, 5, 10, 25, 50, 100, 3, 6, 7, мы можем находить половину, четверть, восьмую, пятую, десятую и другие доли данного числа. Нетрудно найти двадцатую долю некоторого числа: для этого нужно разделить пополам его десятую долю. Найти три четверти какого-нибудь числа можно двумя способами: прежде всего, нужно найти одну четверть числа. Потом одно из двух: или умножить найденную четвертушку на 3, или отнять её от самого числа. Найдём, например, Второй приём годится во всех случаях, когда числитель искомой доли на единицу меньше знаменателя, а первый во всех без исключения случаях. Значит, первый приём более общий, зато второй - в тех случаях, когда он пригоден - немного проще. Вычислим первым приёмом
Вычислим (вторым приёмом) Примеры: Найти Проценты Процентом называется одна сотая часть данной величины. Если на заводе работает 2000 человек, то 20 человек составляют один процент (записывают: 1%) от всего количества работающих. Трудно представить себе область человеческой деятельности, в которой не пришлось бы иметь дела с процентами. В процентах выражают прирост населения, ход выполнения производственной программы; в процентах ведут учёт соцсоревнования; проценты выплачивают нам сберкассы. Поэтому, очень важно уметь быстро и безошибочно решать задачи, связанные с процентами. Простейшие задачи нужно научиться решать в уме. С процентами связаны три основных вида задач. Прежде всего, задачи, в которых дается некоторая величина и требуется найти другую величину, составляющую от данной указанное число процентов. Во-вторых, задачи, в которых даются две величины, и требуется узнать, сколько процентов от одной из величин составляет вторая. В-третьих, дается некоторое число и указывается, сколько процентов от искомой величины оно составляет; требуется найти саму величину. Прежде чем перейти к разбору этих трёх задач, обратим внимание на таблицу, помещённую на следующей странице. Эта таблица даёт соотношение между числами процентов некоторой величины и соответствующими её долями. Таблицу нужно помнить наизусть, если не целиком, то, во всяком случае, соотношения, отмеченные звёздочками.
Решим теперь задачу первого типа. На заводе 2140 рабочих, из них 30% мужчин. Сколько на заводе работает мужчин? Нужно, очевидно, найти 30% от числа 2140. – Тридцать - это 3∗10. Найдём сначала 10%, т.е. десятую часть. Это будет 214 человек. А 30% - в три раза больше. Умножаем 214 на 3, получаем 642. Значит, на заводе 642 мужчин. Вот ещё пример: норма выработки 225 деталей. Рабочий перевыполнил норму на 16%. Сколько деталей сделал он сверх нормы? Рассуждаем так: 16 это 4 раза 4. Найдём 4% и увеличим то, что получится, в 4 раза. Но 4% - это Переходим к задачам второго типа. У меня было 5 рублей, я израсходовал 3 рубля. Сколько процентов своих денег я израсходовал? Прежде всего, нужно определить, какую долю пяти составляет три. Так как каждый рубль составляет Если мы не запомнили правую половину таблицы (без звёздочек), то рассуждаем так. Каждая пятая часть составляет 20%. Значит, Более сложные задачи этого типа приводят обычно к делению на двузначное число. Мы их рассмотрим во второй главе. В заключение решим задачу третьего типа. В классе 6 отличников, что составляет 20% всего состава класса. Сколько в классе учеников? Рассуждаем так: 20% - это пятая доля. Пятая доля класса состоит из шести учеников. Значит, всего в классе 5∗6=30 учеников. Ещё пример. Забраковано 18 деталей, что составляет 2 Примеры: Найти: 2% от 368, 3% от 720; 5% от 640; 12 Найти: какой процент (вместо «сколько процентов)) часто говорят «какой процент») составляет 8 от 10? 6 от 20? 100 от 1000? 10 от 50? 1 от 8? 9 от 50? 12 от 48? 1/2 от 1? 3 от 75? 10% какой величины равны трём? 5% какой величины равны семи? 25% какой величины равны ГЛАВА II ПИСЬМЕННЫЕ ВЫЧИСЛЕНИЯ О записи чисел Напомним читателям, как записывают целые и дробные числа по десятичной системе. Основное правило состоит в следующем: из двух цифр, стоящих рядом, левая обозначает «единицы» в десять раз больше, чем правая. Если написано целое число (без дроби), то крайняя правая цифра обозначает простые единицы, левее идут десятки, ещё левее - сотни, затем тысячи и т.д. Если имеется целое число с дробью, то целая часть отделяется запятой. Правее запятой идут десятые доли, правее десятых - сотые, ещё правее - тысячные и т.д. Если «единицы» какого-нибудь разряда отсутствуют, то на соответствующем месте ставится нуль. Например, запись 1023,502 обозначает число, содержащее одну тысячу, не содержащее сотен, имеющее два десятка, три единицы, пять десятых долей, не содержащее вовсе сотых долей и имеющее две тысячные доли (читается: тысяча двадцать три целых, запятая, пятьсот две тысячных). Если число не содержит вовсе целой части (такие числа называются правильными дробями), то пишут сначала нуль, потом запятую, а за ней по обычным правилам дробную часть. Например, двадцать семь сотых запишется так: 0,27 (читают: нуль целых, запятая, двадцать семь сотых). Триста четыре десятитысячных - так: 0,0304.
Степени десяти Очень часто приходится иметь дело с числами, имеющими много нулей на конце. Возьмём примеры: 1) Население СССР составляло в 1939 г. 170500000 человек. 2) Расстояние от Земли до Солнца равно 149500000 км. 3) Поверхность всей суши земного шара равна 14900000000 га. Такие числа трудно записывать и читать. Чтобы облегчить запись, используют понятие степени числа. Произведение числа само на себя называют квадратом этого числа. Например, 9=3∗3; значит, 9 есть квадрат трёх. Точно так же 100 есть квадрат десяти. Квадрат тридцати пяти равен 1225 и т.д. Результат перемножения трёх одинаковых сомножителей, равных каждый данному числу, называется кубом данного числа. Например, умножив 2 на 2, получим 4; умножив ещё раз на 2, получим 8; иными словами, 8=2∗2∗2. Говорят, что 8 есть куб числа 2. Точно так же 27 есть куб числа 3 (трижды три - девять, да ещё раз на три - трижды девять - двадцать семь), 1000 есть куб десяти и т.д. С квадратами чисел мы встречаемся при вычислении площадей участков, с кубами - при вычислении объёмов тел. Площадь квадратного участка, сторона которого равна 9 м, будет 9∗9=81 кв.м. Объём комнаты, длина, ширина и высота которой равны по 4 м, будет 4∗4∗4=64 кубометрам. Иногда, приходится перемножать более трёх одинаковых сомножителей. Произведение четырёх одинаковых сомножителей называется четвёртой степенью данного числа, пяти - пятой степенью и т.д. Например, число 81, равное 3∗3∗3∗3, будет четвертой степенью трёх. Произведение 2∗2∗2∗2∗2=32 будет пятой степенью двух. 1000000 будет шестой степенью десяти. Нетрудно сообразить, что всякая степень десяти изобразится единицей с нулями, причём нулей будет столько, какова степень. (Заметим, что квадрат числа называют иначе второй степенью, куб - третьей степенью.) Действительно, 10 в квадрате даст 10∗10=100 (два нуля); 10 в кубе даст 10∗10∗10=1000 (три нуля); 10 в четвёртой степени даст 10∗10∗10∗10=10000 (четыре нуля) и т.д. Любую степень любого числа можно записать как ряд одинаковых чисел, соединённых знаками умножения (пример: 64=2∗2∗2∗2∗2∗2). Но такой способ записи очень громоздок. Поэтому придумали сокращённую запись. Число, которое нужно умножить несколько раз само на себя (его называют основанием степени), пишут только один раз, а справа сверху ставят маленькую цифру, которая показывает, какая степень числа берётся. Например, пишут 53 вместо 5∗5∗5. Пишут 106 вместо 1000000 и т.д. Эта маленькая цифра, показывающая, сколько раз данное число повторяется сомножителем, называется показателем степени. Значит, в нашем примере (106=1000000) миллион будет степенью (шестой степенью) десяти; десять будет основанием; шесть - показателем.
Примеры: а) записать без показателей: 24=16; 35=?; 52=?; 73=? б) записать короче с помощью знака показателя: 2∗2∗2∗2∗2∗; 3∗3∗3∗3∗3; 10000000000; 6∗6∗6∗6∗6∗6∗6; 17∗17∗17∗17∗17∗17∗17∗17.
Вернёмся к нашей первой задаче: как сокращённо записать числа с большим числом нулей на конце? Рассмотрим какое-нибудь число такого вида, например 314000000. Мы можем представить это число как произведение двух чисел: числа без нуля на конце и числа, состоящего из единицы с нулями: 314∗1000000. Но вместо «единицы с нулями» мы можем написать степень десяти (в нашем примере - шестую степень), значит: 314000000=314∗106. Вместо креста часто ставят другой знак умножения - точку (пишут 3∙2=6 вместо 3∗2=6). Тогда запись числа с большим числом нулей на конце станет особенно простой: 314000000=314∙106. Запишем в обычной форме и прочитаем число 51∙105. Десять в пятой степени - это «единица с пятью нулями», значит, нужно к пятидесяти одному приписать справа пять нулей: 5100000. Получили пять миллионов сто тысяч. Вернёмся к примерам, помещённым в начале этого параграфа. Мы имели: 1) Население СССР составляло в 1939 г. 170500000 человек. 2) Расстояние от Земли до Солнца равно 149500000 км. 3) Поверхность всей суши земного шара равна 14900000000 га. Эти числа мы запишем теперь так: 1) Население СССР составляло в 1939 г. 1705∙105 человек. 2) Расстояние от Земли до Солнца равно 1495∙105 км. 3) Поверхность всей суши земного шара равна 149∙108 га. Примеры: Записать короче, пользуясь степенями десяти, следующие числа: 180000; 3200000; 43400; 5183000000; 9600000000; 1700000; 20000000. Записать в обычной форме и прочитать следующие числа: 43∙103; 12∙105; 3∙1011; 683∙108; 51342∙102; 1616∙104; 17∙107; 2∙1012; 48∙105; 117∙106.
Сложение и вычитание О сложении и вычитании говорить почти нечего. Общепринятая запись является наиболее удобной. Важно только аккуратно подписывать единицы под единицами, десятки под десятками и т.д. Рекомендуется ставить знаки действий и при вычитании отмечать точкой, когда приходится «занимать» единицу из высшего разряда. Тогда вычисление легко проверить. Примеры:
При сложении многих слагаемых можно вычисления рационализировать. Рассмотрим такой пример:
Складываем числа, как обычно, столбиками, начиная справа, но каждую колонну складываем не подряд, а группируем в ней слагаемые, составляя из них целые десятки. Начинаем с единиц. Три да семь - десять, девять да один - десять, всего двадцать, да два, да один - двадцать три. Три пишем, два помещаем над десятками; эти два да восемь - десять; шесть и четыре - тоже десять, всего двадцать, да восемь, да один, да один - будет тридцать. Нуль пишем, три надписываем над сотнями. Эти три да три, да четыре - десять, восемь и два - ещё десять, всего двадцать, да шесть, да один - всего двадцать семь. Семь пишем, два приписываем к тысячам. Эти два да восемь - десять, четыре да шесть ещё десять - всего двадцать, да пять, да два - двадцать семь. Семь пишем, а два да один, да два дадут пять. При небольшом навыке этот «способ группировки» «или счет на десятки» очень облегчает сложение, позволяет выполнять его быстрее и точнее. Начинающему, чтобы не сбиться, полезно отмечать свои группировки карандашом, как это сделано в нашем примере. Более опытный счётчик обходится и без этого. Если слагаемых много, то полезно выполнять сложение в несколько приёмов, обычно в два.
Пример:
Разбиваем слагаемые на две группы:
Обе полученные суммы складываем:
Последнее число (51169) и будет ответом задачи.
Отметим ещё сложение большого числа близких друг к другу слагаемых. В этом случае записываем не столбиком, а строчкой. Например: 81+83+79+85+78+80+81+77+78=? Заменяем каждое слагаемое ближайшим «круглым» числом (в нашем примере 80) и подписываем у каждого его недостаток или избыток над восьмьюдесятью, недостатки с минусами, избытки с плюсами; недостатки ниже, избытки - выше основной записи. Запись будет выглядеть так:
Подсчитываем, сколько раз повторяется одинаковое число (в нашем примере 80 повторяется 9 раз), перемножаем, прибавляем числа, написанные сверху, отнимаем написанные снизу. Сложение очень большого «столбика» мы заменили простым умножением, которое выполняется в уме.
Примеры:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.162.247 (0.058 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 .
. от 748. Делим 748 на 4. 700 пополам - 350, да 48 пополам - 24, всего 374. Полученное число делим ещё раз пополам: 300 пополам - 150, да 70 пополам - 35 (всего 185), да 4 пополам - 2, всего 187. Это - четвёртая часть. Делая первым способом, умножаем на 3: трижды сто - 300, да трижды 80 – 240 (всего 540), да трижды семь - 21; всего 561. Делая вторым способом, отнимаем найденную четвертушку (187) от самого данного числа (748). Вычитаемое близко к круглому числу (к 200), недостаёт только тринадцати. Прибавляем к уменьшаемому 13, получаем 761; отнимаем двести - остаётся 561.
от 748. Делим 748 на 4. 700 пополам - 350, да 48 пополам - 24, всего 374. Полученное число делим ещё раз пополам: 300 пополам - 150, да 70 пополам - 35 (всего 185), да 4 пополам - 2, всего 187. Это - четвёртая часть. Делая первым способом, умножаем на 3: трижды сто - 300, да трижды 80 – 240 (всего 540), да трижды семь - 21; всего 561. Делая вторым способом, отнимаем найденную четвертушку (187) от самого данного числа (748). Вычитаемое близко к круглому числу (к 200), недостаёт только тринадцати. Прибавляем к уменьшаемому 13, получаем 761; отнимаем двести - остаётся 561. от 344. Находим
от 344. Находим  ; для этого делим 344 на 8. Сначала делим 344 пополам - получаем 172; делим ещё раз пополам - получаем 86, делим ещё раз пополам - получаем 43. Это - одна восьмая доля от 344. А нам нужно 5 таких долей. Остаётся умножить 43 на 5. 43 на 10 - 430. Делим пополам-215. Значит,
; для этого делим 344 на 8. Сначала делим 344 пополам - получаем 172; делим ещё раз пополам - получаем 86, делим ещё раз пополам - получаем 43. Это - одна восьмая доля от 344. А нам нужно 5 таких долей. Остаётся умножить 43 на 5. 43 на 10 - 430. Делим пополам-215. Значит,  от 1449. Одна седьмая от 1449 равна 207 (1449=14 сотен, да ещё 49; 14 сотен дают при делении на 7 две сотни, а сорок девять при делении на семь даёт 7). Остаётся отнять 207 от 1449. Получаем 1242. Это и есть искомая доля.
от 1449. Одна седьмая от 1449 равна 207 (1449=14 сотен, да ещё 49; 14 сотен дают при делении на 7 две сотни, а сорок девять при делении на семь даёт 7). Остаётся отнять 207 от 1449. Получаем 1242. Это и есть искомая доля. от 1035;
от 1035; 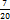 от 5420;
от 5420;  от 3340;
от 3340; 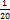 от 837;
от 837;  от 5343;
от 5343;  от 711 (лучше всего поступать так: найти одну треть от 711 и прибавить ее к 711);
от 711 (лучше всего поступать так: найти одну треть от 711 и прибавить ее к 711); 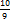 от 387 (как в предыдущем примере);
от 387 (как в предыдущем примере); 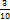 от 6812.
от 6812. часть величины. Значит, нужно 225 разделить на 25. Получим 9. Умножив 9 на 4, получим 36. Значит, сверх нормы изготовлено 36 деталей.
часть величины. Значит, нужно 225 разделить на 25. Получим 9. Умножив 9 на 4, получим 36. Значит, сверх нормы изготовлено 36 деталей. от пяти, то три рубля составят
от пяти, то три рубля составят  . Значит, израсходовано три пятых всех денег.
. Значит, израсходовано три пятых всех денег. % всей продукции. Сколько всего было изготовлено деталей? Если 2
% всей продукции. Сколько всего было изготовлено деталей? Если 2  часть всей продукции. Значит, всего было изготовлено 72∗10=720 деталей.
часть всей продукции. Значит, всего было изготовлено 72∗10=720 деталей. ?
?


