
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные величины. Законы распределения дискретных случайных величин .
Числовые характеристики дискретных случайных величин Дискретной называют случайную величину X, принимающую конечное или счетное (можно перенумеровать) число значений: x 1, x 2, …. Значение Законом распределения случайной величины X называется соответствие vt;le каждым значением Закон распределения обычно задается в виде таблицы, которая называется рядом распределения:
Функция распределения случайной величины
Математическим ожиданием (средним значением) дискретной случайной величины X называется число: M(X)= Если случайная величина принимает счетное число значений, то говорят, что математическое ожидание существует, если ряд Дисперсией случайной величины X называютматематическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Дисперсию удобно вычислять по формуле Средним квадратичным отклонением случайной величины называют квадратный корень из дисперсии:
Среднее квадратичное отклонение является одной из характеристик рассеяния возможных значений случайной величины вокруг ее математического ожидания. Биномиальное распределение. В задачах часто используется биномиальное распределение, то есть распределение случайной величины X – числа наступления события A в n независимых опытах, в каждом из которых событие A может произойти с одной и той же вероятностью p. Случайная величина X принимает целочисленные значения m= 0, 1, …, n с вероятностями
Математическое ожидание, дисперсия и среднее квадратичное отклонение случайной величины X, распределенной по биномиальному закону, находятся по формулам:
где q=1- p. Задания 31-40 31. Закон распределения случайной величины
Вычислить: 32. Закон распределения случайной величины
Вычислить: 33. Закон распределения случайной величины
Вычислить: 34. Закон распределения случайной величины
Вычислить:
35. Закон распределения случайной величины
Вычислить: 36. Закон распределения случайной величины
Вычислить: 37. Закон распределения случайной величины
Вычислить: 38. Закон распределения случайной величины
Вычислить: 39. Закон распределения случайной величины
Вычислить: 40. Закон распределения случайной величины
Вычислить: Пример выполнения заданий 31-40 Случайная величина
Вычислить: Решение. Пусть закон распределения случайной величины представлен в виде
Т.к. закон распределения данной дискретной величины представляет полную группу событий, то сумма всех вероятностей равна 1.
Тогда искомая вероятность:
Математическое ожидание случайной величины находится по формуле:
в нашей задаче
Дисперсия случайной величины:
Чтобы найти
Тогда Отсюда Среднее квадратическое отклонение случайной величины:
тогда
Чтобы найти
Найдем
Для нахождения
Тогда для нашего примера
Чтобы найти
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.113.111 (0.019 с.) |
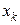 принимается с некоторой вероятностью
принимается с некоторой вероятностью  . При этом
. При этом 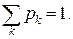
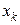 дискретной случайной величины X и ее вероятностью
дискретной случайной величины X и ее вероятностью 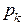 .
.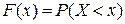 в дискретном случае является кусочно-постоянной и может быть найдена по формуле
в дискретном случае является кусочно-постоянной и может быть найдена по формуле .
.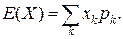
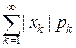 сходится, при расходимости ряда говорят, что математического ожидания не существует.
сходится, при расходимости ряда говорят, что математического ожидания не существует.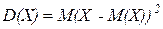 .
.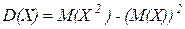 .
.
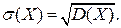
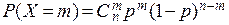 .
. ,
, 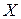 имеет вид:
имеет вид: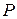

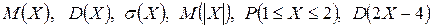 .
.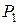
 .
.
 .
.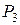
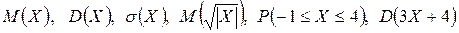 .
. .
.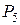
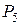 ,
, 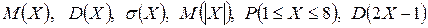 .
.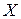
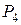
 .
.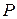
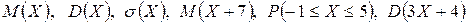 .
.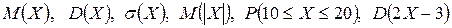 .
.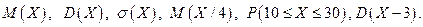
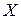 имеет распределение:
имеет распределение: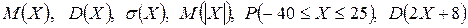 .
.
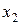
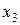
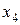
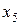
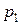

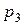
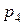
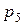
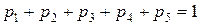 .
.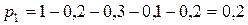 .
. ;
; .
.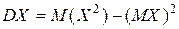 .
.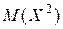 , найдем закон распределения величины
, найдем закон распределения величины 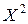 . Для этого возведем все значения, которые принимает
. Для этого возведем все значения, которые принимает  , в квадрат.
, в квадрат. .
. .
.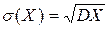 ;
; .
.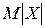 , найдем распределение величины
, найдем распределение величины 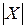 :
: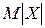 :
: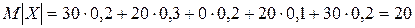 .
.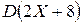 следует знать соотношения:
следует знать соотношения: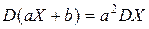 ;
;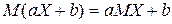 .
.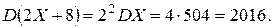
 , следует рассмотреть те значения
, следует рассмотреть те значения 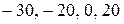 . Этим значениям соответствуют вероятности
. Этим значениям соответствуют вероятности 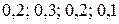 . События, состоящие в том, что
. События, состоящие в том, что 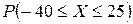 равна сумме вероятностей:
равна сумме вероятностей: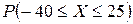
 .
.


