
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема сложения для совместных событий
Два события называют совместными, если появление одного из них не исключает появление другого в одном и том же испытании. Пусть события A и B совместны, известны вероятности этих событий и вероятность их совместного появления. Теорема (сложения совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Задани я 1 - 10. (в него входит шесть задач). 1. Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта. 2. Определить испытания и элементарные события. 3. Определить исследуемое событие А и другие события. 4. Установить, какие формулы следует использовать для вычислений и выполнить последние. Задание 1.1. Бросают две монеты. Найти вероятность того, что: 1) на обеих монетах появится «герб»; 2) хотя бы на одной монете появится «герб»; 3) ни на одной монете не появится «герб»; Бросают три монеты. Найти вероятность того, что: 4) на всех монетах появится «герб»; 5) хотя бы на одной монете появится «герб»; 6) только на двух монетах появится «герб»; 7) только на одной монете появится «герб»; 8) ни на оной монете не появится «герб»; Бросают четыре монеты. Найти вероятность того, что: 9) на всех монетах появится «герб»; 10) хотя бы на одной монете появится «герб». Задание 1.2. Слово составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что буквы вынимаются в порядке заданного слова. Слова по вариантам: 1) ПРОГРАММА. 2) ПРОГРАММИСТ. 3) ПРОГРАММИРОВАНИЕ. 4) СТАТИСТИК. 5) СТАТИСТИКА. 6) СОБЫТИЕ. 7) СЛУЧАЙНОСТЬ. 8) ВЕРОЯТНОСТЬ. 9) АЛГОРИТМ. 10) БЛОК-СХЕМА. Задание 1.3. Как и в предыдущей задаче, найти соответствующую вероятность случая, когда заданным словом является ваша фамилия и ваше имя. Задание 1.4. В урне содержится К черных и Н белых шаров. Случайным образом вынимают М шаров. Найти вероятность того, что среди них имеется: б) меньше, чем Р, белых шаров; в) хотя бы один белый шар. Значения параметров К, Н, М и Р по вариантам приведены в табл. 1. Табл. 1.
Задание 1.5. Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностью р 1, р 2, р 3. Найти вероятность того, что за время Т выйдет из строя:
а). только один элемент; б) хотя бы один элемент. Значения параметров вычислить по следующим формулам:
(Здесь V – номер Вашего варианта.) Задание 1.6. В первой урне К белых и L черных шаров, а во второй – M белых и N черных. Из первой урны вынимают случайным образом Р шаров, а из второй – Q шаров. Найти вероятность того, что среди вынутых шаров: а). все шары одного цвета; б). только три белых шара; в). хотя бы один белый шар. Значения параметров К, L, M, N, Р и Q приведены в таблице 2 по вариантам. Табл.2.
Пример выполнения заданий 1-10 Задание 1.1. Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на 5. Определим испытание и его результат, т.е. элементарное событие. Испытанием бросание трех игральных костей, результатом – одно из сочетаний очков на верхних гранях трех костей. Исследуемое событие А – сумма очков на трех верхних гранях делится на 5. Вероятность события А находится по формуле: Общее количество элементарных событий n можно найти по правилу умножения. На каждой игральной кости 6 граней, и все они могут сочетаться со всеми гранями других костей. Итак, получаем:
Количество элементарных событий m, входящих в состав события А, или благоприятствующих событию А, найдем, выписав все возможные результаты испытаний, и оставив из них только те, для которых сумма очков на всех трех костях делится на 5. Имеем:
В результате получим, что m= 43. Следовательно, искомая вероятность:
Задание 1.2. Слово «МАТЕМАТИКА» составлено из карточек, на каждой из которых написана только одна буква. Затем карточки перемешивают и вынимают без возврата по одной. Найти вероятность случая, что буквы появятся в порядке заданного слова. Испытание заключается в вынимании карточек с буквами в случайном порядке без возврата. Элементарным событием является полученная последовательность букв. Событие А состоит в получении нужного слова «МАТЕМАТИКА». Так как элементарные события являются перестановками из 10 букв, то
Таким образом,
Задание 1.3. (решается аналогично задаче 1.2). Задание 1.4. В урне 5 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется: а) 2 белых шара; б) меньше, чем 2 белых шара; в) хотя бы один белый шар. Испытанием будет случайное вынимание 4 шаров. Элементарными событиями являются всевозможные сочетания по 4 из 11 шаров. Их число равно:
а)
б) В 1 – среди вынутых шаров 1 белый и 3 черных шара; В 2 - все вынутые шары – черные. Следовательно,
в) В 1 – среди вынутых шаров 1 белый и 3 черных шара; В 2 - среди вынутых шаров 2 белый и 2 черных шара; В 3 - среди вынутых шаров 3 белых и 1 черный шар; В 4 - среди вынутых шаров 4 белых шара. Прямое решение этой задачи приводит обычно к сложным вычислениям. Проще сначала найти вероятность противоположного события, а затем вычислить вероятность искомого.
Тогда Ответ: Задание 1.5. Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями 0,851, 0,751, 0,701. Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент. Испытание, т.е. работу за время Т, нужно рассмотреть на двух уровнях: на уровне устройства и на уровне элементов. Элементарные события определять не надо, так как их вероятности заданы. а)
Учитывая независимость элементов устройств, несовместность событий
По условию,
Тогда
Следовательно, получаем:
б) Так как событие определяется словами «хотя бы один», используем противоположное событие:
Ответ: Задание 1.6. В первой урне 6 белых и 4 черных шара, а во второй 5 белых и 7 черных шаров. Из первой урны взяли 3 шара наугад, а из второй – 2 шара. Найти вероятность того, что среди вынутых шаров:
а) все шары одного цвета; б) только 3 белых шара; в) хотя бы один белый шар. Шары вынимали из обеих урн независимо. Испытаниями являются извлечение трех шаров из первой урны и двух шаров из второй. Элементарными событиями будут сочетания по 3 или 2 из 10 или 12 шаров соответственно. а)
Таким образом,
Найдем количество элементарных событий
Найдем количество каждого из элементарных событий, определяющих следующие события:
Следовательно,
б)
в)
Тогда: Ответ:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.111.125 (0.043 с.) |
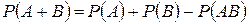 .
.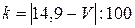 ,
, 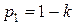 ,
, 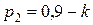 ,
, 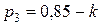 .
.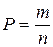 .
. .
.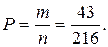
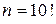 Некоторые буквы в слове «МАТЕМАТИКА» повторяются (М – 2 раза, А – 3 раза, Т – 2 раза). Поэтому возможны перестановки, при которых слово не меняется. Их число равно:
Некоторые буквы в слове «МАТЕМАТИКА» повторяются (М – 2 раза, А – 3 раза, Т – 2 раза). Поэтому возможны перестановки, при которых слово не меняется. Их число равно:  =24.
=24.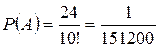 .
.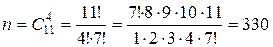 .
.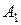 - среди вынутых шаров 2 белых. Значит, среди вынутых шаров – 2 белых и 2 черных (т.к. вынимают 4). Используя правило умножения, получаем:
- среди вынутых шаров 2 белых. Значит, среди вынутых шаров – 2 белых и 2 черных (т.к. вынимают 4). Используя правило умножения, получаем: ,
, 
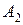 - среди вынутых шаров меньше, чем 2 белых. Это событие состоит из двух несовместных событий:
- среди вынутых шаров меньше, чем 2 белых. Это событие состоит из двух несовместных событий: .
.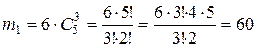 ,
, 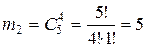 .
.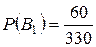 ;
;  ;
; 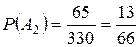 .
.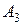 - среди вынутых шаров хотя бы один белый. Этому событию удовлетворяют следующие сочетания шаров:
- среди вынутых шаров хотя бы один белый. Этому событию удовлетворяют следующие сочетания шаров: - среди вынутых шаров нет ни одного белого. В этом случае
- среди вынутых шаров нет ни одного белого. В этом случае ;
; 
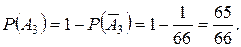
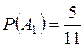 ;
; 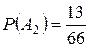 ;
; 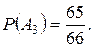
 - первый элемент выходит из строя;
- первый элемент выходит из строя;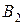 - второй элемент выходит из строя;
- второй элемент выходит из строя;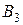 - третий элемент выходит из строя;
- третий элемент выходит из строя; - первый элемент не выходит из строя;
- первый элемент не выходит из строя;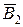 - второй элемент не выходит из строя;
- второй элемент не выходит из строя; - третий элемент не выходит из строя.
- третий элемент не выходит из строя.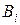 и
и 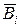 , получаем следующую формулу:
, получаем следующую формулу: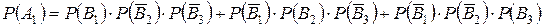 .
.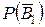 = 0,851,
= 0,851, 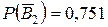 ,
, 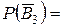 0,701.
0,701.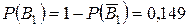 ,
,  ,
, .
.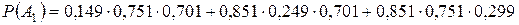 =0,418.
=0,418. - за время Т все элементы работают безотказно.
- за время Т все элементы работают безотказно.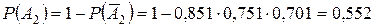 .
.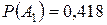 ,
, 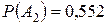 .
. - из первой урны вынуты 3 черных шара;
- из первой урны вынуты 3 черных шара;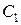 - из второй урны вынуты 2 белых шара;
- из второй урны вынуты 2 белых шара;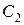 - из второй урны вынуты 1 белый и 1 черный шар;
- из второй урны вынуты 1 белый и 1 черный шар;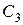 - из второй урны вынуты 2 черных шара.
- из второй урны вынуты 2 черных шара.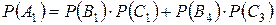 .
.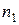 и
и 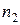 для первой и второй урн соответственно. Имеем:
для первой и второй урн соответственно. Имеем: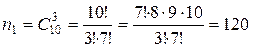 ,
, 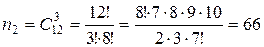 .
.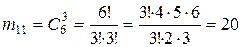 ,
,  ,
,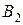 :
: 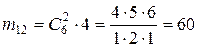 ,
,  ,
,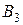 :
: 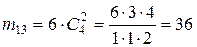 ,
, 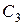 :
: 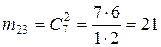 ,
,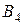 :
: 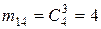 .
.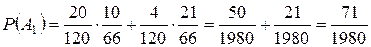 .
.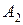 - среди извлеченных шаров только 3 белых. В этом случае:
- среди извлеченных шаров только 3 белых. В этом случае: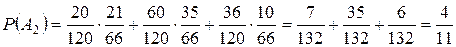 .
.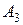 - среди извлеченных шаров имеется по крайней мере один белый.
- среди извлеченных шаров имеется по крайней мере один белый. ,
, 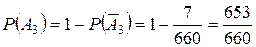 .
.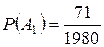 ,
,  ,
, 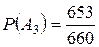 .
.


