Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические оценки параметров распределения. Метод моментов оценки параметров
Пусть Оценкой (статистикой) Оценка В противном случае оценка называется смещенной. Можно показать, что выборочное среднее
является несмещенной оценкой теоретической дисперсии. Состоятельной называют статистическую оценку, которая при неограниченном увеличении числа наблюдений стремится по вероятности к оцениваемому параметру: Можно показать, что оценки Несмещенная оценка Рассмотрим основные методы получения оценок. Метод моментов. Пусть имеется выборка Суть метода моментов заключается в следующем: эмпирические моменты являются оценками соответствующих теоретических моментов, поэтому теоретические моменты Таким образом, в методе моментов оценки
В таблице ниже приведены формулы для вычисления эмпирических и соответствующих им теоретических моментов порядка k. Таблица 7 – Эмпирические и теоретические моменты
Метод максимального правдоподобия. Пусть имеется выборка Основу метода составляет функция правдоподобия:
В дискретном случае функция В абсолютно непрерывном случае функция Согласно методу максимального правдоподобия в качестве оценки неизвестных параметров Нахождение оценок может упрощаться, если максимизировать не саму функцию L, а Задания 8 1 – 9 0 Выборка представлена интервалами и частотами попаданий в эти интервалы. Найти середины интервалов и частости. Допуская, что генеральная совокупность имеет нормальный закон распределения
1) оценить методом моментов параметры а и 2) сравнив результаты графически, построить на одном рисунке гистограмму частостей и соответствующую кривую плотности распределения. 81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
Пример выполнения заданий 81-90 Случайная величина Х (отклонение контролируемого размера изделия
Таблица 8
Методом моментов найти точечные оценки неизвестных параметров Решение. Найдем начальный эмпирический момент первого порядка и центральный эмпирический момент второго порядка. Согласно формулам из таблицы 7:
Эмпирический момент второго порядка – это выборочная дисперсия, которую рассчитаем по формуле:
Таким образом,
Составляем систему уравнений:
В нашем случае
Таким образом, Точечные оценки неизвестных параметров Плотность нашего распределения имеет вид:
Чтобы убедиться в правильности нашего решения, подставим в полученную формулу значения х и найдем значения Таблица 9
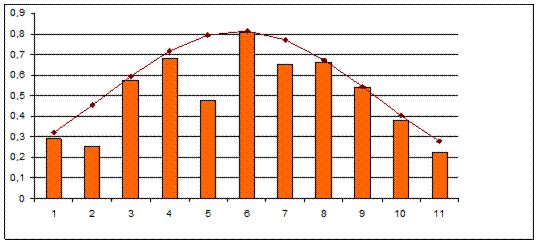
Построим гистограмму относительных частот и график полученной функции распределения:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.186.72 (0.021 с.) |
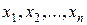 - выборка из теоретического распределения
- выборка из теоретического распределения 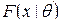 , зависящего от неизвестного параметра
, зависящего от неизвестного параметра 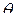 .
.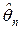 неизвестного параметра
неизвестного параметра 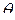 называется любая борелевская функция от наблюдаемых случайных величин.
называется любая борелевская функция от наблюдаемых случайных величин.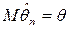 .
.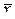 является несмещенной оценкой теоретического математического ожидания, а выборочная дисперсия
является несмещенной оценкой теоретического математического ожидания, а выборочная дисперсия 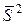 является смещенной оценкой теоретической дисперсии. Исправленная выборочная дисперсия
является смещенной оценкой теоретической дисперсии. Исправленная выборочная дисперсия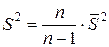
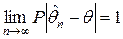 .
.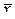 ,
, 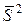 и
и 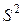 являются состоятельными оценками теоретического математического ожидания и теоретической дисперсии соответственно.
являются состоятельными оценками теоретического математического ожидания и теоретической дисперсии соответственно.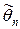 – произвольная несмещенная оценка параметра, а
– произвольная несмещенная оценка параметра, а 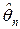 – эффективная, то
– эффективная, то 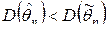 .
.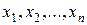 из распределения
из распределения 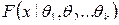 , зависящего от неизвестных параметров
, зависящего от неизвестных параметров 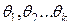 , которые нужно оценить. Поскольку известен вид теоретической функции распределения, можем вычислить первые k теоретических моментов (начальных или центральных). Эти моменты будут зависеть от k неизвестных параметров
, которые нужно оценить. Поскольку известен вид теоретической функции распределения, можем вычислить первые k теоретических моментов (начальных или центральных). Эти моменты будут зависеть от k неизвестных параметров 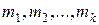 приравнивают к соответствующим эмпирическим
приравнивают к соответствующим эмпирическим 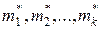 , а затем, решая систему относительно
, а затем, решая систему относительно 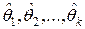 неизвестных параметров
неизвестных параметров 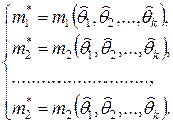
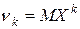
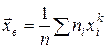
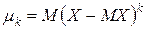
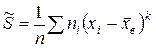
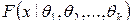 , зависящего от неизвестных параметров
, зависящего от неизвестных параметров 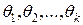 которые нужно оценить.
которые нужно оценить.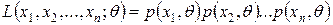 .
.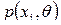 выражает вероятность того, что теоретическая случайная величина примет значение
выражает вероятность того, что теоретическая случайная величина примет значение 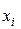 ,
, 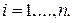
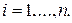
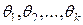 принимаются такие значения
принимаются такие значения 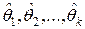 , которые максимизируют функцию правдоподобия.
, которые максимизируют функцию правдоподобия.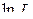 .
.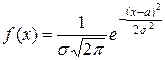 ,
,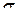 ;
;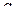 и
и 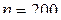 изделий (в первой строке указано отклонение
изделий (в первой строке указано отклонение 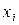 (мм), во второй строке приведена частота
(мм), во второй строке приведена частота 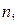 - количество изделий, имеющих отклонение
- количество изделий, имеющих отклонение 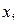 ):
):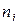

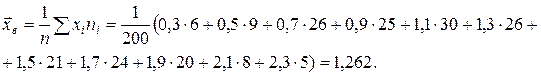
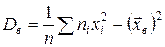 .
.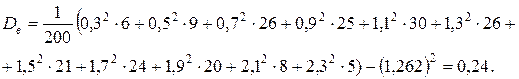
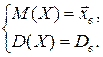
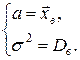
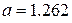 ,
, 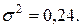
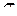 нормального распределения
нормального распределения 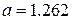 ,
, 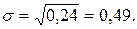
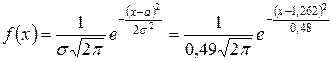 .
.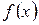 :
: