
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотез о виде распределения
На основе собранных в статистических исследованиях данных после их обработки делаются выводы об изучаемых явлениях. Эти выводы делаются путём выдвижения и проверки статистических гипотез. Статистической гипотезой называется любое утверждение о виде или свойствах распределения наблюдаемых в эксперименте случайных величин. Статистические гипотезы проверяются статистическими методами. Проверяемая гипотеза называется основной (нулевой) и обозначается Н 0. Кроме нулевой выдвигается ещё и альтернативная (конкурирующая) гипотеза Н 1,отрицающая основную. Таким образом, в результате проверки будет принята одна и только одна из гипотез, а вторая будет отвергнута. Выдвинутая гипотеза проверяется на основании исследования выборки, полученной из генеральной совокупности. Из-за случайности выборки в результате проверки не всегда делается правильный вывод. При этом могут возникать следующие ситуации: 1. Основная гипотеза верна и она принимается. 2. Основная гипотеза верна, но она отвергается. 3. Основная гипотеза не верна и она отвергается. 4. Основная гипотеза не верна, но она принимается. В случае 2 говорят об ошибке первого рода, в последнем случае речь идёт об ошибке второго рода. Таким образом, по одним выборкам принимается правильное решение, а по другим – неправильное. Решение принимается по значению некоторой функции выборки, называемой статистической характеристикой, статистическим критерием или просто статистикой. Множество значений этой статистики можно разделить на два непересекающихся подмножества: § подмножество значений статистики, при которых гипотеза Н 0принимается (не отклоняется), называется областью принятия гипо тезы (допустимой областью); § подмножество значений статистики, при которых гипотеза Н 0 отвергается (отклоняется) и принимается гипотеза Н 1,называется критической областью. Основная гипотеза Н 0 о значении неизвестного параметра q распределения обычно выглядит так: Н 0: q = q 0. Конкурирующая гипотеза Н 1может при этом иметь следующий вид: Н 1: q < q 0, Н 1: q > q 0 или Н 1: q ¹ q 0. Соответственно получается левосторонняя, правосторонняя или двусторонняя критические области. Граничные точки критических областей (критические точки) определяют по таблицам распределения соответствующей статистики.
При проверке гипотезы разумно уменьшить вероятность принятия неправильных решений. Допустимая вероятность ошибки первого рода обозначается обычно a и называется уровнем значимости. Его значение, как правило, мало (0,1, 0,05, 0,01, 0,001 …). Но уменьшение вероятности ошибки первого рода приводит к увеличению вероятности ошибки второго рода (b), т.е. стремление принимать только верные гипотезы вызывает возрастание числа отброшенных правильных гипотез. Поэтому выбор уровня значимости определяется важностью поставленной проблемы и тяжестью последствий неверно принятого решения. Проверка статистической гипотезы состоит из следующих этапов: 1) определение гипотез Н 0и Н 1; 2) выбор статистики и задание уровня значимости; 3) определение критических точек Ккр и критической области; 4) вычисление по выборке значения статистики Кэкс; 5) сравнение значения статистики с критической областью (Ккр и Кэкс); 6) принятие решения: если значение статистики не входит в критическую область, то принимается гипотеза Н 0 и отвергается гипотеза H 1, а если входит в критическую область, то отвергается гипотеза Н 0 и принимается гипотеза Н 1. При этом, результаты проверки статистической гипотезы нужно интерпретировать так: если приняли гипотезу Н 1, то можно считать её доказанной, а если принялигипотезу Н 0, то признали, что она не противоречит результатам наблюдений.Однако этим свойством наряду с Н 0могут обладать и другие гипотезы. На основании выборки из генеральной совокупности или из каких-то иных соображений выдвигается нулевая гипотеза о конкретном распределении генеральной совокупности, выраженной через функцию распределения F (x). Это распределение назовём теоретическим. По выборке находится эмпирическая функция распределе ния F * (x). Гипотеза Н 0 о распределении генеральной совокупности принимается, если эмпирическое распределение хорошо согласуется с теоретическим. Задания 111-120 На основании данных заданий 61-70 проверьте гипотезу о нормальном распределении по данной выборке. Уровень значимости a = 0,05.
Пример выполнения заданий 111 – 120 Проверим гипотезу о том, что распределение масс является нормальным. Выдвинем основную и альтернативную гипотезы: H 0: распределение масс является нормальным; H 1: распределение масс не является нормальным. Прежде всего, объединяем крайние интервалы с соседними (см. таблицу 1), т.к. их эмпирические частоты mi меньше 4. Данные заносим в таблицу 2 (столбец mi), причём первый интервал начинаем с –¥, а последний интервал заканчиваем +¥. Считая, что данное распределение является нормальным с математическим ожиданием 80,0 мг и средним квадратическим отклонением 32,34 мг, при помощи таблицы значений функции Лапласа (приведены в приложениях) вычисляем вероятности попадания в соответствующий интервал pi:
Умножаем эти вероятности на объём выборки (n = 140) и получаем теоретические частоты (mi ’). Заполняем два оставшихся столбца и находим суммы по столбцам. Таблица 10.
Последняя сумма соответствует искомому критерию Данная выборка разбита на l = 7 интервалов. В нормальном распределении р = 2 подбираемых параметра (математическое ожидание и среднее квадратическое отклонение). Поэтому число степеней свободы в данном случае k = l - p - 1 = 7 - 2 - 1 = 4. При уровне значимости a = 0,05 и найденному числу степеней свободы из таблицы критических точек распределения c 2 находим значение критерия Т.к. Задания 12 1- 130 По заданной выборке проверить гипотезу о виде распределения. 121. Для статистического анализа были получены следующие результаты: 2; 4; 5; 2; 4; 3; 6; 3; 4; 4; 3; 4; 2; 2; 2; 4; 3; 3; 1; 2; 5; 2; 6; 5; 4; 4; 1; 3; 2; 4; 4; 2; 4; 5; 4; 3; 4; 4; 3; 5; 5; 1; 4; 4; 6; 2; 5; 5; 4; 0; 4; 5; 1; 4; 3; 4; 3; 3; 3; 4; 2; 4; 3; 5; 2; 1; 4; 4; 3; 4; 3; 2; 3; 1; 3; 1; 3; 3; 4; 5; 3; 3; 5; 4; 4; 5; 4; 6; 4; 2; 3; 5; 4; 3; 3; 3; 5; 4; 3; 4; 2; 4; 3; 3; 4; 4; 4; 3; 5; 4; 5; 6; 4; 4; 6; 3; 3; 4; 3; 1; 2; 5; 5; 5; 2; 4; 2; 4; 2; 2; 2; 5; 6; 4; 2; 3; 1; 5; 4; 5; 0; 3; 4; 3; 6; 4; 3; 1; 5; 4; 4; 5; 2; 2; 5; 3; 5; 5; 6; 4; 4; 3; 3; 4; 3; 5; 5; 3; 5; 2; 4; 4; 4; 2; 3; 3; 5; 5; 5; 4; 4; 4; 4; 2; 5; 3; 4; 3; 4; 3; 3; 3; 3; 4; 5; 4; 5; 5; 3; 2. Проверьте гипотезу о биномиальном распределении по данной выборке. Уровень значимости a = 0,1. Объем выборки n = 200. 122. Для статистического анализа были получены следующие результаты: 2; 0; 2; 2; 4; 0; 2; 3; 2; 3; 7; 3; 0; 0; 3; 3; 1; 6; 3; 4; 5; 3; 4; 5; 3; 6; 4; 2; 4; 2; 3; 2; 2; 3; 3; 2; 3; 2; 2; 1; 4; 7; 3; 2; 5; 2; 3; 3; 0; 6; 3; 2; 2; 6; 5; 1; 2; 4; 5; 5; 3; 2; 1; 4; 3; 2; 1; 5; 1; 4; 2; 3; 4; 2; 6; 2; 4; 2; 5; 5; 5; 3; 3; 2; 1; 2; 0; 4; 5; 1; 2; 0; 1; 5; 1; 2; 3; 0; 2; 3; 2; 3; 2; 0; 2; 3; 0; 8; 4; 1; 2; 3; 8; 2; 6; 3; 5; 2; 0; 3; 2; 4; 3; 6; 6; 5; 2; 3; 1; 4; 6; 1; 4; 3; 5; 2; 3; 0; 3; 1; 1; 1; 2; 3; 5; 3; 5; 1; 3; 2. Проверьте гипотезу о том, что данная выборка имеет распределение Пуассона. Уровень значимости a = 0,05. Объем выборки n = 150. 123. Для статистического анализа были получены следующие результаты: 3; 3; 5; 3; 5; 4; 4; 2; 2; 4; 1; 2; 1; 1; 1; 1; 4; 5; 1; 2; 1; 2; 6; 2; 6; 5; 3; 1; 1; 1; 3; 5; 3; 5; 5; 6; 3; 2; 3; 5; 6; 1; 1; 1; 1; 3; 2; 2; 4; 3; 4; 1; 2; 5; 1; 2; 6; 3; 2; 4; 3; 4; 2; 6; 4; 5; 1; 1; 2; 3; 2; 2; 3; 1; 5; 6; 5; 4; 3; 5; 6; 3; 5; 3; 5; 3; 6; 3; 2; 6; 5; 6; 5; 1; 2; 1; 2; 6; 1; 6; 4; 4; 6; 6; 1; 4; 6; 3; 1; 1; 1; 3; 4; 2; 4; 6; 4; 5; 1; 3; 6; 4; 2; 4; 5; 1; 4; 2; 1; 5; 3; 1; 2; 5; 3; 1; 6; 6; 4; 4; 3; 5; 3; 5; 3; 4; 4; 3; 3; 5. Проверьте гипотезу о равномерном дискретном распределении рассматриваемой величины по данной выборке. Уровень значимости a = 0,05. Объем выборки n = 150.
124. Для статистического анализа были получены следующие результаты: 7; 5; 6; 7; 6; 8; 7; 6; 8; 5; 7; 5; 6; 7; 6; 7; 8; 7; 4; 6; 6; 7; 5; 5; 7; 5; 7; 4; 5; 7; 6; 5; 4; 5; 5; 4; 5; 6; 5; 6; 6; 7; 3; 5; 5; 4; 7; 5; 6; 8; 8; 7; 6; 6; 7; 6; 3; 6; 7; 6; 4; 4; 7; 4; 7; 3; 6; 6; 7; 6; 5; 6; 5; 6; 4; 3; 7; 7; 2; 7; 6; 6; 7; 7; 5; 5; 6; 6; 5; 4; 6; 5; 3; 6; 8; 7; 5; 6; 7; 8; 6; 5; 7; 4; 4; 7; 8; 3; 7; 5; 7; 6; 4; 6; 5; 7; 5; 5; 6; 7; 7; 7; 6; 4; 6; 4; 5; 7; 8; 5; 5; 7; 5; 3; 5; 3; 5; 7; 5; 5; 1; 7; 5; 7; 7; 5; 6; 5; 3; 5; 3; 6; 3; 5; 6; 5; 7; 8; 5; 5; 8; 6; 6; 6; 8; 4; 4; 6; 6; 8; 7; 5; 6; 7; 6; 6; 6; 6; 6; 5; 8; 6; 4; 6; 7; 6; 7; 5; 3; 6; 7; 6; 6; 5; 6; 4; 6; 5; 4; 7; 6; 7; 7; 6; 5; 7; 5; 4; 7; 6; 3; 5; 5; 6; 5; 5; 8; 3; 5; 4. Проверьте гипотезу о биномиальном распределении рассматриваемой величины по данной выборке. Уровень значимости a = 0,1. Объем выборки n = 220. 125. 2; 4; 0; 3; 3; 5; 0; 6; 2; 2; 2; 3; 5; 1; 5; 1; 6; 4; 4; 4; 6; 6; 1; 7; 5; 3; 4; 0; 4; 5; 2; 4; 1; 2; 4; 8; 2; 3; 5; 3; 2; 1; 2; 2; 2; 5; 3; 5; 4; 6; 2; 6; 5; 4; 1; 2; 3; 4; 4; 4; 2; 6; 4; 3; 5; 1; 5; 5; 4; 4; 3; 3; 1; 2; 4; 2; 4; 4; 6; 4; 2; 6; 7; 4; 0; 7; 3; 6; 2; 5; 3; 7; 4; 1; 2; 5; 7; 4; 4; 3; 3; 4; 3; 2; 3; 2; 3; 3; 4; 2; 2; 3; 2; 2; 4; 0; 7; 2; 5; 0; 6; 4; 4; 4; 3; 6; 4; 1; 2; 1; 5; 5; 4; 2; 6; 3; 0; 5; 5; 1; 4; 3; 4; 3; 4; 4; 2; 1; 5; 2; 5; 5; 2; 8; 5; 3; 4; 3; 2; 4. Проверьте гипотезу о том, что данная выборка имеет распределение Пуассона. Уровень значимости a = 0,05. Объем выборки n = 160. 126. 5; 2; 5; 5; 3; 4; 1; 4; 4; 1; 1; 3; 1; 3; 2; 4; 1; 5; 2; 1; 2; 2; 3; 2; 1; 2; 1; 4; 1; 2; 5; 5; 1; 5; 4; 2; 2; 4; 4; 2; 4; 2; 5; 4; 1; 5; 5; 4; 5; 1; 4; 3; 2; 4; 1; 5; 4; 3; 1; 1; 4; 2; 4; 5; 4; 4; 5; 5; 1; 4; 4; 2; 5; 3; 4; 1; 5; 3; 2; 3; 4; 4; 5; 1; 5; 4; 5; 1; 4; 5; 1; 5; 2; 3; 5; 1; 2; 2; 2; 5; 5; 4; 1; 5; 4; 5; 2; 3; 1; 5; 2; 3; 5; 2; 5; 1; 4; 4; 2; 4. Проверьте гипотезу о равномерном дискретном распределении рассматриваемой величины по данной выборке. Уровень значимости a = 0,05. Объем выборки n = 120. 127. 3; 4; 3; 4; 3; 4; 3; 5; 1; 4; 5; 5; 2; 4; 1; 4; 3; 2; 2; 4; 3; 3; 4; 5; 4; 1; 4; 4; 3; 3; 5; 5; 5; 4; 3; 3; 5; 2; 2; 4; 4; 2; 3; 4; 3; 3; 3; 2; 4; 2; 3; 4; 4; 4; 4; 4; 4; 4; 4; 4; 7; 4; 3; 5; 3; 4; 2; 4; 4; 4; 5; 3; 6; 5; 5; 5; 5; 4; 3; 3; 4; 4; 4; 4; 5; 4; 3; 5; 4; 4; 4; 5; 2; 4; 2; 4; 3; 2; 5; 4; 3; 1; 5; 3; 2; 5; 4; 2; 5; 6; 3; 4; 2; 2; 3; 3; 2; 4; 6; 3; 4; 2; 4; 3; 5; 5; 4; 2; 3; 4; 2; 3; 2; 4; 4; 2; 2; 4; 5; 4. Проверьте гипотезу о биномиальном распределении рассматриваемой величины по данной выборке. Уровень значимости a = 0,1. Объем выборки n = 140. 128. 4; 1; 3; 4; 3; 1; 0; 1; 1; 3; 1; 0; 0; 2; 4; 5; 3; 0; 2; 4; 0; 4; 0; 3; 1; 2; 4; 0; 3; 1; 3; 3; 3; 1; 2; 5; 1; 0; 3; 0; 1; 1; 1; 2; 2; 2; 1; 2; 2; 4; 6; 1; 4; 8; 4; 1; 3; 2; 1; 1; 0; 4; 3; 2; 3; 3; 3; 5; 1; 2; 4; 4; 0; 5; 1; 1; 2; 1; 0; 3; 1; 3; 4; 2; 4; 1; 1; 1; 1; 2; 0; 3; 4; 3; 2; 1; 4; 2; 3; 1; 1; 2; 3; 2; 2; 1; 4; 5; 3; 2; 3; 0; 2; 4; 1; 4; 1; 1; 0; 3; 2; 1; 2; 1; 4; 3; 0; 2; 4; 1; 2; 5; 4; 1; 0; 3; 1; 2; 3; 3; 4; 1; 3; 7; 1; 6; 3; 3; 2; 3; 0; 5; 2; 2; 2; 3; 4; 1; 1; 0; 3; 1; 2; 0; 2; 3; 6; 1; 1; 3; 2; 1; 3; 2; 2; 3; 1; 3; 3; 3. Проверьте гипотезу о том, что данная выборка имеет распределение Пуассона. Уровень значимости a = 0,05. Объем выборки n = 180. 129. 5; 6; 8; 2; 4; 6; 2; 2; 1; 2; 3; 5; 7; 8; 6; 6; 4; 7; 7; 3; 7; 8; 4; 1; 7; 4; 1; 6; 5; 2; 5; 7; 8; 4; 5; 7; 7; 7; 2; 8; 7; 1; 6; 8; 3; 3; 6; 5; 5; 6; 4; 7; 3; 5; 3; 8; 7; 7; 6; 1; 3; 6; 8; 5; 1; 6; 7; 8; 1; 2; 7; 4; 8; 5; 4; 7; 8; 6; 3; 7; 3; 4; 8; 8; 8; 7; 5; 6; 3; 6; 6; 6; 2; 5; 1; 5; 5; 4; 7; 5; 6; 1; 8; 3; 6; 5; 5; 5; 7; 3; 4; 2; 3; 2; 5; 4; 1; 7; 6; 5; 8; 8; 4; 8; 2; 5; 3; 3; 4; 3; 8; 2; 1; 8; 6; 5; 3; 8; 3; 3; 3; 4; 8; 2; 2; 6; 6; 8; 4; 7; 2; 7; 1; 1; 1; 1; 4; 6; 2; 8; 1; 4; 4; 5; 8; 6; 2; 8; 3; 8; 1; 3; 3; 3; 3; 6; 6; 5; 6; 8; 6; 5; 3; 1; 6; 4; 1; 6; 7; 8; 3; 6; 8; 2; 4; 1; 6; 8; 8; 7.
Проверьте гипотезу о равномерном дискретном распределении рассматриваемой величины по данной выборке. Уровень значимости a = 0,05. Объем выборки n = 200. 130. 1; 3; 2; 3; 2; 3; 4; 0; 1; 3; 0; 2; 2; 6; 0; 3; 2; 3; 1; 1; 2; 2; 2; 2; 0; 8; 3; 3; 5; 0; 3; 3; 0; 2; 1; 1; 1; 2; 1; 0; 3; 0; 3; 1; 2; 0; 2; 2; 3; 2; 3; 2; 3; 3; 2; 2; 4; 1; 2; 1; 3; 2; 3; 4; 3; 0; 4; 2; 2; 6; 4; 2; 1; 2; 3; 4; 1; 1; 1; 5; 2; 1; 3; 4; 1; 3; 4; 1; 2; 2; 2; 0; 1; 1; 2; 3; 3; 5; 1; 2; 2; 3; 3; 5; 2; 4; 2; 4; 0; 5; 3; 1; 0; 3; 2; 3; 2; 4; 4; 3; 3; 4; 2; 4; 3; 0; 0; 1; 3; 1; 1; 1; 0; 1; 5; 2; 0; 3; 3; 4; 3; 3; 4; 3; 1; 5; 1; 1; 3; 0; 1; 1; 1; 1; 3; 2; 0; 3; 2; 5; 1; 3; 2; 1; 1; 0; 2; 1; 0; 2; 1; 4; 5; 4; 1; 0; 1; 4; 2; 2; 2; 0; 2; 4; 1; 2; 1; 0; 1; 2; 4; 1; 3; 1; 5; 2; 3; 1; 8; 1. Проверьте гипотезу о том, что данная выборка имеет распределение Пуассона. Уровень значимости a = 0,05. Объем выборки n = 200. Примеры выполнения заданий 12 1-13 0 Пример 1. На массовых соревнованиях спортсмены-стрелки производят по 6 выстрелов. Ниже приведены их результаты (количество попаданий по мишени): 6; 6; 3; 5; 4; 6; 6; 6; 6; 5; 6; 6; 4; 6; 4; 6; 5; 3; 4; 5; 3; 6; 4; 6; 6; 3; 4; 4; 5; 3; 4; 3; 4; 5; 4; 5; 6; 5; 5; 6; 5; 5; 6; 6; 6; 6; 5; 5; 6; 6; 4; 5; 5; 6; 6; 4; 5; 6; 6; 5; 4; 4; 4; 2; 4; 5; 4; 3; 4; 4; 5; 4; 5; 5; 5; 6; 6; 6; 4; 5; 4; 3; 5; 5; 6; 6; 4; 6; 4; 6; 5; 4; 5; 4; 5; 5; 4; 6; 5; 4; 4; 4; 5; 6; 5; 5; 2; 5; 6; 3; 6; 5; 4; 5; 6; 6; 4; 3; 5; 5; 4; 3; 2; 4; 4; 5; 5; 6; 5; 6; 6; 6; 5; 4; 6; 5; 4; 5; 5; 3; 5; 4; 6; 5; 5; 4; 4; 1; 6; 6; 5; 5; 4; 5; 5; 6; 3; 6; 6; 4. Проверьте гипотезу о биномиальном распределении количества попаданий по данной выборке. Уровень значимости a = 0,05. Решение. Данная случайная величина (количество попаданий) принимает значения от 1 до 6. Находим абсолютные частоты для всех этих значений (подсчитываем, сколько стрелков имеют 1, 2, 3, 4, 5 и 6 попаданий в мишень). Заносим данные в таблицу 3. Рассчитываем по формуле Таблица 11
После этого вычисляем среднее выборочное числа попаданий:
Определяем выборочную дисперсию и выборочное среднее квадратическое отклонение:
Теперь проверим гипотезу о том, что распределение числа попаданий является биномиальным: H 0: распределение числа попаданий является биномиальным; H 1: распределение числа попаданий не является биномиальным. Прежде всего, объединяем два первых интервала, добавив туда же значение числа попаданий, равное 0 (см. таблицу 10), т.к. их эмпирические частоты mi меньше 4. Данные заносим в таблицу 11 (столбец mi). Считаем, что данное распределение является биномиальным с математическим ожиданием 4,80. Т.к. при биномиальном распределении M (X) = np, то вероятность попадания при одном выстреле будет равна
Умножаем эти вероятности на объём выборки (n = 160) и получаем теоретические частоты (mi ’). Заполняем два оставшихся столбца и находим суммы по столбцам. Таблица 12
Последняя сумма соответствует искомому критерию
Данная выборка разбита на l = 7 интервалов. В биномиальном распределении р = 1 подбираемых параметра (вероятность появления события при одном испытании). Поэтому число степеней свободы в данном случае k = l - p - 1 = 7 - 1 - 1 = 5. При уровне значимости a = 0,05 и найденному числу степеней свободы из таблицы критических точек распределения c 2 находим значение критерия Т.к. Пример 2. В учётном журнале фиксируются вызовы ремонтной бригады. Студент-практикант построил вариационный ряд количества вызовов за смену:
Проверьте гипотезу о том, что количества вызовов за смену имеют распределение Пуассона. Уровень значимости a = 0,1. Решение. Вычисляем среднее выборочное числа вызовов:
H 0: число вызовов имеют распределение Пуассона; H 1: число вызовов не имеют распределение Пуассона. Прежде всего, объединяем последние интервалы, т.к. их эмпирические частоты mi меньше 4. Данные заносим в таблицу 10 (столбец mi). Считаем, что данное распределение является пуассоновским с математическим ожиданием 2,46. Тогда по формуле Пуассона находим вероятности нужного числа вызовов:
Тогда вероятность того, что будет более 5 вызовов равна P (>5) = 1 – (P (0) + P (1) + P (2) + P (3) + P (4) + P (5)) = = 1 – (0,0854 + 0,2102 + 0,2585 + 0,2120 + 0,1304 + 0,0641) = 0,0394. Умножаем эти вероятности на объём выборки (n = 160) и получаем теоретические частоты (mi ’). Заполняем два оставшихся столбца и находим суммы по столбцам. Таблица 13
Последняя сумма соответствует искомому критерию Данная выборка разбита на l = 7 интервалов. В распределении Пуассона р = 1 подбираемых параметра (математическое ожидание). Поэтому число степеней свободы в данном случае k = l - p - 1 = 7 - 1 - 1 = 5. При уровне значимости a = 0,1 и найденному числу степеней свободы из таблицы критических точек распределения c 2 находим значение критерия Т.к. Пример 3. Для статистического анализа некоторой случайной величины был построен вариационный ряд:
Проверьте гипотезу о том, что данная случайная величина имеет равномерное дискретное распределение. Уровень значимости a = 0,1. Решение. Выдвигаем основную и альтернативную гипотезы: H 0: данная случайная величина имеет равномерное дискретное распределение; H 1: данная случайная величина не имеет равномерное дискретное распределение. Считаем, что данное распределение является равномерным дискретным. Тогда вероятности всех значений этой величины одинаковы и равны Заполняем два оставшихся столбца и находим суммы по столбцам. Таблица 14
Последняя сумма соответствует искомому критерию Данная выборка разбита на l =7 интервалов. Для дискретного равномерного распределения р = 0 (подбираемых параметра нет). Поэтому число степеней свободы в данном случае k = l - p - 1 = 7 - 0 - 1 = 6. При уровне значимости a = 0,1 и найденному числу степеней свободы из таблицы критических точек распределения c 2 находим значение критерия Т.к.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 93; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.136.235 (0.063 с.) |
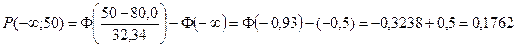 ;
;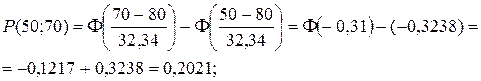
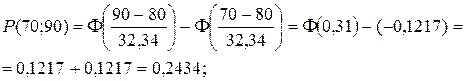

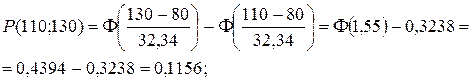
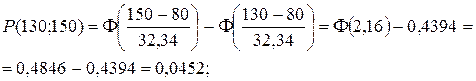
 .
.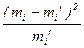
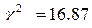 .
.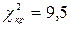 (смотрите в приложениях).
(смотрите в приложениях).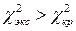 , то нулевая гипотеза отвергается: распределение не является нормальным.
, то нулевая гипотеза отвергается: распределение не является нормальным.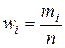 значения относительных частот и по формуле
значения относительных частот и по формуле 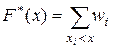 значения эмпирической функции распределения (накопленные частоты).
значения эмпирической функции распределения (накопленные частоты).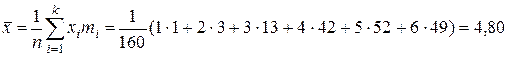 .
.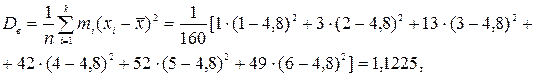
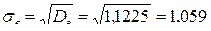 .
.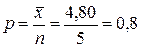 . Тогда по формуле Бернулли находим вероятности 0, 1, 2, 3, 4, 5 и 6 попаданий:
. Тогда по формуле Бернулли находим вероятности 0, 1, 2, 3, 4, 5 и 6 попаданий: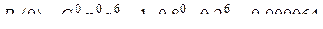 ;
;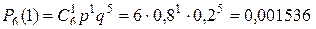 ;
; ;
;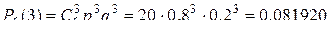 ;
;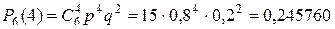 ;
;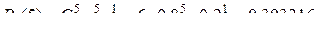 ;
;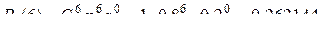 .
.
 .
.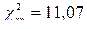 .
.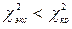 , то нулевая гипотеза принимается: выборочные данные не противоречат тому, что распределение числа попаданий является биномиальным.
, то нулевая гипотеза принимается: выборочные данные не противоречат тому, что распределение числа попаданий является биномиальным.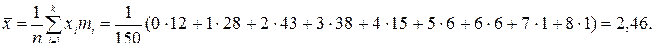 После этого проверим гипотезу о том, что количества вызовов за смену имеют распределение Пуассона:
После этого проверим гипотезу о том, что количества вызовов за смену имеют распределение Пуассона: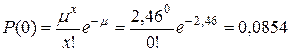 ;
; 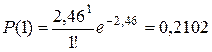 ;
;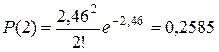 ;
; 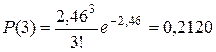 ;
;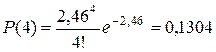 ;
; 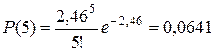 .
.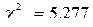 .
.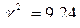 .
. (k – количество значений случайной величины). Умножаем эту вероятности на объём выборки (n = 180) и получаем теоретические частоты mi ’ = 0,1429×180 = 25,714 (они также будут все одинаковыми).
(k – количество значений случайной величины). Умножаем эту вероятности на объём выборки (n = 180) и получаем теоретические частоты mi ’ = 0,1429×180 = 25,714 (они также будут все одинаковыми).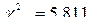 .
. (Приложение 3).
(Приложение 3).


