
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики случайных величин
Законы распределения полностью описывают случайные величины и с их помощью можно рассмотреть характеристики положения случайной величины и характеристики рассеивания случайной величины. Математическое ожидание случайной величины – характеристика среднего ожидаемого значения случайной величины. Математическое ожидание дискретной случайной величины с рядом распределения при
При введении числа опытов N по наблюдению за дискретной случайной величины, тогда среднее арифметическое для случайной величины определяется соотношением
Для непрерывной случайной величины с плотностью распределения
Мода случайной величины – наиболее вероятное значение этой случайной величины. Для дискретной случайной величины мода равна тому значению Если у многоугольника или у графика плотности распределения несколько выраженных максимумов, тогда распределение называется полимодальным. Для одномодального распределения с симметричным графиком мода и математическое ожидание совпадают. Медиана для непрерывной случайной величины – число
Дисперсия случайной величины – математическое ожидание квадрата отклонения этой случайной величины от математического ожидания
Для дискретной случайной величины дисперсия определяется соотношением
Для непрерывной случайной величины дисперсия определяется соотношением
Теорема: Среднеквадратическое отклонение случайной величины – число, определяемое соотношением
Если в одном опыте наблюдаются сразу несколько случайных величин, тогда можно ставить вопрос об их зависимости или независимости. Две случайные величины X и Y называются независимыми, если закон распределения каждой не зависит от того, какое значение приняла вторая случайная величина. Свойства математического ожидания и дисперсии случайной величины: 1. 2. 3.
4. 5. 6. Для биноминального распределения при
Случайная величина X, принимающая значения 0, 1, 2, …, m, … с вероятностями равными
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 68; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.107 (0.006 с.) |
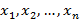 :
: 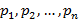 – число, определяемое соотношением
– число, определяемое соотношением

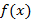 математическое ожидание определяется соотношением
математическое ожидание определяется соотношением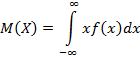
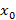 , у которого наибольшая частота повторений в ряде распределения. Для непрерывной случайной величины мода – точка максимума функции плотности распределения.
, у которого наибольшая частота повторений в ряде распределения. Для непрерывной случайной величины мода – точка максимума функции плотности распределения. , для которого выполняется следующее соотношение
, для которого выполняется следующее соотношение
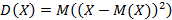
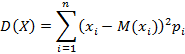
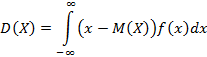
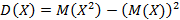 .
.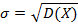
 ;
;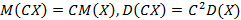 ;
; для независимых случайных величин;
для независимых случайных величин;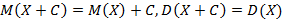 ;
; ;
;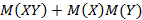 для независимых случайных величин,
для независимых случайных величин, 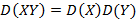 для независимых случайных величин и их математические ожидания равны нулю.
для независимых случайных величин и их математические ожидания равны нулю.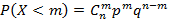 математическое ожидание и дисперсия примут вид
математическое ожидание и дисперсия примут вид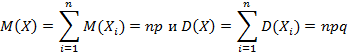
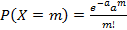 , где
, где 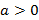 , называется распределением Пуассона. Если случайная распределена по закону Пуассона, тогда
, называется распределением Пуассона. Если случайная распределена по закону Пуассона, тогда  и
и 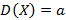 . Распределение Пуассона является предельным для биномиального при бесконечном количестве опытов и
. Распределение Пуассона является предельным для биномиального при бесконечном количестве опытов и 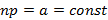 .
.


