
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интеграл от функции комплексной переменной
Пусть задана некоторая область D и в этой области задана непрерывная в заданной области функция
Разделив кривую на n произвольных частей, получим семейство дуг вида
Исходя из этого получим следующее соотношение
Свойства интеграла комплексной переменной 1. Интеграл от алгебраической суммы равен алгебраической сумме интегралов. Справедливо для любого конечного числа слагаемых; 2. 3. 4. 5. 6. Вычислить интеграл от комплексной переменной можно следующим образом
Полученное соотношение – контурный интеграл второго рода. Контурный интеграл первого рода, где
Интегральная теорема Коши для некоторой области Если функция
В условиях многосвязной области, которая может возникать в случае, когда функция комплексной переменной не аналогична в некоторой точке или области, ограниченной контуром
Исходя из этого соотношения получим для соотношение двусвязной области вида
Интегральная формула Коши Пусть задана функция
Доопределение
Из данного соотношения следует интегральная формула Коши
Следствия интегральной формулы Коши для производных аналитических функций примут следующие виды
Из полученного соотношения следует соотношение интегральной формулы коши для производных высших порядков аналитических функций
Для справедливости полученных соотношений, необходимо, чтобы функции удовлетворяли условиям коши – функции должны быть аналитичны в рассматриваемой области и на заданном контуре.
Теория рядов Числовые ряды Числовым рядом называется бесконечная сумма вида
Если существует конечный предел частичной суммы, тогда ряд называется сходящимся, а число S – сумма ряда
Если предел не существует или равен бесконечности, тогда ряд называется расходящимся. Ряд вида
Исходя из известного со школы соотношения для суммы геометрической прогрессии, следует следующие соотношение
При особых случаях, когда
Геометрическая прогрессия сходится при
Операции с рядами Если Если ряд При удалении или добавлении конечного числа слагаемых поведения ряда не меняется. Необходимый признак сходимости – предел вида
Знакоположительные ряды Знакоположительным рядом называется ряд вида
Теорема 1 – Признак сравнения: Пусть для знакоположительных рядов Теорема 2 - Предельный признак: Если для знакоположительных рядов Теорема 3 – Признак Даламбера: Пусть для знакоположительного ряда Теорема 4 – Признак Коши: Пусть для знакоположительного ряда
Теорема 5 – Интегральный признак Коши: Пусть для знакоположительного ряда
|
||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.213.128 (0.01 с.) |
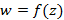 и некоторая кусочно-гладкая кривая
и некоторая кусочно-гладкая кривая 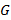
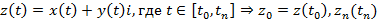
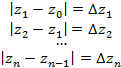
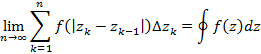
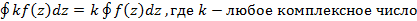 ;
;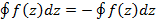 ;
;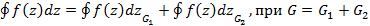
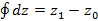 ;
;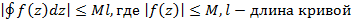 ;
;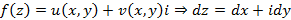
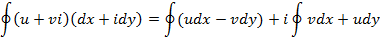
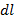 – дифференциал длины дуги имеет вид
– дифференциал длины дуги имеет вид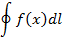
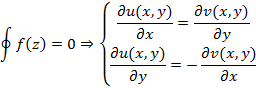
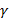 , интегральная теорема Коши представляется в виде суммы интегралов, рассматриваемых при односвязных областях
, интегральная теорема Коши представляется в виде суммы интегралов, рассматриваемых при односвязных областях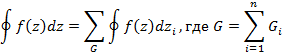
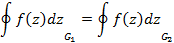
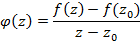
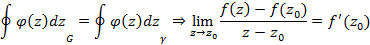
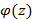 в точке
в точке 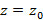 как производную заданной функции в этой точке требует непрерывности функции в этой точке, из которого следует соотношение – интеграл Коши
как производную заданной функции в этой точке требует непрерывности функции в этой точке, из которого следует соотношение – интеграл Коши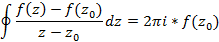
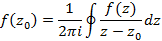
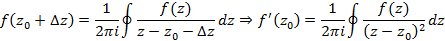
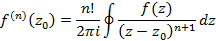
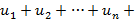 , где
, где 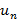 – общий член ряда. Сумма первых n членов ряда называется частичной суммой
– общий член ряда. Сумма первых n членов ряда называется частичной суммой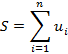
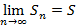
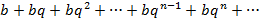 называется геометрической прогрессией, где b – первый член ряда, q – знаменатель прогрессии
называется геометрической прогрессией, где b – первый член ряда, q – знаменатель прогрессии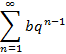
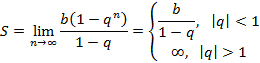
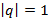 , получим расходящиеся ряды следующих видов с соответствующими суммами
, получим расходящиеся ряды следующих видов с соответствующими суммами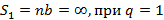
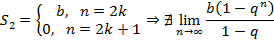
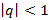 и расходится во всех остальных случаях.
и расходится во всех остальных случаях.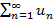 и
и 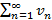 – сходящиеся ряды с суммами
– сходящиеся ряды с суммами 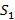 и
и 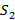 соответственно, тогда ряд
соответственно, тогда ряд 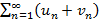 также сходится и его сумма равна
также сходится и его сумма равна 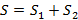 .
.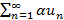 также сходится и его сумма равна
также сходится и его сумма равна 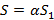 .
.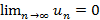 не является достаточным. Например, гармонический рад вида
не является достаточным. Например, гармонический рад вида 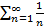 имеет необходимый предел, но является расходящимся рядом.
имеет необходимый предел, но является расходящимся рядом.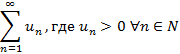
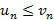 , тогда справедливо следующее: из сходимости большего следует сходимость меньшего или из расходимости меньшего следует расходимость большего.
, тогда справедливо следующее: из сходимости большего следует сходимость меньшего или из расходимости меньшего следует расходимость большего.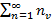 существует конечный предел вида
существует конечный предел вида 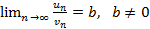 , тогда ряды ведут себя одинаково: оба сходятся или оба расходятся.
, тогда ряды ведут себя одинаково: оба сходятся или оба расходятся.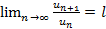 , тогда если
, тогда если 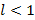 – ряд сходится,
– ряд сходится, 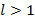 – ряд расходится,
– ряд расходится, 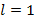 – признак не работает.
– признак не работает.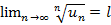 , тогда если
, тогда если 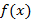 , определенная на отрезке
, определенная на отрезке 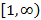 со свойствами:
со свойствами: 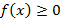 ,
, 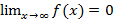 ,
, 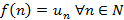 . Тогда ряд и несобственный интеграл
. Тогда ряд и несобственный интеграл 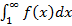 ведут себя одинаково: оба сходятся или оба расходятся.
ведут себя одинаково: оба сходятся или оба расходятся.


