Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знакопеременные и знакочередующиеся ряды
Ряд Ряды вида Теорема – Признак Лейбница: Если для модулей членов знакочередующегося ряда выполняются следующие условия: Если у знакопеременного ряда сходится ряд из модулей, тогда сам исходный ряд также сходится (обратное высказывание неверно). Если у сходящегося знакопеременного ряда ряд из модулей сходится, тогда исходный ряд называется абсолютно сходящимся. Если ряд из модулей расходится – условно сходящимся. Если ряд сходится абсолютно, тогда перестановка бесконечного числа слагаемых не влияет на сумму. Перестановка слагаемых у условно сходящегося ряда может привести к любому значению суммы или привести к расходимости ряда.
Функциональные ряды Бесконечная сумма вида Множество всех значений x, при которых функциональный ряд сходится называется областью сходимости ряда. Аналогично числовым рядам можно ввести частичные суммы следующего вида
Если x принадлежит области сходимости, тогда сумма ряда
Степенные ряды Функциональный ряд называется степенным, если элементы ряда определены степенной функцией
Частный случай при
У степенного ряда вида
На концах интервала сходимости ряд может быть сходящимся, так и расходящимся. Если степенной ряд сходится на своем интервале сходимости к функции суммы ряда 1. 2. Ряд можно почленно дифференцировать
3. Ряд можно почленно интегрировать
Полученные ряды также имеют интервал сходимости.
Ряды Тейлора и Маклорена
Если функция
называется рядом Тейлора для функции Достаточное условие представимости функции рядом Тейлора следующее: если в окрестности Ряд Тейлора при
называется рядом Маклорена. Разложение в ряд Маклорена некоторых функций
Основным практическим приложением рядом Маклорена является вычисление определенных интегралов с некоторой точностью, для чего подынтегральная функция раскладывается в ряд Маклорена и полученный ряд интегрируется почленно.
Ряды в комплексной области Вся теория рядов в комплексной области сводится к поэлементному рассмотрению
Функциональный ряд в комплексной области вида
Сходится на области D, если в каждой точке заданной области ряд сходится. Если справедливо соотношение Если члены заданного ряда в комплексной области непрерывны в области D и заданный ряд равномерно сходится, тогда сумма ряда
Если члены заданного ряда в комплексной области аналитичны в некоторой области D и ряд сходится в области D равномерно, тогда дифференциал суммы ряда примет вид
Ряд дифференциалов элементов ряда сводится к дифференциалу суммы ряда равномерно.
|
|||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.120.109 (0.009 с.) |
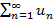 , у которого присутствуют и положительные и отрицательные слагаемые называется знакопеременным.
, у которого присутствуют и положительные и отрицательные слагаемые называется знакопеременным.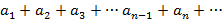 , где
, где 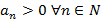 называется знакочередующимся.
называется знакочередующимся.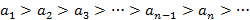 и
и 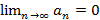 , тогда ряд сходится и его сумма по модулю оценивается как
, тогда ряд сходится и его сумма по модулю оценивается как 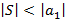 .
.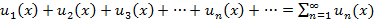 называется функциональным рядом. Если у функционального ряда зафиксировать точку
называется функциональным рядом. Если у функционального ряда зафиксировать точку 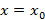 , тогда ряд станет числовым.
, тогда ряд станет числовым.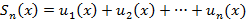
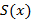 определена на области сходимости ряда
определена на области сходимости ряда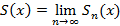
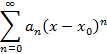
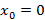 , тогда степенной ряд примет вид
, тогда степенной ряд примет вид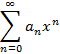
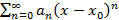 всегда существует число R со следующим свойством: ряд сходится на интервале
всегда существует число R со следующим свойством: ряд сходится на интервале 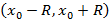 и расходится на лучах
и расходится на лучах 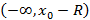 и
и 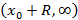 . Число R называется радиусом сходимости, а интервал
. Число R называется радиусом сходимости, а интервал 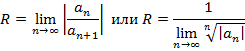
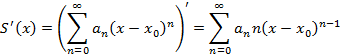
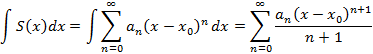
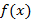 дифференцируема в окрестности точки
дифференцируема в окрестности точки 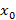 бесконечное число раз, тогда степенной ряд следующего вида
бесконечное число раз, тогда степенной ряд следующего вида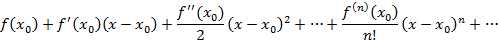
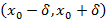 функция
функция 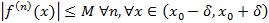 , иными словами ряд Тейлора в этой окрестности сходится к
, иными словами ряд Тейлора в этой окрестности сходится к 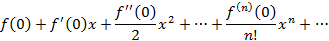
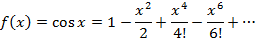
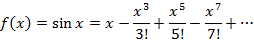
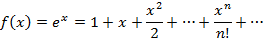
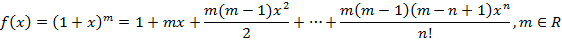
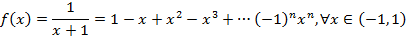
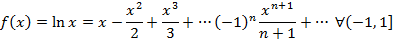
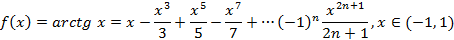
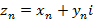 , из чего следует, что рассматриваются два ряда: действительный и мнимый, при этом, если расходится хотя бы один из них, тогда весь ряд расходится
, из чего следует, что рассматриваются два ряда: действительный и мнимый, при этом, если расходится хотя бы один из них, тогда весь ряд расходится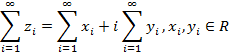
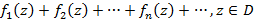
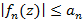 , тогда ряд сходится в области D равномерно – признак равномерной сходимости Вейерштрассе.
, тогда ряд сходится в области D равномерно – признак равномерной сходимости Вейерштрассе.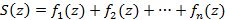 также непрерывна в области D. При тех же условиях справедливо также следующее соотношение
также непрерывна в области D. При тех же условиях справедливо также следующее соотношение