
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события. Типы событий. Пространство элементарных событий
Опытом называется комплекс условий и действий, которые можно повторить неограниченное число раз. Случайным событием называется такое событие, которое связанно с данным опытом и про которое по исходу опыта можно точно сказать произошло оно или нет. Если результат некоторого опыта происходит один из взаимоисключающих друг друга исходов, тогда эти исходы называют элементарными событиями. Множество всех элементарных событий называют пространством элементарных событий – ПЭС. ПЭС можно вводить разными способами, которые зависят от классификации. События разделяются на следующие типы: достоверное событие – событие, которое обязательно произойдет в данном опыте и невозможное событие – событие, которое никогда не произойдет в данном опыте. Помимо данной классификации события могут быть: несовместными – события не могут произойти в одном опыте и совместными – события могут произойти в одном опыте. Событие A благоприятствует событию B, если из того, что произошло событие A автоматически вытекает, что произошло событие B
Полная группа несовместных событий (ПГНС) – множество событий, которые могут произойти в результате данного опыта, удовлетворяющие условиям 1. Все события попарно несовместные; 2. В сумме все события образуют ПЭС. Пространство элементарных событий всегда является полной группой несовместных событий. Рассмотрим опыт, удовлетворяющий двум условиям: число возможных исходов или элементарных событий конечно и равно n и все исходы равновероятны – классическая схема. Пусть случайной событие A, тогда
Поскольку
Элементы комбинаторики Пусть даны два множества
Пусть существует множество из n элементов и n упорядоченных ячеек. Каждое заполнение ячеек – перестановок равно соотношению
Есть множество из n элементов и m упорядоченных ячеек
Есть множество из n элементов и одна ячейка на m мест без упорядочивания. Каждое заполнение – сочетание равно соотношению
Геометрическая вероятность Пусть
В данном соотношении мера – длина, площадь или объем. Рассматриваемое соотношение называется геометрической вероятностью. У геометрической вероятности справедливы следующие свойства: 1. 2. Если A – невозможно, тогда A как множество пусто, тогда 3. Если A – достоверное, тогда
Статистическая вероятность Пусть известно, что событие A имеет вероятность P. При проведении n опытов и фиксации количества наступления события A, тогда число Исходя из теоремы Бернулли Пусть в серии из n независимых опытов нас интересует событие A в каждом опыте. Если оно произошло в конкретном опыте, тогда этот исход опыта – успешный и пусть p – вероятность успеха, соответственно
Данное соотношение – схема Бернулли. При необходимости найти вероятность
Свойства вероятности Если A и B – совместные события, тогда
Если рассматриваемые n событий и в сумме они дают полную группу несовместных событий, тогда сумма их вероятностей равна единице. Вероятностью A при условии B
Событие A называется независимым от события B, если Пусть
Данное соотношение определяется формулой Байеса
Случайные величины Случайные величины – числовые величины, которые могут принимать в результате опыта то или иное значения, причем заранее не известно какое именно. Если все возможные значения случайной величины можно пронумеровать, тогда ее называют дискретной случайной величиной. Непрерывной случайной величиной называют случайные величины, которые занимают конечный или непрерывный промежуток целиком. Любое правило, которое позволяет находить вероятность того, что случайная величина примет заданное значение или попадает в заданный промежуток значений называется законом распределения. Пусть X принимает значения Случайная величина, которая принимает значения Если n в схеме Бернулли большое, тогда вычисления становятся очень громоздкими, поэтому при определении условных вероятностей можно воспользоваться приближенными формулами, такими как формула Пуассона
Для непрерывной случайной величины невозможно построить ряд распределения и вероятность принять конкретное значение равно нулю. Исходя из этого, целесообразно рассматривать вероятность вида Функцией распределения случайной величины X называется функция следующего вида
Сроить функцию распределения можно как для непрерывных случайных величин, так и для дискретных случайных величин В случае дискретного ряда распределения, функция распределения примет ступенчатый вид. Если
Свойства функции плотности распределения: 1. 2. 3. 4. Исходя из указанных свойств, следует, что на всем интервале
|
|||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 60; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.126 (0.013 с.) |

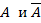 всегда являются полной группой несовместных событий.
всегда являются полной группой несовместных событий.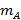 – число элементарных событий, благоприятствующих A, тогда вероятность события A удовлетворяет соотношению
– число элементарных событий, благоприятствующих A, тогда вероятность события A удовлетворяет соотношению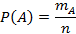
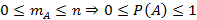 , тогда при
, тогда при 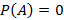 – событие A невозможно или
– событие A невозможно или 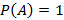 – событие A достоверное.
– событие A достоверное.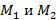 из
из 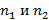 элементов соответственно. Число способов образовать пару таким образом, чтобы один элемент был из одного множества, а второй из второго, равно
элементов соответственно. Число способов образовать пару таким образом, чтобы один элемент был из одного множества, а второй из второго, равно  . Аналогично для трех элементов из множеств, число способов образовать тройку элементов равно
. Аналогично для трех элементов из множеств, число способов образовать тройку элементов равно 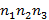 . Если имеется m множеств из
. Если имеется m множеств из 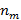 элементов, тогда существует
элементов, тогда существует 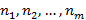 способов построить набор из m элементов.
способов построить набор из m элементов.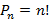
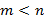 . Каждое заполнение ячеек – размещение равно соотношению
. Каждое заполнение ячеек – размещение равно соотношению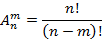

 – некоторая область на прямой, плоскости или в пространстве; A – часть
– некоторая область на прямой, плоскости или в пространстве; A – часть 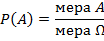
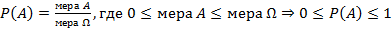 ;
;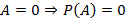 ;
; называют относительной частотой A в этих n опытов – статистический подход.
называют относительной частотой A в этих n опытов – статистический подход.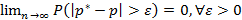 следует, что относительная частота
следует, что относительная частота  ведет себя устойчиво, иными словами, она колеблется около P и с увеличением числа опытов n эти колебания затухают. Исходя из этого, если P не известно, тогда берут
ведет себя устойчиво, иными словами, она колеблется около P и с увеличением числа опытов n эти колебания затухают. Исходя из этого, если P не известно, тогда берут 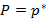 , при большом n – статистическая вероятность.
, при большом n – статистическая вероятность. – вероятность неудачи. Исходя из всего выше сказанного, следует, что вероятность
– вероятность неудачи. Исходя из всего выше сказанного, следует, что вероятность 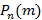 того, что в серии из n опытов ровно m успехов равно соотношению
того, что в серии из n опытов ровно m успехов равно соотношению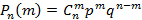
 , тогда можно воспользоваться суммой несовместных событий
, тогда можно воспользоваться суммой несовместных событий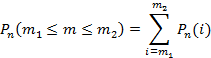
 – теорема сложения вероятностей. При условии A и B – несовместные события, тогда справедливо следующее
– теорема сложения вероятностей. При условии A и B – несовместные события, тогда справедливо следующее 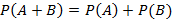 – следствие теоремы сложения вероятностей при
– следствие теоремы сложения вероятностей при  . Если
. Если  – попарно несовместные, тогда справедливо следующе соотношение
– попарно несовместные, тогда справедливо следующе соотношение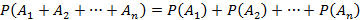
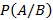 называется вероятностью события A при условии, что событие B точно произошло. Если событие B произошло, тогда пространство элементарных событий сужается до B при этом от A остается часть равная AB, тогда справедливо следующее соотношение, определяющее условную вероятность
называется вероятностью события A при условии, что событие B точно произошло. Если событие B произошло, тогда пространство элементарных событий сужается до B при этом от A остается часть равная AB, тогда справедливо следующее соотношение, определяющее условную вероятность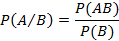
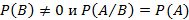 , иными словами, наступление или отсутствие события B не влияет на событие A.
, иными словами, наступление или отсутствие события B не влияет на событие A.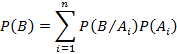
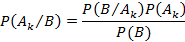
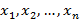 с вероятностями
с вероятностями 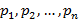 соответственно, тогда таблица типа значение-вероятность называется рядом распределения дискретной случайной величины. Графическое изображение данного ряда распределения – многоугольник распределения.
соответственно, тогда таблица типа значение-вероятность называется рядом распределения дискретной случайной величины. Графическое изображение данного ряда распределения – многоугольник распределения. с вероятностями равными
с вероятностями равными 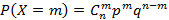 , где p – некоторое число из отрезка
, где p – некоторое число из отрезка 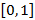 ;
; 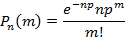
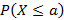 или
или 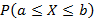 .
.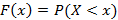 со свойствами:
со свойствами: 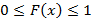 ,
, 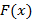 – не убывает,
– не убывает, 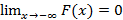 и
и 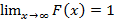 . Для любой непрерывной случайной величины справедливо следующие определения вероятности в случае нахождения значения на отрезке или на луче с известным началом
. Для любой непрерывной случайной величины справедливо следующие определения вероятности в случае нахождения значения на отрезке или на луче с известным началом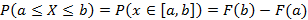
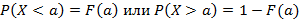
 – функция плотности распределения непрерывной случайной величины.
– функция плотности распределения непрерывной случайной величины.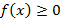 ;
;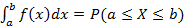 ;
;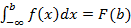 ;
; .
.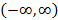 функция плотности распределения стремится к нулю.
функция плотности распределения стремится к нулю.


