
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимизация логических функций
Ранее показано, что любую логическую функцию можно представить с применением только основных булевых функций. Ее СДНФ и СКНФ находятся однозначно, но обычно содержат избыточное число элементов. Существуют ДНФ и КНФ с такими же значениями функции, но с меньшим числом элементов. Они более удобны для составления переключательной схемы и для изображения логическими элементами по ГОСТ и ANSI. В большинстве случаев для булевых функций имеется несколько различных представлений как ДНФ, так и КНФ. Для функции Индексом простоты или сложности булевой функции 1. Не отрицательность – для любой ДНФ обозначением R выполнено 2. Монотонность - 3. Выпуклость - 4. Инвариантность – при получении Виды индексов сложности: Обычно к сокращенной ДНФ переходят из ДНФ операциями поглощения и склеивания. Логическое произведение любого числа аргументов является элементарным преобразованием, если множители являются либо одиночные элементы, либо их отрицания. Законы поглощения имеют вид
Законы склеивания имеют вид
Перечисленные законы применяются для получения сокращённой ДНФ и скрещённой КНФ. Еще одним способом минимизации логических функций является применение карт Карно и Вейна. Данные карты содержат
Рисунок 66. Минимизация логической функции с помощью карт Карно.
Из таблицы истинности или подстановкой каждого набора из значений переменных подставляя значения функции получим карту Вейча. Если в двух соседних клетках одинаковое значение логической функции Способ минимизации логической функции на двоичном кубе размерности n подразумевает построение его с вершинами – наборами значений переменных и заполнением значениями функции. При наличии ребра между вершинами, можно по закону склейки получить один дизъюнкт ранга 1. Обычно двоичный куб проецируется на плоскость. В общем случае при наличии ребра при Метод минимизации Квайна-Макласске подразумевает выполнение указанных последовательных действий 1. Для логической функции 2. Составляется сокращенная ДНФ или сокращенная КНФ; 3. Составляется набор имплекантов, по которому составляется базисный набор – одна из комбинаций минимальной ДНФ – МДНФ. Для логической функции 1. Если при некотором значении имплекант 2. Исключение хотя бы одного множителя для Если на некотором наборе Система имплекантов для Система имплекантов для
В общем случае минимизацию логической функции и ТДНФ можно получить методом Петрика. Все имплеканты обозначают латинскими буквами, каждый столбец дает один элемент конъюнкции, для покрывающих элементов дается дизъюнкция. Полученное выражение упрощается логическими тождествами.
Логика высказываний Логика высказываний является теорией тех логических связей, которые не зависят от структуры простых высказываний или содержания. Такая логика состоит из двух допущений: всякое высказывание является либо истинным, либо ложным с отсутствием других вариантов и значение истина сложного высказывания зависит от значений, входящих в него простых высказываний и от характера связей. Сложные высказывания состоят из простых высказываний, объединенных с помощью логических операций. Такие операции аналогичны логическим функциям и их можно описать формулой с участием простых логических операций и эту формулу рассматривать как логическую функцию нескольких переменных. Если высказывание является верным при любых значениях переменных, тогда данное высказывание называется тавтологией. Основные виды связок высказываний, при участии простых высказываний А и B: 1. Отрицание вида «НЕ A»; 2. Конъюнкция вида «A и B», «A, но B» или «A, а B»; 3. Дизъюнкция вида «A или B»; 4. Строгая дизъюнкция вида «A либо B»; 5. Эквиваленция вида «A если и только если B» или «для A необходимо и достаточно B» - для логических тождеств; 6. Импликация вида «если A, то B», «для B достаточно A» или «B является необходимым для A»; 7. Скобки – изменяют порядок действий, допуская более сложные высказывания с применением перечисленных. Истинность или непротиворечивость сложного высказывания не учитывает действительную верность входящих в него простых высказываний, которые могут содержать совершенно незнакомые понятия или несуществующие явления. В математике уравнение с двумя переменными задают прямые на плоскости, в пространстве – цилиндрическую поверхность с прохождением через эту прямую вдоль этой оси. Тогда координаты любой плоскости в случае верного равенства входят в лини через эти точки. Например, для заданной системы двух неравенств с двумя переменными
Решением является множество всех пар Системы неравенств и уравнений можно задать конъюнкцией
Эту же область можно задать соотношением значений и переменных. Логическим выражением также можно описать необходимую область на плоскости. Предикат – высказывание с логическим значением и его зависимостью от одной или нескольких переменных. Природа переменных даже в одном предикате может быть самой разнообразной. При определенном наборе значений переменных получим одно значение предиката. Для обозначения переменных используются специальные символы – кванторы. Кванторы подразделяются на два основных вида: квантор всеобщности
Связь между унарными предикатами и их отрицаниями и наличием двух видов кванторов описывается логическим квадратом следующего вида
Диагонали квадрата тожественны. В каждой строке имеется отношение подчиненности, когда из общеутвердительного следует часто отрицательное. Ошибочно такую импликацию обращать, поскольку обратное утверждение неверно. По столбцам взаимной связи в общем случае нет. Если для многоместного предиката распространяется действие нескольких кванторов, тогда однотипные кванторы можно переставлять
Преставление кванторов разного вида меняет смысл высказывания. Можно для множеств значений переменных указывать их подмножества, для элементов которых высказывания с кванторами будет верным, получая их область истинности.
Основные понятия теории алгоритмов Алгоритмом называется конечный набор четких не двусмысленных инструкций, следуя которым можно по входным данным определенного типа получить нужный результат. Для некоторых задач можно найти решение, указанное в виде алгоритма. В большинстве случаев описания задач являются неформальными и переход к алгоритмам требует верификации и многократных итераций, чтобы приблизится к результату. Верификаций называется проверка или способ подтверждения алгоритмов путем сопоставления данных. Исходя из этого, тестирование – процесс, применяемый заданным спецификациям для проверки правильности алгоритма. Одним из примеров является представление алгоритма регулярным языком. Задача формируется как разработка алгоритма для распознавания принадлежности к конкретному регулярному языку. Регулярный язык может быть формально преобразован к виду модели решения задачи за конечное число шагов – модель конечного автомата. Расширение регулярных языков находит применение при писании формальных алгоритмических языков при описании алгоритмов в современном программировании. Алфавитом языка является не пустое конечное множество символов языка. Слово алфавита
Для каждого конечного слова 1. Операция конкатенации 2. Операция объединения 3. Операция итерации слов – повторение одного или нескольких элементов
В общем случае алгебраическая формула содержит перечисленные действия с возможным использованием скобок. Языки, определяемые регулярными выражениями, называются регулярными языками. Для каждого регулярного языка можно построить хотя бы одно регулярное выражение, для каждого регулярного выражения существует только одно регулярное множество.
Конечные автоматы Конечными автоматами называется следующая совокупность
В данном соотношении Функцию переходов можно представить в виде таблицы или графически. В таблице каждой паре состояния Конечный детерминированный автомат можно изобразить графически (рисунок 67), где вершины – возможные состояния, стрелки от каждой вершины показывают переход в новое состояние под действием соответствующей буквы входного алфавита. Иногда треугольник задает начальное состояние, а двойной круг показывает конечное состояние.
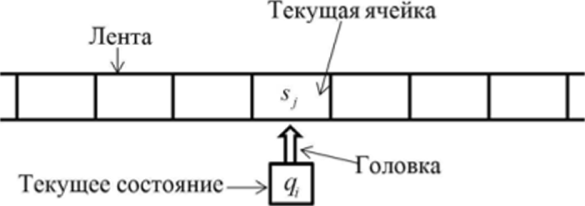
Рисунок 67. Графическое представление детерминированного конечного автомата. При большом количестве состояний, будет большое количество стрелок, также увеличение букв влечет увеличение стрелок. Конечный автомат можно изображать в виде машины как представлено на рисунке 68. В данном случае не только для одного символа, но и для слова в алфавите
Рисунок 68. Конечный автомат в виде машины. Слово из
|
||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.46.18 (0.031 с.) |
 от n переменной имеется
от n переменной имеется  различных ДНФ.
различных ДНФ.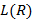 , определенная как множество всех ДНФ такой функции и обладающая следующими свойствами:
, определенная как множество всех ДНФ такой функции и обладающая следующими свойствами: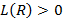 ;
;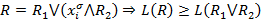 ;
; ;
;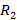 и
и 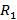 переименованием элементов без отождествления, тогда
переименованием элементов без отождествления, тогда  .
.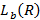 – число переменных, встречающихся в формуле M;
– число переменных, встречающихся в формуле M;  – число элементарных конъюнкций в таком R для одного дизъюнкта – ранг логической функции;
– число элементарных конъюнкций в таком R для одного дизъюнкта – ранг логической функции; 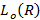 – число символов отрицаний переменных в записи R.
– число символов отрицаний переменных в записи R.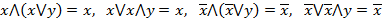

 ячеек со значениями функции в каждой из них. Ячейки сгруппированы так, что соединение ячейки описывается соседними произведениями переменных, отличающихся разными значениями. Два вида отличаются только обозначениями ячеек: карты Вейча – ячейки обозначаются названием переменных или отрицанием; карты Карно – отдельно указываются переменные и ячейки обозначаются набором из 0 и 1. Пример способа минимизации логической функции с помощью карт Карно представлен на рисунке 66.
ячеек со значениями функции в каждой из них. Ячейки сгруппированы так, что соединение ячейки описывается соседними произведениями переменных, отличающихся разными значениями. Два вида отличаются только обозначениями ячеек: карты Вейча – ячейки обозначаются названием переменных или отрицанием; карты Карно – отдельно указываются переменные и ячейки обозначаются набором из 0 и 1. Пример способа минимизации логической функции с помощью карт Карно представлен на рисунке 66.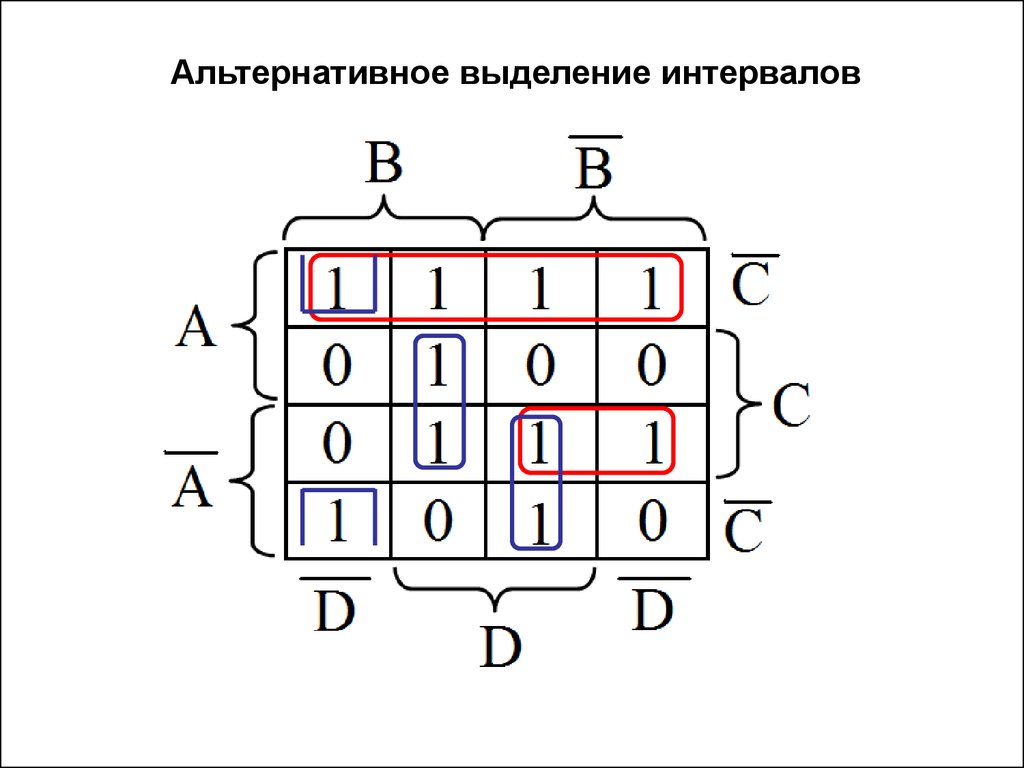
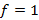 , тогда в таких дизъюнктах ранга n по закону склеивания записывается один с отсутствием переменной с различными значениями в этих клетках, получая ранг
, тогда в таких дизъюнктах ранга n по закону склеивания записывается один с отсутствием переменной с различными значениями в этих клетках, получая ранг 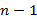 . При этом внешние границы попарно объединяются, таким образом, что можно проиллюстрировать их склеиванием в трехмерном пространстве.
. При этом внешние границы попарно объединяются, таким образом, что можно проиллюстрировать их склеиванием в трехмерном пространстве. ;
;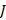 исключает выполнение свойства 1.
исключает выполнение свойства 1.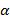 – значений переменных
– значений переменных 
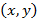 , при которых каждое неравенство является верным. В данном случае решением системы неравенств являются две полуплоскости с границами
, при которых каждое неравенство является верным. В данном случае решением системы неравенств являются две полуплоскости с границами 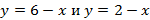 соответственно.
соответственно.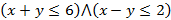
 и квантор существования
и квантор существования 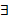 . В сложных высказываниях встречаются отрицания этих кванторов. Привала отрицания да предикатов и кванторов имеют вид
. В сложных высказываниях встречаются отрицания этих кванторов. Привала отрицания да предикатов и кванторов имеют вид
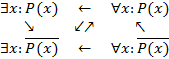

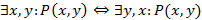
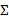 – конечная последовательность элементов алфавита, имеющее длину
– конечная последовательность элементов алфавита, имеющее длину 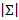 – натуральное число, равное количеству символов в слове, при этом
– натуральное число, равное количеству символов в слове, при этом 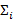 – символ с номером i в слове
– символ с номером i в слове 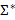 конструктивными объектами является конструктивным пространством. Множество всех слов в алфавите называется языком. Язык в конечном алфавите может содержать неограниченное число слов, для определения которых используют формальные правила:
конструктивными объектами является конструктивным пространством. Множество всех слов в алфавите называется языком. Язык в конечном алфавите может содержать неограниченное число слов, для определения которых используют формальные правила: – соединение слов
– соединение слов  , при этом
, при этом  ;
;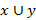 – для слов
– для слов 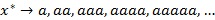
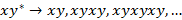

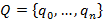 – конечное множество состояний;
– конечное множество состояний; 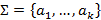 – конечное множество входного алфавита;
– конечное множество входного алфавита;  – функция переходов, которая каждой паре состояния и букве алфавита ставит в соответствие допустимое состояние; S – начальное состояние; F – множество конечных или законченных состояний.
– функция переходов, которая каждой паре состояния и букве алфавита ставит в соответствие допустимое состояние; S – начальное состояние; F – множество конечных или законченных состояний.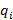 и букве
и букве 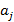 ставится в соответствие
ставится в соответствие  . Если значение этой функции задано при любом наборе
. Если значение этой функции задано при любом наборе 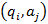 , тогда конечный автомат называют детерминированным. Если к каждой паре
, тогда конечный автомат называют детерминированным. Если к каждой паре 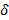 , тогда автомат полностью определенный.
, тогда автомат полностью определенный.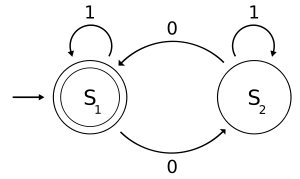
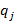 является конечным для F.
является конечным для F.


