
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное уравнение энергии
( Уравнение теплопроводности для ДВИЖУЩЕЙСЯ жидкости ) В дифференциальное уравнение конвективной теплоотдачи входит температурный градиент Решение дифференциального уравнения энергии, которое в общем виде описывает процесс переноса тепла в движущейся однофазной среде, позволяет получить распределение температур в потоке жидкости.

Имеем поток жидкости с некоторым произвольным распределением температуры Т(x, y, z, t), и скорости Рассмотрим элементарный объем dV, представляющий собой прямоугольный параллелепипед с ребрами dx, dy, dz - dV = dx × dy × dz и связанный с неподвижной системой координат x, y, z. Составим баланс тепла для этого элементарного объема, т.е. на основании закона сохранения энергии приравняем разность между поступившим и вышедшим из параллелепипеда количеством тепла к изменению энтальпии жидкости в объеме этого параллелепипеда. В направлении оси х в параллелепипед за время d t поступает следующее количество тепла dQx = qx × dy × dz × d t, через противоположную грань выходит dQx+dx = qx+dx × dу × d z × d t, где плотность теплового потока этой грани находят путем разложения в ряд Тейлора. qx+dx = qx + Отсюда разность между количеством тепла поступившим в параллелепипед и вышедшим из него в направлении оси х. dQx - dQx+dx = - Для осей y и z уравнения аналогичны. qx q y qz - проекции вектора плотности теплового потока на оси координат. Следовательно, общая разность между поступившим и вышедшим из параллелепипеда количеством тепла равна d3Q = - или dQ = -div С другой стороны, изменение теплосодержания жидкости в объеме dV за время d t составляет dQ3 = r × cP × dV × где сР - удельная теплоемкость при постоянном давлении. Приравнивая на основании закона сохранения энергии правые части (3) и (4) получим после сокращений
r × сР Процесс переноса тепла через объем параллелепипеда обусловлен во первых за счет молекулярной теплопроводности
и во вторых - конвективным переносом, обусловленным перемещением тепла с движущейся жидкостью qКОН = r × сР × Таким образом, для каждой точки в потоке жидкости плотность теплового потока равна сумме этих двух величин, (6) (7). q = r × cP × или для компонент вектора плотности теплового потока qX = r × cP × аналогично для qY и qZ. Подставляя выражение (8) в уравнение (5) получим с учетом уравнения неразрывности
где а = l / ср × r - коэффициент температуропроводности, м2 / с,
Полученное выражение (9) называется уравнением энергии, или уравнение переноса тепла в движущейся несжимаемой среде, или уравнение Фурье-Кирхгофа, или уравнение теплопроводности для движущейся жидкости. Левая часть уравнения (9), представляет собой полную производную температуры по времени, и включает изменение температуры в данной точке во времени Полученное уравнение позволяет при использовании соответствующих краевых условий и при известном распределении вектора скорости рассчитать распределение температуры в потоке жидкости и в частности вблизи поверхности твердого тела. Следовательно, для определения распределения вектора скорости надо использовать уравнения, которые бы описывали изменение скорости во времени и пространстве. Такими уравнениями являются дифференциальные уравнения движения. Уравнение движения Приведем уравнение движения без вывода в проекции только на ось х.
где g Х - проекция ускорения силы тяжести на ось х, Р - давление жидкости, n - коэффициент кинематической вязкости.
Аналогично можно написать проекции уравнения движения на оси у и z. Это уравнение Навье - Стокса. Поскольку в уравнение движения входит неизвестная величина Р, то необходимо еще одно уравнение. Таким уравнением является уравнение неразрывности (сплошности). Уравнение неразрывности Для несжимаемой жидкости (r = const) оно имеет вид
или, что то же самое div Тогда процесс конвективного теплообмена в однородной несжимаемой среде описывается следующей системой дифференциальных уравнений.
1). 2). 3). где i = x; y; z. 4). Эта система дифференциальных уравнений позволяет получить бесчисленное количество решений. Для того чтобы получить единственное решение, необходимо к системе дифференциальных уравнений присоединить условия однозначности, которые конкретизируют задачу и позволяют получить единственное решение. Условия однозначности конвективного теплообмена состоят: из геометрических условий - характеризующих форму и размеры тела или системы, в которой протекает процесс; физических условий - характеризующих физические свойства среды; временных или начальных условий - характеризующих особенности процесса в начальный момент времени (для стационарных задач эти условия отпадают); граничных условий - характеризующих протекание процесса на границах жидкой среды. Тепловой пограничный слой
Понятие теплового пограничного слоя по существу аналогично понятию гидродинамического пограничного слоя. Рассмотрим пограничный стационарный ламинарный поток жидкости, направленный вдоль плоской поверхности. Температура среды до передней кромки пластины постоянна по координате у и равна Тж. Температурное поле является стационарным. Вследствие теплообмена между слоями жидкости, расположенными вблизи поверхности пластины и поверхностью, температура слоев изменяется. Среда на поверхности пластины имеет температуру пластины. На расстоянии d т температура среды изменяется от Тпов на поверхности до температуры невозмущенного потока Тж. Расстояние d т представляет собой толщину теплового пограничного слоя. По мере удаления от передней кромки пластины толщина теплового пограничного слоя растет, т.к. охлаждающее ( или нагревающее ) влияние поверхности пластины распространяется вследствие теплопроводности на все новые слои среды. Таким образом, тепловой пограничный слой характеризуется тем, что в пределах его толщины имеет место градиент температуры, и, следовательно, перенос тепла поперек потока путем молекулярной теплопроводности. Толщина теплового пограничного слоя является функцией координаты х, возрастая по мере удаления от передней кромки пластины. Представляет интерес вопрос о соотношении толщин гидродинамического и теплового пограничных слоев при ламинарном движении среды. Поскольку возникновение пограничного слоя обусловлено переносом соответствующей субстанции ( количество движения, тепла ) поперек потока, толщина его должна определяться интенсивностью процесса переноса. Характеристиками интенсивности этих процессов являются коэффициенты переноса, т.е. кинематический коэффициент вязкости n (перенос импульса ) и коэффициент температуропроводности а ( перенос тепла ).
Следовательно, соотношение толщин гидродинамического пограничного слоя и теплового пограничного слоя должно зависеть от соотношения соответствующих коэффициентов переноса. Безразмерная величина, равная отношению этих коэффициентов, носит название критерия Прандтля, Pr = n / а. Очевидно, что чем больше величина критерия Прандтля, тем интенсивнее происходит поперечный перенос импульса, по сравнению с поперечным переносом тепла, и тем, следовательно, больше толщина гидродинамического пограничного слоя по сравнению с толщиной теплового пограничного слоя. Критерий Прандтля для газов практически не зависит ни от давления ни от температуры и определяется лишь атомностью газа. Так, для одноатомных газов Pr» 0,67, для двухатомных ~ 0,73, для трехатомных ~ 0,80. 51.уравнение теплового пограничного слоя. ланарное движение Основное значение понятий теплового и гидродинамического пограничных слоев заключается в том, что эти понятия позволяют упростить и, следовательно, решить исходные уравнения энергии. Запишем уравнение энергии для стационарного, двумерного температурного поля в движущейся несжимаемой жидкости, т.е.
Очевидно, что в связи с малой толщиной пограничного слоя, все величины в нем изменяются по толщине значительно быстрее, чем по его длине, т.е.
известное под названием уравнения Польгаузена. Если учесть, что в соответствии с постулатом Фурье плотность теплового потока в рассматриваемом случае выражается как
то уравнение (11) можно представить в виде
Решая уравнения (11) при известном заранее распределении скоростей в пограничном слое и при очевидных граничных условиях:
можно получить распределение температур в пограничном слое, а, следовательно, найти плотность теплового потока на поверхности.
|
|||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.168.2 (0.023 с.) |
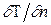 . Чтобы его найти, нужно вычислить поле температур.
. Чтобы его найти, нужно вычислить поле температур.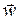 (x, y, z, t), считая, что жидкость несжимаема (r = const), скорость движения не слишком высока,что позволяет не учитывать выделение тепла вследствие вязкого трения, внутренние источники тепла отсутствуют, теплофизические свойства жидкости постоянны.
(x, y, z, t), считая, что жидкость несжимаема (r = const), скорость движения не слишком высока,что позволяет не учитывать выделение тепла вследствие вязкого трения, внутренние источники тепла отсутствуют, теплофизические свойства жидкости постоянны. dx.
dx. , (3)
, (3)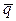 × dV × d t.
× dV × d t. × d t, (4)
× d t, (4) (5)
(5) (6)
(6) (7)
(7) ,
, , (8)
, (8) , (9)
, (9)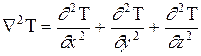 .
. - локальное изменение температуры; и изменение температуры, вызванное перемещением этой точки в поле переменной температуры вместе с движущейся жидкостью - конвективное изменение температуры
- локальное изменение температуры; и изменение температуры, вызванное перемещением этой точки в поле переменной температуры вместе с движущейся жидкостью - конвективное изменение температуры  . Эта величина называется субстанциональной производной температуры по времени.
. Эта величина называется субстанциональной производной температуры по времени. ,
, ,
, = 0.
= 0.



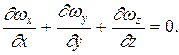

 ;
;  .
.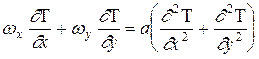 (10)
(10) , поэтому, пренебрегая величиной
, поэтому, пренебрегая величиной  , получаем более простое уравнение энергии для ламинарного пограничного слоя.
, получаем более простое уравнение энергии для ламинарного пограничного слоя. , (11)
, (11) ,
,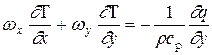 (12)
(12) (13)
(13)


