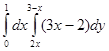Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление двойного интеграла в декартовой системе координат
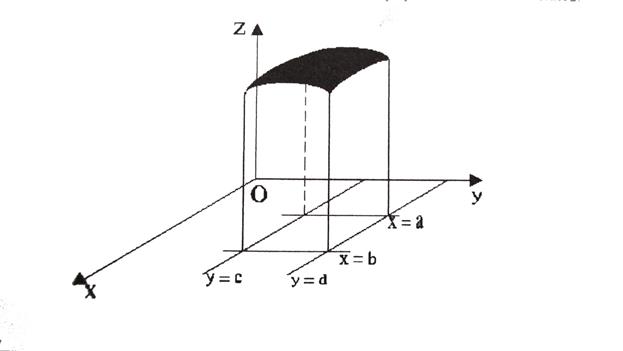
А) Пусть функция f(x,y) непрерывна в области D. Если D прямоугольник, то при вычислении двойного интеграла, при a ≤ x ≤ b, c ≤ y ≤ d имеет место формула (рис. 3.1):
которая показывает, что порядок интегрирования можно менять.
Рис 3.1 Б) Если функция f(x,y) непрерывна на множестве (рис.3.2) D= Где
Рис 3.2 Рис.3.3
Правая часть в (3.1) называется повторным интегралом, то есть результатом последовательного вычисления сначала интеграла по y при фиксированном x, а затем интеграла по x от получившейся функции. В) Если функция f(x,y) непрерывна в области D (рис.3.3) D= D= {(c≤y≤d, x1(y) ≤x≤ x2(y)} Где функции
Г) Если область D такова, что к ней применима и формула (3.1), и формула (3.2), то верно равенство:
Это равенство используется для перемены порядка интегрирования в повторном интеграле. Области более сложного вида следует разбить на части, к которым применимы формулы (3.1) или (3.2). Следует обратить внимание на то, что если y внешнего интеграла пределы интегрирования всегда константы, то у внутреннего – функции внешней переменной. Пример: изменить порядок интегрирования в интеграле
В рассматриваемом примере следует начинать с построения области интегрирования, поскольку интегралы заданы с указанием порядка интегрирования и заданы пределы по соответствующим переменным. Напомним, что переменные пределы интегрирования внутреннего интеграла являются границами изменения х при фиксированном y. Поэтому область интегрирования x=- Пусть D=
Рис. 3.4 Рис.3.5 При перемене порядка интегрирования область D можно представить полностью находящейся в вертикальной полосе при -1 ≤ x ≤ 2. Сверху область интегрирования ограничена дугой окружности (верхний предел).
Снизу область интегрирования ограничена дугой параболы (нижний предел). Тогда двойной интеграл можно записать так:
Заметим, что перемена порядка интегрирования в повторном интеграле иногда существенно упрощает его вычисление.
Пример: вычислить интеграл
При каждом фиксированном значении y, интегрирования
Вычислим внутренний интеграл
Интегрируя теперь функцию
При вычислении интеграла
Используем формулу интегрирования«по частям»
Пример: изменить порядок интегрирования
В соответствии с представленными интегралами видим, что области
Рис.3.6 B (7; 3), С(9,1)
Как видно из рис. 3.6 вся суммарная область D находится в горизонтальной полосе, поэтому целесообразно записать двойной интеграл в соответствии с формулой (3.2). Пределы интегрирования по у от 1 до 3, левая граница – гипербола
I =
Пример: вычислить двойной интеграл
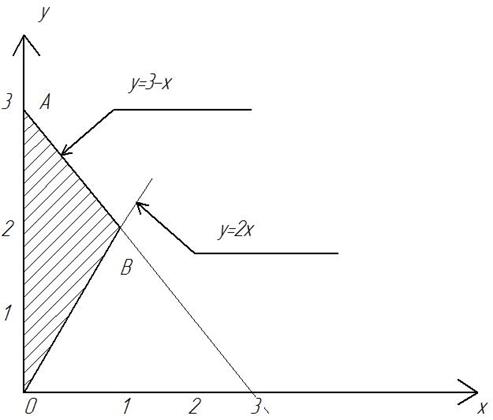
I = х=0, х + у =3, у= 2х
Рис.3.7 Строим область интегрирования: x=0 – ось Оy, y=2x – прямая. Угловые точки области: О (0; 0), A (0, 3), B (1,2) D Вся область D находится в вертикальной полосе, т.е. целесообразно записать интеграл, согласно формуле (3.1). Поэтому двойной интеграл запишется через повторный так: I=
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.124.244 (0.008 с.) |
 ,
,
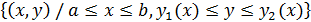
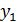 (x) и
(x) и  – непрерывны на отрезке
– непрерывны на отрезке  и
и 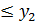 (x) на
(x) на 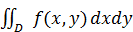 =
=  (3.1)
(3.1)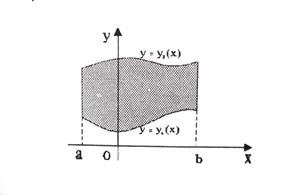

 и
и 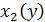 непрерывны на сегменте
непрерывны на сегменте  )
)  на [c,d], то верно равенство:
на [c,d], то верно равенство: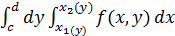 (3.2)
(3.2) (3.3)
(3.3) 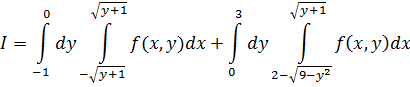
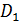 для первого интеграла при -1≤y≤0 находится между дугами параболы y = x²- 1, лежащими ниже оси Оx. Область интегрирования во втором интеграле при 0≤y≤3 ограничена кривыми
для первого интеграла при -1≤y≤0 находится между дугами параболы y = x²- 1, лежащими ниже оси Оx. Область интегрирования во втором интеграле при 0≤y≤3 ограничена кривыми и x=2
и x=2 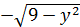 , которые представляют собой дугу параболы
, которые представляют собой дугу параболы 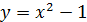 и дугу окружности
и дугу окружности  , лежащие выше оси Ox.
, лежащие выше оси Ox.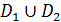

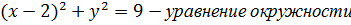


 , где область D ограничена линиями:
, где область D ограничена линиями: и y=0 (рис. 3. 5)
и y=0 (рис. 3. 5) значение x меняется от
значение x меняется от  до x=(2-y)e. Как видно из рис.3.5, наиболее удобный порядок
до x=(2-y)e. Как видно из рис.3.5, наиболее удобный порядок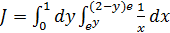

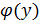 по y в пределах от y=0 до y=1, получим
по y в пределах от y=0 до y=1, получим


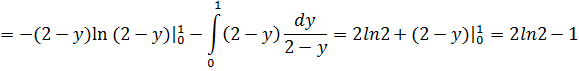 Итак, окончательно интеграл I=2ln2 – 0,5
Итак, окончательно интеграл I=2ln2 – 0,5
 расположены в вертикальных полосках при 3
расположены в вертикальных полосках при 3  и при
и при  . Причем область
. Причем область  ограничена снизу гиперболой
ограничена снизу гиперболой  , а сверху прямой у = 3. Область
, а сверху прямой у = 3. Область  также ограничена снизу той же гиперболой
также ограничена снизу той же гиперболой  Точки: А (3; 3)
Точки: А (3; 3) 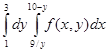
 f (x, y) = 3x-2; а область D ограничена прямыми
f (x, y) = 3x-2; а область D ограничена прямыми