Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод наибольшего правдоподобия
Метод наибольшего правдоподобия, или алгоритм максимального правдоподобия обеспечивает при отсутствии информации о стоимостях и априорных вероятностях принятия решения принятие той из гипотез, которой соответствует бóльшее значение функции правдоподобия выборки [20, с. 330]. Этот метод можно рассматривать как частный случай метода минимального риска. Алгоритм максимального правдоподобия совпадает с оптимальным алгоритмом по критерию максимума апостериорной вероятности в том случае, когда гипотеза и альтернатива равновероятны. Поэтому граничной значение x 0 определяется из условия минимума ошибки без учета априорных вероятностей и стоимостей принятия решений следующим выражением:
Этот метод преобразуется из метода минимального среднего риска при условии, что потери при совершении ошибки обратно пропорциональны вероятности их совершения. При этом величина отношения правдоподобия выбирается таким образом, чтобы минимизировать сумму вероятностей ошибок. Правило решения принимается следующим:
где x – значение параметра для диагностируемого объекта. Граничное значение х = х 0 находится из условия
Сопоставляя условия (9.5) и (11.3), легко установить, что они совпадают, если положить
В большинстве практических случаев используется условие (9.10), и тогда для метода наибольшего правдоподобия следует считать
Для задач надёжности вероятность неисправного состояния обычно представляет собой малую величину, но цена пропуска дефекта значительно больше цены ложной тревоги Пример Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение x подшипникового узла составляет Определить предельное значение x 0, рассчитать вероятность ложной тревоги, вероятность пропуска дефекта и средний риск
Решение. Так как сумма вероятностей исправного и неисправного состояний равна 1, то
По методу наибольшего правдоподобия из (11.3) имеем условие:
Подставив полученные плотности распределения в формулу выше, получим квадратное уравнение относительно х = х 0:
Подставим известные значения и решим уравнение
Это уравнение имеет положительный корень x 0 = 72,4364°C. Проведём проверку:
Теперь найдём вероятность ложной тревоги и пропуска дефекта:
Далее найдём средний риск по формуле (9.1):
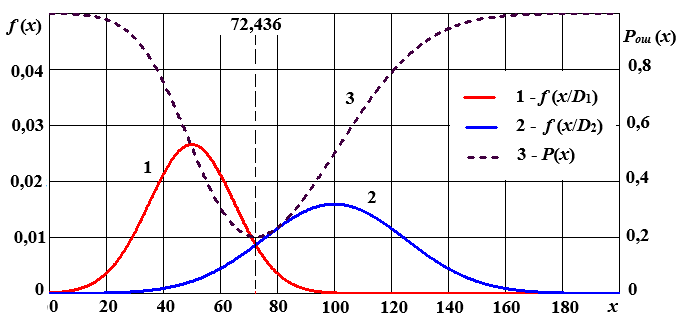
На рис. 11.1 приведены графики функций плотности вероятности, а также вероятности принятия решения P (x) (вероятность ошибки без учёта априорных вероятностей): Рис. 11.1
Рис. 11.1. Плотности распределения вероятностей и функция вероятности принятия решения P (x) без учёта априорных вероятностей Выводы. В результате расчёта по методу наибольшего правдоподобия получили предельное значение диагностического параметра x 0 = 72,436°C, выше которого исследуемый объект подлежит снятию с эксплуатации. При этом вероятность ложной тревоги составляет РЛТ = 0,0573, вероятность пропуска дефекта РПД = 0,0203. Найдена величина среднего риска, которая составляет Контрольные вопросы 1. Каков критерий метода наибольшего правдоподобия? 2. Каким образом осуществляется расчёт предельного значения? 3. Каким образом учитываются стоимости? 4. Каким образом учитываются априорные вероятности?
Метод минимакса Метод минимакса или минимаксный алгоритм [20, c.328] предназначен для ситуации, когда отсутствуют предварительные статистические сведения о вероятности диагнозов D 1и D 2. Рассматривается «наихудший случай», т.е. наименее благоприятные значения P 1и P 2, приводящие к наибольшему значению (максимуму) риска. Минимаксный критерий является частным случаем критерия Байеса, который обеспечивает минимизацию максимально возможного риска. Предположим, что величина риска зависит от x и P 1 (вероятность второго диагноза P 2 = 1 – P 1). Из соотношения (9.1) вытекает, что
Для нахождения экстремума приравниваем нулю частные производные по x и P 1. Условие
даёт
Из соотношения
получаем
Теперь требуется определить значения x 0 и P 1, удовлетворяющие уравнениям (12.3) и (12.5). Если x* 0 и P* 1 являются корнями указанных уравнений, то точка R (x 0*, P 1*) является экстремальной. Можно показать для одномодальных распределений, что величина риска становится минимаксной (т.е. минимальной среди максимальных значений, вызванных «неблагоприятной» величиной P1). При P 1 = 0и P 2 = 1риск принятия ошибочного решения отсутствует, так как ситуация не имеет неопределённости. При P 1 = 0(все объекты неисправны) из условия (9.5) вытекает Для промежуточных значений 0< P 1<1 риск возрастает и при P 1 =P* 1становится максимальным. Рассматриваемым методом выбирают величину x0 таким образом, чтобы при наименее благоприятных значениях P1 потери, связанные с ошибочными решениями, были бы минимальными. Рассмотрим процедуру решения уравнений (12.3) и (12.5). Сначала из уравнения (12.5) найдём значение x* 0, что можно сделать следующим образом. Представим уравнение (12.5) в виде
где
Последнее равенство можно записать с помощью функций распределения
Для определения х 0 уравнение (12.6) решаем по методу Ньютона, связывающему исходные x 0(n -1) и последующие x 0(n) приближения
Значение производной
В качестве первого приближения можно принять
Величину риска определяем по равенству (12.1) при значениях x 0 =x * 0, P 1 =P * 1. Отметим некоторые случаи, в которых решение становится достаточно наглядным. Положим, что условные выигрыши отсутствуют C 11= C 22=0, а цены ошибок одинаковы C 12= C 21. Тогда из уравнения (12.5) вытекает
где f (x/D 1) и f (x/D 2) – соответствующие функции распределения. Последнее соотношение показывает равенство условных вероятностей ошибочных решений. Рис. 8.1 На рисунке 8.1 для этого случая площади РЛТ и РПД равны. В общем случае
Зависимость (12.12) выражает равенство условных рисков ошибочных решений. С помощью функции распределения она записывается в виде
Пример Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение подшипникового узла составляет Определить предельное значение x 0, рассчитать вероятность ложной тревоги, вероятность пропуска дефекта и средний риск
Решение. Так как сумма вероятностей исправного и неисправного состояний равна единице, то
По методу минимакса основные соотношения имеют вид (12.3), (12.8), (12.10):
Решаем уравнение методом Ньютона путём приближений (12.9) с учётом следующих соотношений:
Первое приближение х = х 0 определяем как среднее арифметическое:
Выполняя следующие итерации по (12.9), получим:
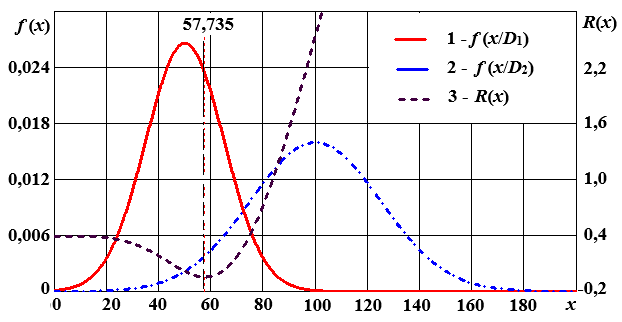
Прекращение флуктуаций величины x 0(n) после пятой итерации позволяет найти корень уравнения, который равен x 0 = 57,735°C.
Теперь найдём наиболее неблагоприятное значение вероятностей исправного и неисправного состояний P 1 и P 2 согласно (12.11).
Подставив формулу для плотности распределения, найдём вероятность ложной тревоги и пропуска дефекта:
Далее найдём средний риск по формуле:
Рассмотрим крайнюю ситуацию, когда C 12 =C 21 = 1, C 11= C 22=0 и рассчитаем новое предельное значение x 0
Прекращение флуктуаций величины x 0(n) после третьей итерации позволяет найти корень уравнения, который равен x 0 = 68,75°C. Теперь найдём наиболее неблагоприятное значение вероятностей исправного и неисправного состояний P** 1 и P** 2 согласно (12.11).
Найдём вероятности
Далее найдём средний риск по формуле (9.1):
На рис. 12.1 приведены графики функций плотности вероятности f (x)для исправного D 1 и неисправного D 2 состояний, а также функция риска принятия решения R (x): Рис. 12.1
Рис. 12.1. Плотности распределения вероятностей и функция риска R (x) Выводы. В результате расчёта по методу минимакса получили предельное значение диагностического параметра x 0 = 57,735°C, выше которого исследуемый объект подлежит снятию с эксплуатации. При этом вероятность ложной тревоги составляет РЛТ = 0,211, вероятность пропуска дефекта – РПД = 0,014, а средний риск пропуска дефекта составляет R = – 0,045 C 21. При C 12 =C 21 = 1, C 11= C 22=0 предельное значение диагностического параметра есть x 0 = 68,75°C. Уточнённые вероятности Р 1 = 0,375, Р 2 = 0,625, вероятность ложной тревоги РЛТ = 0,0396, вероятность пропуска дефекта РПД = 0,066, а средний риск пропуска отказа R = 0,106 C 21. Контрольные вопросы 1. Каков критерий метода минимакса? 2. В каких случаях применяют метод минимакса? 3. Каким образом находят экстремум? 4. Какой метод используют для решения уравнения и определения граничного значения?
Метод Неймана - Пирсона Во многих практических ситуациях и реальных условиях применения вероятностно-статистических методов принятия решения при оценке риска принятия ошибочного решения бывает затруднительно предсказать достаточно реалистические стоимости и априорные вероятности. Эту трудность можно довольно просто обойти, если иметь дело с условными вероятностями ложной тревоги и обнаружения цели (дефекта). Вообще говоря, хотелось бы сделать РЛТ как можно меньше, а (1– РПД) как можно больше. В большинстве задач, имеющих практическое применение, эти цели являются противоречащими друг другу. Очевидное решение проблемы заключается в том, чтобы ограничить одну вероятность и максимизировать (минимизировать) другую.
В этом случае центр проблемы переносится на обоснованный выбор допустимого уровня ошибок с помощью предыдущего опыта или интуитивных соображений. По методу Неймана – Пирсона минимизируется вероятность пропуска дефекта при заданном допустимом уровне вероятности ложной тревоги. Таким образом, вероятность ложной тревоги должна удовлетворять условию:
где А – заданный допустимый уровень вероятности ложной тревоги; P 1 – вероятность исправного состояния. Рис. 8.1 Отметим, что обычно условие (13.1) относят к условной вероятности ложной тревоги (множитель P 1 отсутствует). В задачах технической диагностики значения P 1 и P 2 в большинстве случаев известны по статистическим данным. Из рис. 8.1 видно, что при увеличении ошибки ложной тревоги (сечение x 0 перемещается влево) величина ошибки пропуска дефекта уменьшается. Ее наименьшее значение будет соответствовать знаку равенства в (13.1):
Теперь условие (13.1) однозначно определяет величину x0 и значение риска. Остановимся на выборе значения А – допустимого уровня ложной тревоги (риска поставщика). В практических задачах можно принимать
где k – коэффициент избыточности, зависящий от разрешающей способности диагностических средств, опасности дефекта, экономических затрат и других обстоятельств. При дефектах с ограниченными последствиями можно принимать
При опасных дефектах принимают k= 3…10. Для редко встречающихся (P 2<0,01), но крайне опасных дефектов, коэффициент избыточности может достигать и больших значений. В задачах технической диагностики можно использовать и другой подход: определять граничное значение x 0, исходя из выбранной вероятности пропуска дефекта. В этом случае
где B – заданное значение вероятности пропуска дефекта. Трудно указать общие правила для назначения величины B, она должна выбираться с учётом указанных ранее соображений. Если дефект крайне нежелателен на единичном изделии, можно принимать
где N – общее число изделий, находящихся в эксплуатации; k – коэффициент избыточности (1 ≤ k < 10). Во всех случаях для реализации принципа невозможности маловероятных событий величина B должна быть малой (B <0,01). При практическом решении подобных уравнений целесообразно использовать метод Ньютона, полагая, например
Пример Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение подшипникового узла составляет Определить предельное значение x 0, рассчитать вероятность ложной тревоги, вероятность пропуска дефекта и средний риск, если известно, что
Решение. Так как сумма вероятностей исправного и неисправного состояний равна единице, то
Решим эту задачу по методу Неймана – Пирсона: За коэффициент избыточности k возьмём 1. Тогда Найдём необходимые величины для расчёта по методу Ньютона, а также плотность распределения:
Решаем уравнение по методу Ньютона:
Первое приближение определяем как среднее арифметическое:
Выполнив шесть итераций, получим:
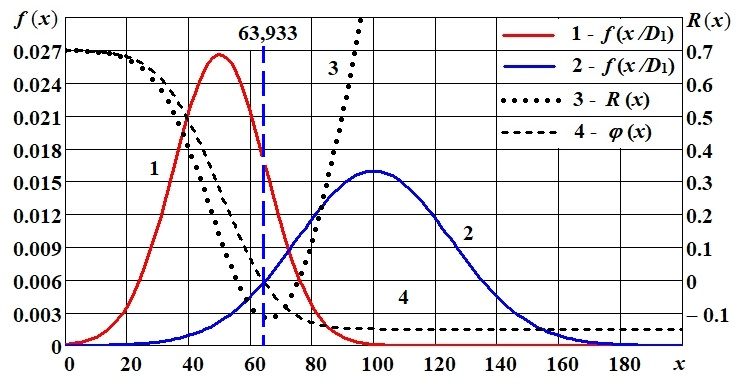
В результате корень уравнения принимается равным 63,933оC. Теперь найдём вероятность ложной тревоги и пропуска дефекта:
Далее найдём средний риск по формуле (9.1):
На рис. 13.1 приведены графики функций распределения плотности вероятностей f (x)для исправного D 1 и неисправного D 2 состояний, а также функции риска R (x) и вероятности пропуска дефекта при заданном допустимом уровне вероятности ложной тревоги φ (x):
Рис. 13.1. Плотности распределения вероятностей, Выводы В результате расчёта по методу Неймана-Пирсона получили предельное значение диагностического параметра x 0 = 63,933°C, выше которого исследуемый объект подлежит снятию с эксплуатации. При этом вероятность ложной тревоги составляет РЛТ = 0,15, вероятность пропуска дефекта РПД = 0,011, а средний риск пропуска дефекта составляет R = – 0,115 C 21. Контрольные вопросы 1. Каков критерий метода Неймана-Пирсона? 2. Каким образом находят экстремум? 3. Какой метод используют для решения уравнения и определения граничного значения?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.41.214 (0.099 с.) |
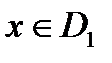 , если
, если 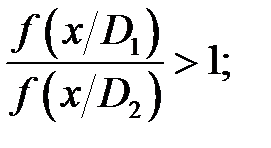
 , если
, если 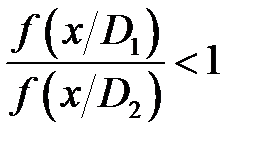 ,
,
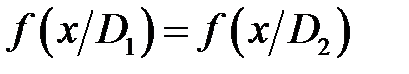 .
.
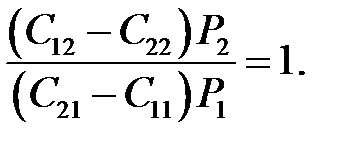

 .Тогда условие (11.5) даёт решение, не требующее знания точных значений стоимости ошибок и качественно отражающее указанные обстоятельства
.Тогда условие (11.5) даёт решение, не требующее знания точных значений стоимости ошибок и качественно отражающее указанные обстоятельства 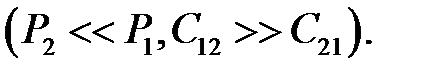
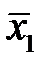 =50°C и среднее квадратичное отклонение σ 1=15°C. При наличии повышенного износа
=50°C и среднее квадратичное отклонение σ 1=15°C. При наличии повышенного износа  =100°C, σ 2=25°C. Распределения предполагаются нормальными.
=100°C, σ 2=25°C. Распределения предполагаются нормальными.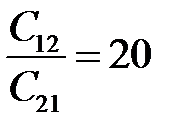 ,
, 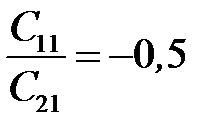 ,
, 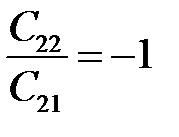 ,
, 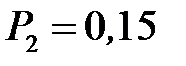 .
. .
. .
.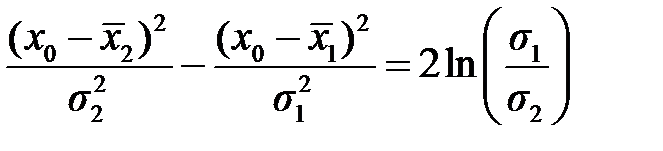 .
.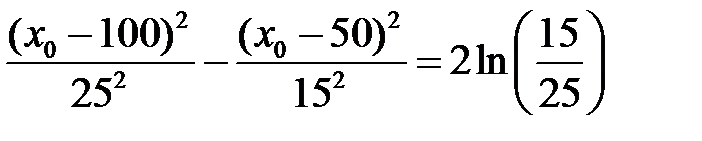 .
. ,
,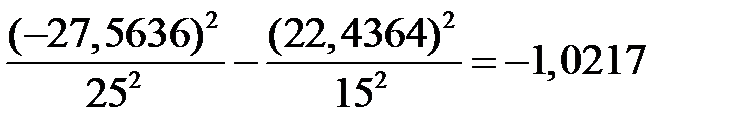 ,
,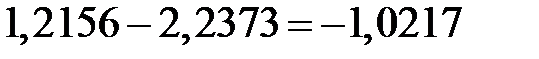 .
. ,
, .
. .
.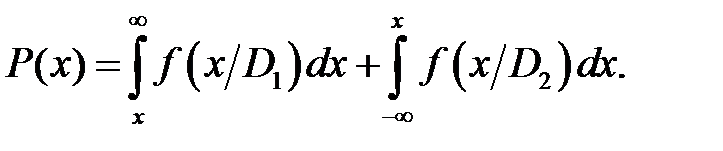
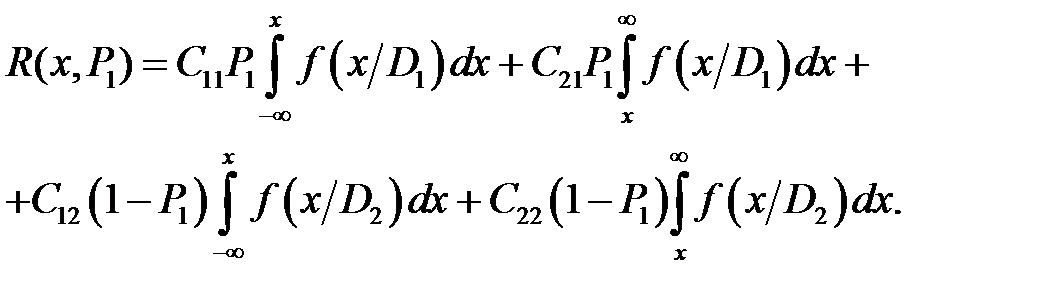
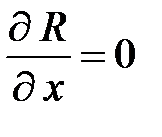
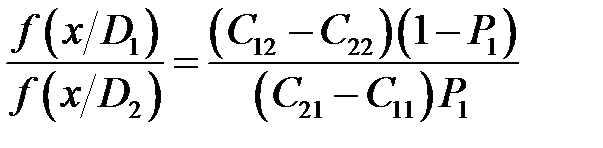 .
.

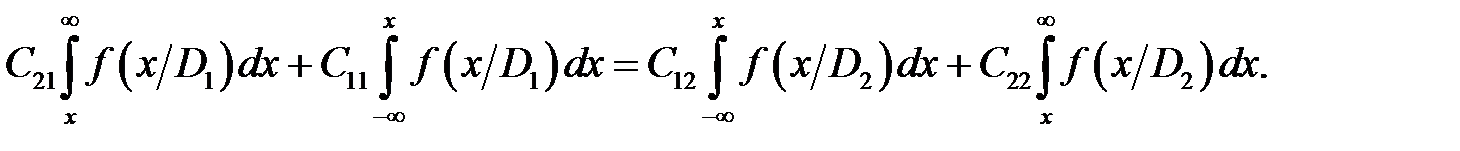
 и все объекты действительно признаются неисправными; при P 1=1 и P 2=0
и все объекты действительно признаются неисправными; при P 1=1 и P 2=0  и в соответствии с имеющейся ситуацией все объекты классифицируются как исправные.
и в соответствии с имеющейся ситуацией все объекты классифицируются как исправные.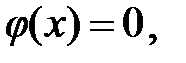
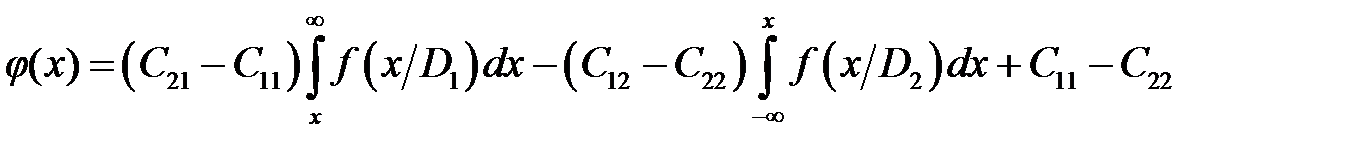 .
.
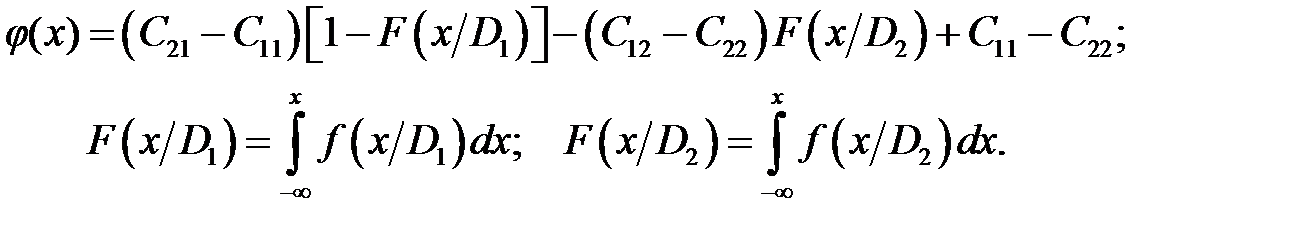
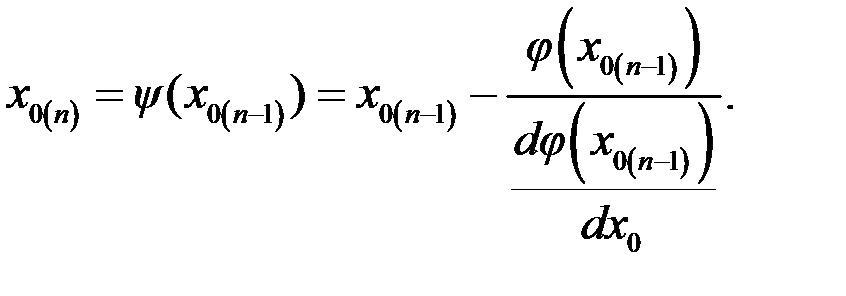
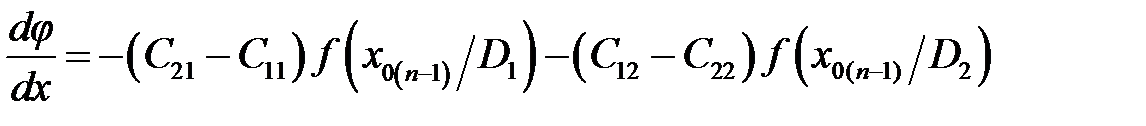 .
.
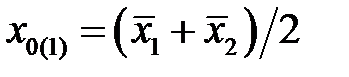 , где
, где 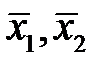 – средние значения x для распределения f (x/D 1) и f (x/D 2). При достаточной близости x 0(n) и x 0(n -1) принимаем x* 0 =x 0(n). Далее из равенства (12.3) находим наименее благоприятное значение вероятностей исправного P * 1 и P * 2 неисправного состояний
– средние значения x для распределения f (x/D 1) и f (x/D 2). При достаточной близости x 0(n) и x 0(n -1) принимаем x* 0 =x 0(n). Далее из равенства (12.3) находим наименее благоприятное значение вероятностей исправного P * 1 и P * 2 неисправного состояний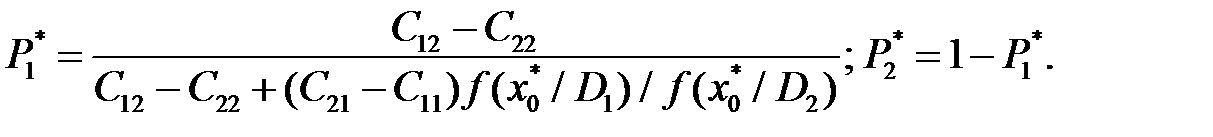
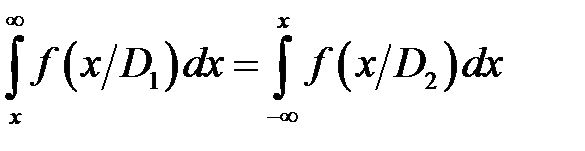 или
или 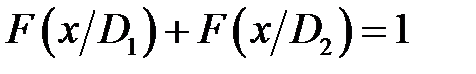 ,
,
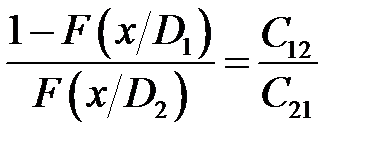 .
.
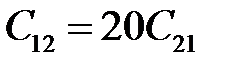 ,
, 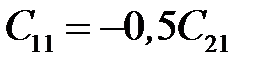 ,
, 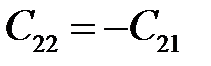 ,
,  ,
,
 ,
,
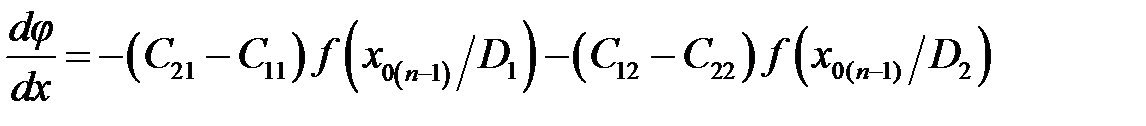 .
.
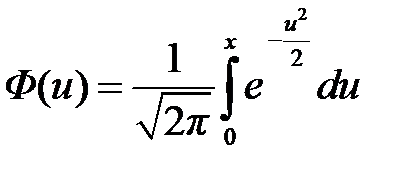 ,
, 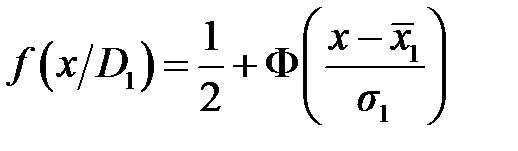 ,
, 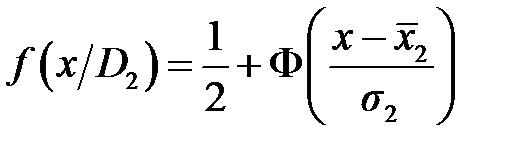 ,
, .
. ,
, 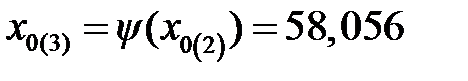 ,
, ,
, 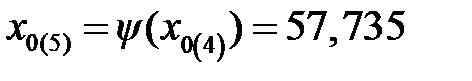 ,
, 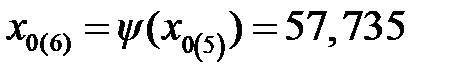 .
. ,
, 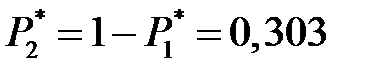 .
.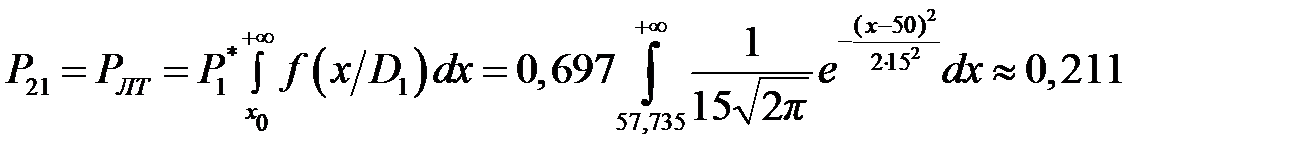 ,
,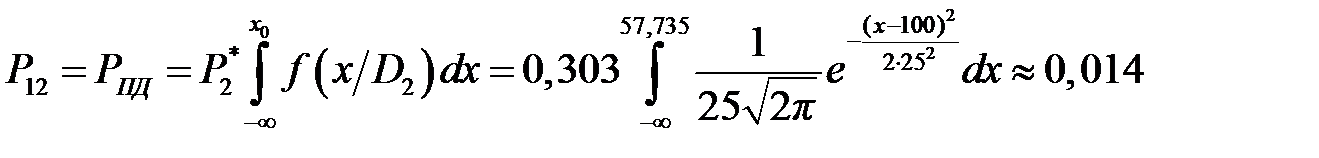 .
.
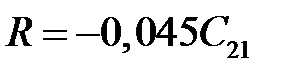 .
.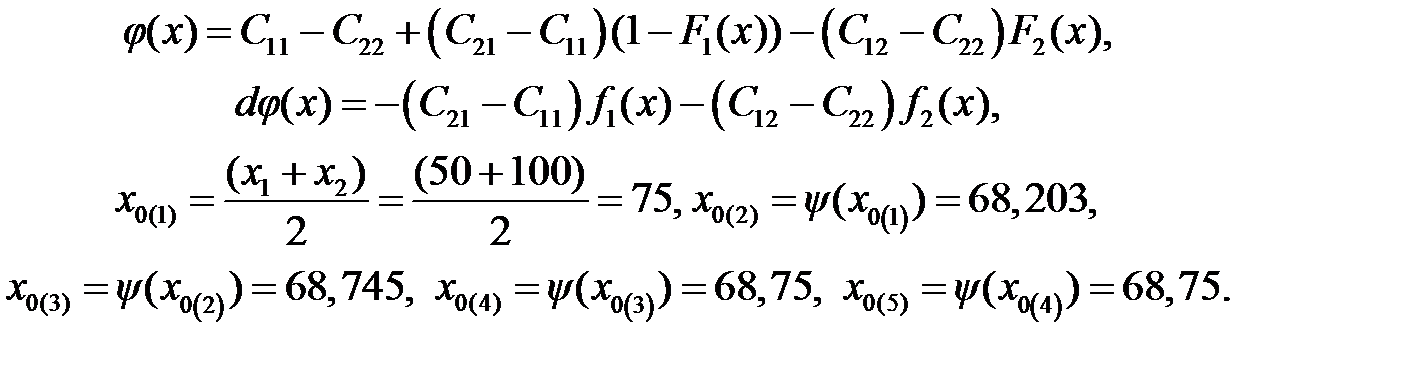
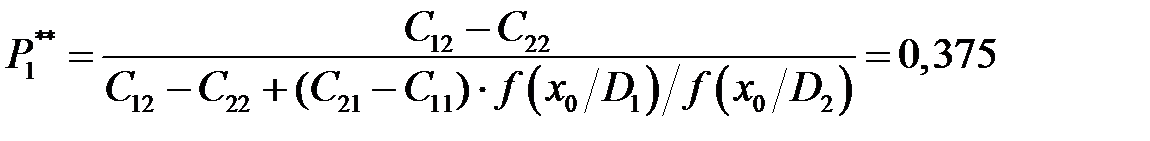 ,
, 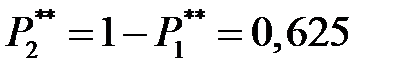 .
.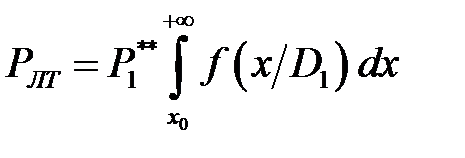 ,
, 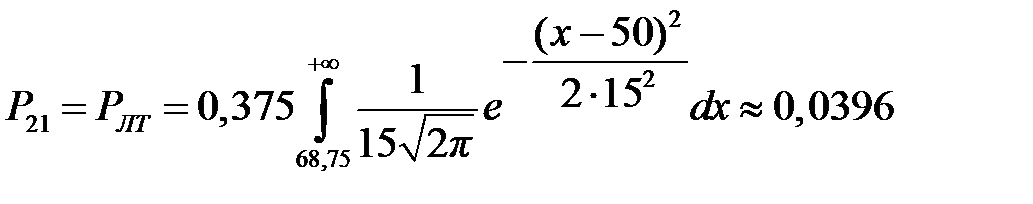 ,
,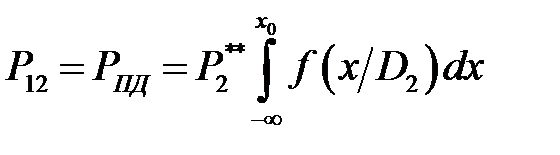 ,
, 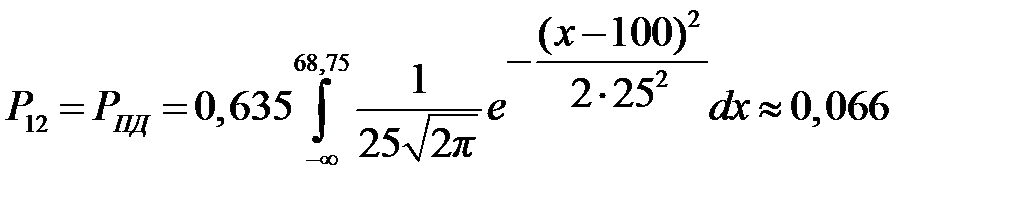 .
. .
.
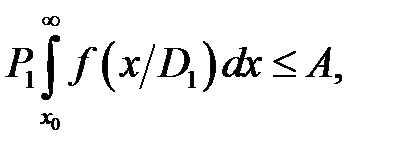

 ,
,
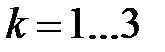 .
.
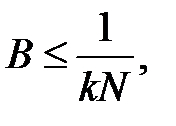
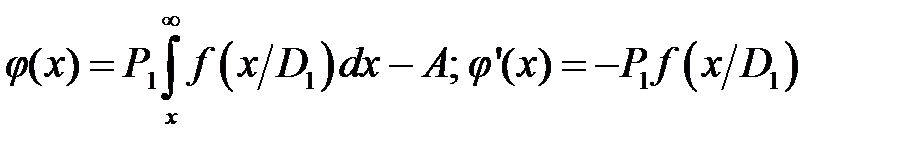 .
.
 ,
, 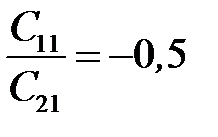 ,
, 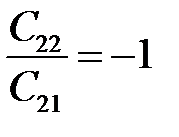 ,
,  .
.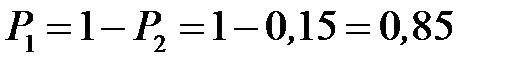 .
.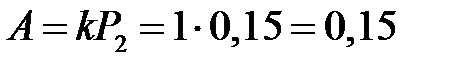 .
.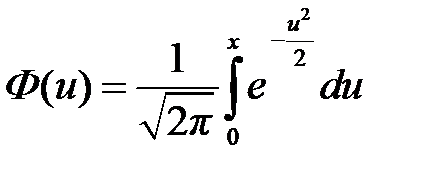 ,
, 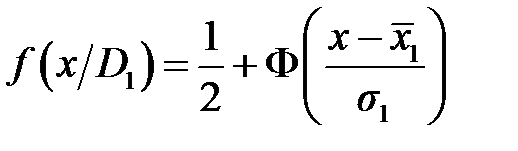 ,
, 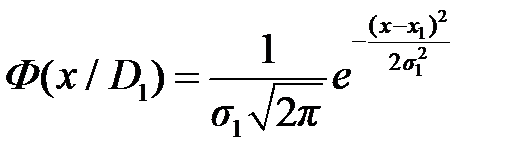 ,
, ,
,  .
.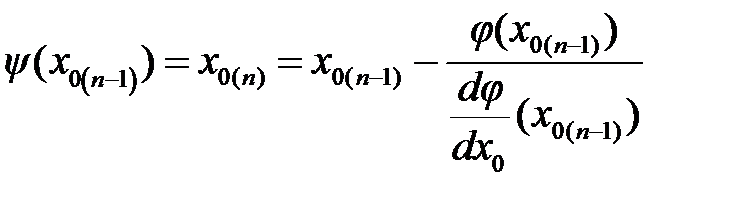 .
.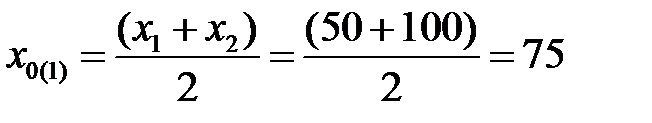 .
.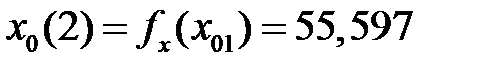 ,
,  ,
,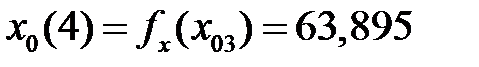 ,
, 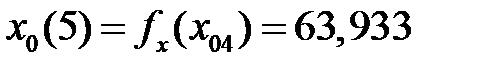 ,
, .
.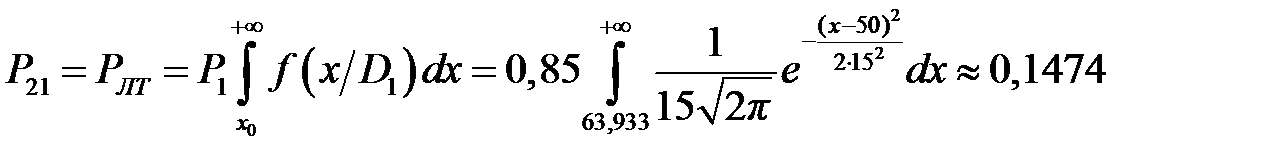 ,
,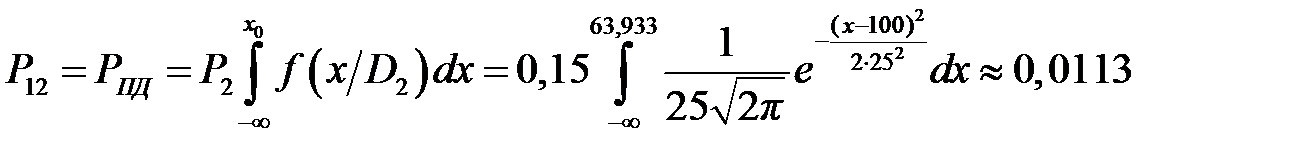 .
.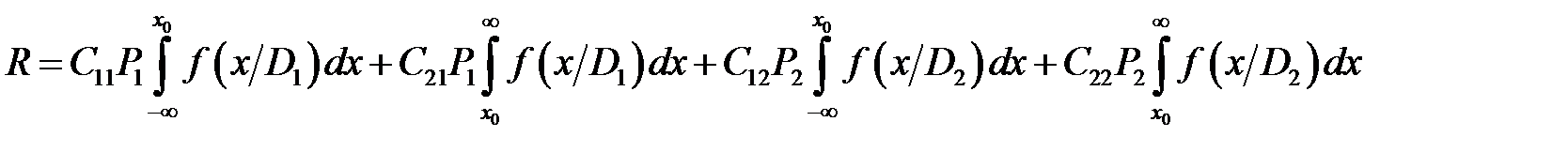 ,
,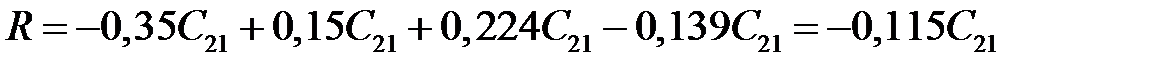 .
.