
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор пороговых значений диагностических параметров. 88
15 Задания для практических работ. 90 15.1 Задача № 1. 90 15.2 Задача № 2. 90 15.3 Задача № 3. 91 15.4 Задача № 4. 91 15.5 Задача № 5. 91 15.6 Задача № 6. 91 15.7 Дополнительные данные к задачам № 1-6. 91 Вместо заключения. 94 БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 95 Дополнительная литература. 96
ВВЕДЕНИЕ Функционирование методов и средств технической диагностики основывается на том, что в общем случае на основе совокупности диагностических признаков, каждый из которых с определённой вероятностью характеризует состояние диагностируемого объекта, необходимо сформировать решающее правило, с помощью которого выделенная совокупность признаков была бы отнесена к одному из возможных состояний (диагнозов) [1, 2]. В частном случае необходимо провести выбор одного из двух диагнозов (дифференциальная диагностика или дихотомия), например, «исправное состояние» и «неисправное состояние» [7]. В таких случаях применяются вероятностно-статистические методы принятия решений, при этом эффективность принимаемых решений зависит от факторов, представляющих собой случайные величины, для которых известны законы распределения вероятностей и другие статистические характеристики. При таком подходе каждое решение может привести только к одному из множества вероятных исходов, причём вероятность каждого исхода может быть определена расчётными методами. Параметры каждого показателя, включённого в совокупность признаков, также описываются с помощью вероятностных характеристик [19, 17]. На практике вероятностные и статистических методы часто применяются, когда сделанные на основе выборочных данных выводы переносятся на всю совокупность (например, с выборки на всю партию изделий). Однако при этом в каждой конкретной ситуации следует предварительно оценить принципиальную возможность получения достаточно достоверных вероятностных и статистических данных. Итак, суть вероятностно-статистических методов принятия решений состоит в использовании вероятностных моделей на основе оценивания и проверки гипотез с помощью выборочных характеристик [19, 17]. Основное же преимущество вероятностно-статистических методов распознавания состоит в возможности одновременного учёта признаков различной физической природы или механизмов формирования, так как эти методы оперируют безразмерными величинами – вероятностями их появления при возникновении различных состояний системы.
Среди методов технической диагностики метод, основанный на обобщённой формуле Байеса, занимает особое место благодаря простоте и эффективности. Однако этот метод обладает одним существенным недостатком – «угнетение» редко встречающихся признаков, что недопустимо в случае мониторинга состояния опасных производственных объектов [7]. Метод Вальда (метод последовательного анализа) позволяет путём приближений решить задачу по принятию решения. Однако часто в условиях реальных производств применение метода Вальда для анализа признаков при диагностировании не обеспечивает минимизации величины ошибки постановки диагноза в связи с возможностью превышения интервала постановки диагноза [7, 6, 14, 13, 10, 14]. Тем не менее его использование вполне оправдано и даже необходимо при проведении контрольных испытаний и контроле качества произведённой продукции. Такие методы вероятностно-статистических решений как минимального риска, минимального числа ошибочных решений, наибольшего правдоподобия, минимакса, Неймана-Пирсона позволяют выбрать решающее правило исходя из условий оптимальности, например, из условия минимального риска, минимизация одной из ошибок постановки диагноза при заданном уровне другой [3, 7, 8, 9, 11]. В общем виде условия принятия вероятностно-статистических решений при определении граничного значения x 0 можно сформулировать следующим образом: – метод минимального риска – добиваются минимума среднего риска; – метод минимального числа ошибочных решений – принимают стоимости пропуска дефекта и ложной тревоги одинаковыми; – метод наибольшего правдоподобия – принимают стоимость и вероятность пропуска дефекта приблизительно равными стоимости и вероятности ложной тревоги; – метод минимакса – величина риска выбирается минимальной среди максимальных значений, вызванных «неблагоприятной» величиной Pi; – метод Неймана-Пирсона – минимизируется вероятность пропуска дефекта при заданном допустимом уровне вероятности ложной тревоги.
Часто оценки стоимости ошибок неизвестны, а их достоверное определение связано с большими трудностями. Вместе с тем ясно, что во всех случаях желательно при определённом (допустимом) уровне одной из ошибок минимизировать значение другой. Поэтому центром проблем является обоснованный выбор допустимого уровня ошибок на основе предыдущего опыта или интуитивных соображений. Изучение и овладение вероятностно-статистическими методами принятия решений является существенной компетенцией специалистов в области радиотехники и приборостроения, позволяющей существенно повысить уровень решаемых задача и обеспечить высокую достоверность получаемых результатов.
Метод Байеса Среди методов технической диагностики – метод, основанный на обобщённой формуле Байеса, который позволяет определить вероятность того, что произошло какое-либо событие (гипотеза), при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточными. Метод Байеса имеет недостатки: большой объем предварительной информации, «угнетение» редко встречающихся диагнозов и др. Однако Байеса подход позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. В диагностике это позволяет «связать» диагностические признаки и повлёкшие их неисправности. События, отражающие действие «причин», в данном случае называют гипотезами, так как они — предполагаемые события, повлёкшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учётом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учётом данных о событии). Априорная вероятность – распределение вероятностей, которое выражает предположения до учёта экспериментальных данных. Другими словами, априорное распределение вероятностей неопределённой величины P – распределение вероятностей, которое выражает предположения о вероятности P до учёта экспериментальных данных.
Основы метода Метод основан на простой формуле Байеса. Если имеется диагноз Di и простойпризнак kj, встречающийся при этом диагнозе, то вероятность совместного появления событий (наличие у объекта состояния Di и признака kj) можно определить следующим образом:
Из этого равенства вытекает формула Байеса – вероятность диагноза Di при наличии признака kj:
Очень важно определить точный смысл входящих в эту формулу величин: · P (Di) – вероятность диагноза Di, определяемая по статистическим данным (априорная вероятность). Так, если предварительно обследовано N объектов и у Ni объектов имелось состояние Di, то вероятность P (Di) постановки диагноза Di определяется как
Иными словами, если в корзине было 100 шаров (N =100), из которых 40 красных (Ni = 40), то вероятность выбора красного шара составляет P (Di) = 40/100 = 0,4.
· P (kj/Di) – вероятность появления признака kj у объектов с состоянием Di. Если среди Ni объектов, имеющих диагноз Di, у Nij проявился признак kj, то
Т.е., если у 40 красных шаров (Ni = 40) 10 шаров имели синюю точку (Ni j = 10), то вероятность появления признака «синяя точка» у красных шаров составляет P (kj/Di)= 10/40 = 0,25. · P (kj) – вероятность появления признака kj во всех объектах независимо от состояния (диагноза) объекта. Пусть из общего числа N объектов признак kj был обнаружен у Nj объектов, тогда
Если из всех шаров (N =100) признак «синяя точка» имеется у 50 шаров (N j = 50), то вероятность появления этого признака при выборе шаров из корзины составляет P (kj)= 50/100 = 0,5. Следовательно, если мы выбрали шар с «синей точкой», то вероятность того, что он красный есть: P (Di / kj)= 0,4∙0,25 / 0,5=0,2. Для установления диагноза специальное вычисление P (kj) не требуется. Как будет ясно из дальнейшего, значения P (Di) и P (kj/D i), известные для всех возможных состояний, определяют величину P (kj). В равенстве (1.2) P (Di / kj) – вероятность диагноза Di после того, как стало известно наличие у рассматриваемого объекта признака kj (апостериорная вероятность диагноза).
Обобщённая формула Байеса Обобщённая формула Байеса относится к случаю, когда обследование проводится по комплексу признаков K,включающему признаки k 1 ,k 2 ,…,kv. Каждый из признаков kj имеет mj разрядов (kj 1, kj 2 ,…, kjs,…, kjm). В результате обследования становится известной реализация признака
и всего комплекса признаков K*. Индекс * означает конкретное значение признака. Формула Байеса для комплекса признаков имеет вид
где P (Di /K*) – вероятность диагноза Di после того, как стали известны результаты обследования по комплексу признаков K; P (Di) – предварительная вероятность диагноза Di (по предшествующей статистике). Формула (1.7) относится к любому из n возможных состояний (диагнозов) системы. Предполагается, что система находится только в одном из указанных состояний, и потому
В практических задачах нередко допускается возможность существования нескольких состояний А 1 ,…,Аr, причём некоторые из них могут встретиться в комбинации друг с другом. Тогда в качестве различных диагнозов Di следует рассматривать отдельные состояния D 1 =A 1 ,…, Dr=Ar и их комбинации Dr+ 1 =A 1 ∩A 2. Перейдём к определению P (Di/K*). Если комплекс признаков состоит из v признаков, то
где k*j = kjs – разряд признака, выявившийся в результате обследования. Для диагностирования по независимым признакам:
В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков даже при наличии существенных корреляционных связей между ними. Вероятность появления комплекса признаков K*
Это равенство часто называют формулой полной вероятности события К *, происходящего вместе с полной группой событий. Формула полной вероятности является фундаментальной во многих вопросах теории вероятности потому, что она отражает следующий принцип: если система имеет несколько возможных несовместных путей перехода в другое состояния, то вероятность перехода равна сумме вероятностей осуществления каждого из них. Несовместные пути (или события) – это пути (события), которые не могут реализовываться одновременно. Пример. Применение формулы полной вероятности. Прибор может иметь два режима работы, при этом в нормальном режиме работы прибор может находиться с вероятностью P (D 1)=0,8, а в ненормальном – с вероятностью P (D 2)=0,2. Вероятность поломки прибора в течение заданного интервала времени t при его работе в нормальном режиме составляет P (t / D 1)=0,1, а в ненормальном – P (t / D 2)=0,7. Найти полную вероятность выхода из строя прибора за указанный интервал времени t. По формуле (1.11) определяем
Следовательно, вероятность поломки прибора при его работе в нормальном или ненормальном режимах за интервал времени t составляет 0,22.
Обобщённую формулу Байеса можно записать в следующем виде:
где P (Di / K*)определяется равенством (1.9) и (1.10). Из соотношения (1.12) вытекает
что, разумеется, и должно быть, так как один из диагнозов обязательно реализуется, а реализация одновременно двух диагнозов невозможна. Следует обратить внимание на то, что знаменатель обобщённой формулы Байеса одинаков для всех диагнозов. Это позволяет сначала определить вероятности совместного появления данной реализации комплекса признаков и i -го диагноза
И затем апостериорную вероятность диагноза
Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. Пример. Применение формулы Байеса. Известно, что 90% подшипников качения вырабатывают ресурс в исправном состоянии. Признак k 1 – повышение температуры масла выше нормальной на 40оС – встречается у исправных подшипников в 5% случаев. Необходимо определить вероятность исправного состояния подшипника при появлении признака k 1. Примем, что D 1 – исправное состояние, а D 2 – неисправное. Положим, что известно: P (D 1)=0,9; P (D 2)=1– P (D 1)=0,1, P (k 1/ D 1)=0,05; P (k 1/ D 2)=0,95. По формуле (1.12)
Таким образом, если в процессе наблюдения за состоянием подшипника зафиксировано повышение температуры масла выше нормальной на 40оС, то вероятность исправного состояния подшипника составляет 0,32.
Если реализация некоторого комплекса признаков К* является детерминирующей для диагноза Dp, то этот комплекс не встречается при других диагнозах:
Тогда, в силу равенства (1.12)
Таким образом, детерминистская логика установления диагноза является частным случаем вероятностной логики. Формула Байеса может использоваться и в том случае, когда часть признаков имеет дискретное распределение, а другая часть — непрерывное. Для непрерывного распределения используются плотности распределения. Однако в расчётном плане указанное различие признаков несущественно, если задание непрерывной кривой осуществляется с помощью совокупности дискретных значений. Диагностическая матрица Для определения вероятности диагнозов с использованием метода Байеса необходимо сформировать диагностическую матрицу (табл. 1.1), которая составляется на основе предварительно собранного статического материала. В этой таблице содержатся вероятности разрядов признаков при различных диагнозах. В диагностическую матрицу включены априорные вероятности диагнозов. Если признаки двухразрядные, то в таблице достаточно указать вероятность появления признака P (kj/Di) =N ij / N (1.4). Таблица 1.1 Вероятность отсутствия признака
Таблица 1. 1 Диагностическая матрица
Однако более удобно использовать единообразную форму, полагая, например, для двухразрядного признака
Отметим, что Сумма вероятностей всех возможных реализаций признаков равна единице. Процесс обучения при использовании метода Байеса состоит в формировании диагностической матрицы. Важно предусмотреть возможность уточнения таблицы в процессе диагностики. Для этого в памяти
Далее вводят поправки к вероятностям признаков. Пусть у нового объекта с диагнозом Dµ выявлен разряд r признака kj. Тогда для дальнейшей диагностики принимаются новые значения вероятности интервалов признака kj при диагнозе Dµ для каждого интервала s признака kj s:
Условные вероятности признаков при других диагнозах корректировки не требуют. Решающее правило – правило, в соответствии с которым принимается решение о диагнозе. По методу Байеса объект, имеющий комплекс признаков K *, относится к диагнозу с наибольшей (апостериорной) вероятностью K ∈ Di, если
Символ ∈, применяемый в функциональном анализе, означает принадлежность множеству. Условие (1.19) указывает, что объект, обладающий данной реализацией комплекса признаков K * или, короче, реализация K * принадлежит диагнозу (состоянию) Di. Правило (1.19) обычно уточняется введением порогового значения для вероятности диагноза
где Pi – заранее выбранный уровень распознавания для диагноза Di. При этом вероятность наиболее ближайшего конкурирующего диагноза чаще всего не выше 1 – Pi. Обычно принимается Pi ≥ 0,9. При условии
решение о диагнозе не принимается (отказ от распознавания) и требуется получение дополнительной диагностической информации. Как указывалось ранее, методу Байеса присущи некоторые недостатки, например, погрешности при распознавании редких диагнозов. При практических расчётах целесообразно провести диагностику и для случая равновероятностных диагнозов, положив
Тогда наибольшим значением апостериорной вероятности будет обладать диагноз Dj, для которого P (K */ Di) максимальна
Иными словами, устанавливается диагноз Di, если данная совокупность признаков чаще встречается при диагнозе Di, чем при других диагнозах. Такое решающее правило соответствует методу максимального правдоподобия. Из предыдущего вытекает, что этот метод является частным случаем метода Байеса при одинаковых априорных вероятностях диагнозов. При использовании метода максимального правдоподобия вычисленные «частые» и «редкие» диагнозы равноправны. Вероятность пропуска цели Р (H 12) равна вероятности произведения двух событий: технический объект априорно имеет вероятность P (D 2) нахождения объекта в состоянии с диагнозом D 2, но по результатам диагностического обследования он отнесён к другому диагнозу D 1 с вероятностью P (D 1/ K):
Таким образом, Р (H 12) показывает вероятность постановки диагноза D 1 (исправное состояние), при реально существующем состоянии с диагнозом D 2 (неисправное состояние), что соответствует ошибочному пропуску определения состояния с диагнозом D 2. Вероятность такого события определяется вероятностью диагноза D 1 при наличии признака K, который определяет не нулевое значение вероятности P (D 2/ K). Подобным же образом находится вероятность ложной тревоги:
Следовательно, Р (H 21) показывает вероятность постановки диагноза D 2 (неисправное состояние), при реально существующем состоянии с диагнозом D 1 (исправное состояние), что соответствует ошибочному пропуску определения состояния с диагнозом D 1, т.е. мы приняли исправное состояние за неисправное, а это есть «ложная тревога». Вероятность такого события определяется вероятностью диагноза D 2 при наличии признака K, который определяет не нулевое значение вероятности P (D 1/ K). По результатам диагностического обследования ошибочное решение будет принято, если имеет место пропуск цели или ложное срабатывание. Таким образом, вероятность ошибочного решения по правилу сложения вероятностей равна
Эта вероятность часто называется также уровнем значимости ошибки диагностирования. Доверительная вероятность правильного решения при диагностировании определяется по формуле
как сумма вероятностей правильного определения каждого из диагнозов. Пример Задача. Из 1000 обследованных подшипников агрегата 900 подшипников выработали ресурс в исправном состоянии и 100 в неисправном. Все подшипники были обследованы по следующим параметрам: – среднее квадратическое значение (общий уровень) вибрации; – температура; – загрязнение смазки. У N 11=540 исправных подшипников (или 60%) среднее квадратическое значение вибрации лежало в диапазоне до 12 м/с2, у N 12=180 исправных подшипников (20%) вибрация была в пределах от 12 до 16 м/с2 и у N 13=180 (20%) – более 16 м/с2. У N 21=630 исправных подшипников (70%) температура лежала в диапазоне до 70 ºС, у N 22=135 (15%) – в диапазоне от 70 ºС до 90 ºС, и у N 23=135 (15%) – более 90ºС. У N 31=810 исправных подшипников (90%) загрязнение смазки было в пределах нормы. У L 13=80 неисправных подшипников (80%) наблюдалась вибрация более 16 м/с2, у L 12=10 неисправных подшипников (10%) вибрация в диапазоне от 12 до 16 м/с2. У L 23=85 неисправных подшипников (85%) температура была более 90 ºС, а у L 22=7 неисправных подшипников (7%) – в диапазоне от 70 ºС до 90 ºС. У L 32=80 неисправных подшипников (80%) загрязнение смазки было выше нормы. Пусть диагноз D 1 –исправное состояние; диагноз D 2 – неисправное состояние; признак k 1 – вибрация, его разряды: k 11 –до 12 м/с2; k 12 – от 12 до 16 м/с2; k 13 – более 16 м/с2; признак k 2 – температура, его разряды: k 21 – диапазон до 70 ºС; k 22 – диапазон от 70 до 90 ºС; k 23 – более 90 ºС; признак k 3 – загрязнение смазки, его разряды: k 31 – в пределах нормы; k 32 – выше нормы. Сведём исходные данные в таблицу 1.2. Таблица 1. 2 Исходные данные
Задание. 1. Рассчитать вероятность исправного и неисправного состояний подшипника при наблюдении вибрации в диапазоне до 12 м/с2 (k 11), температуры в диапазоне от 70 до 90 ºС (k 22), загрязнения смазки выше нормы (k 32). 2. Уточнить априорные вероятности появления исправного и неисправного состояний, а также условные вероятности признаков, если в результате обследования 1001-го подшипника установлено, что у него было исправное состояние и наблюдались: вибрация свыше 16 м/с2 (k 13), температура от 70 до 90 ºС (k 22), загрязнение смазки меньше нормы (k 31).
Решение. По условию поставленной задачи, общее число обследованных подшипников N =1000, число исправных N 1=900, число неисправных N 2=100. Следовательно:
В соответствии с исходными данными произведём расчёт (1.4) и составим диагностическую матрицу (табл. 1.2). Для признака вибрации при исправном состоянии:
Для признака температуры при исправном состоянии:
Для признака загрязнённости смазки при исправном состоянии:
Для признака вибрации при неисправном состоянии:
Для признака температуры при неисправном состоянии:
Для признака загрязнённости смазки при неисправном состоянии:
Следует заметить, что диагностическую матрицу (табл. 1.3) можно получить непосредственно и из исходных данных (табл. 1.2) Таблица 1. 3 Диагностическая матрица
Рассчитаем вероятность диагноза D 1 (исправное состояние) при выявлении комплекса признаков K* с реализациями k 11, k 22 и k 32:
Таким образом, вероятность исправного состояния при вибрации подшипника до 12 м/с2, температуре в диапазоне от 70 до 90 ºС, загрязнении смазки выше нормы, составляет приблизительно 0,93533 (93,533 %). Определим вероятность диагноза неисправного состояния (D 2) при выявлении комплекса признаков K* с реализациями k 11, k 22 и k 32:
Следовательно, вероятность неисправного состояния подшипника при его вибрации до 12 м/с2, температуре в диапазоне от 70 до 90 ºС, загрязнении смазки выше нормы, составляет приблизительно 0,06467 (6,467 %). Очевидно, что этот результат можно было получить и другим путём, учитывая, что исправное и неисправное состояния образуют полную группу событий: P (D 2/ K *) = 1 – P (D 1/ K *) = 1 – 0,93533 = 0,06467. Уточним априорные вероятности появления исправного и неисправного состояний, а также условные вероятности признаков по результатам обследования 1001-го подшипника (количество исправных подшипников N 1=901, неисправных N 2=100, всего подшипников N =1001, диагноз D 1; признаки k 13, k 22 и k 31). Уточнённая априорная вероятность исправного состояния (1.17):
Уточнённая априорная вероятность появления неисправного состояния
Произведём корректировку условных вероятностей разрядов признака согласно формуле (1.18): для первого разряда признака k 11:
для второго разряда признака k 12:
для третьего разряда признака k 13:
для первого разряда признака k 21
для второго разряда признака k 22
для третьего разряда признака k 23
для первого разряда признака k 31
для второго разряда признака k 32
По полученным данным составим уточнённую диагностическую матрицу (табл. 1.4) Таблица 1. 4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.241 (0.204 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
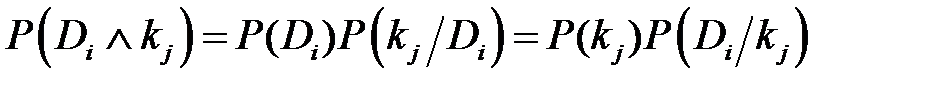 .
.
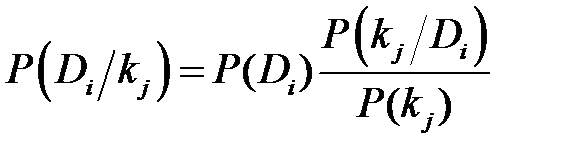 .
.
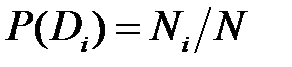 .
.
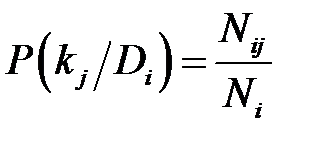 .
.
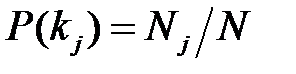 .
.
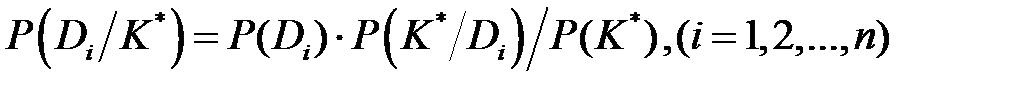 ,
,
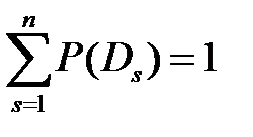 .
.
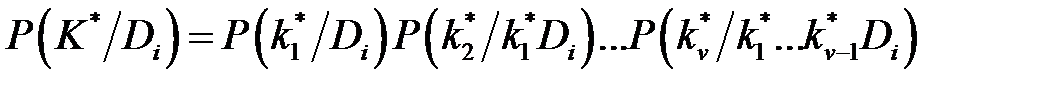 ,
,
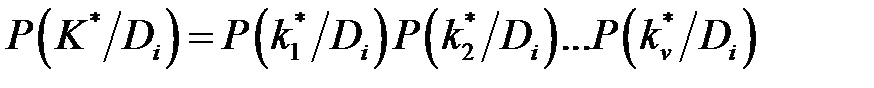 .
.
 .
.
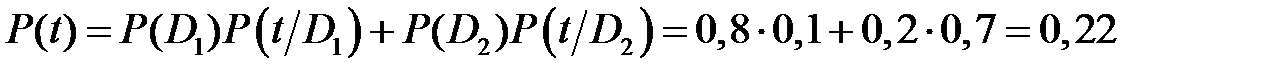 .
. ,
,
 ,
,
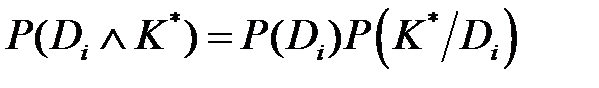 .
.
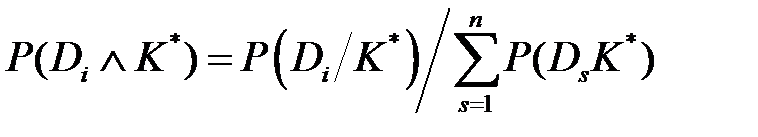 .
.
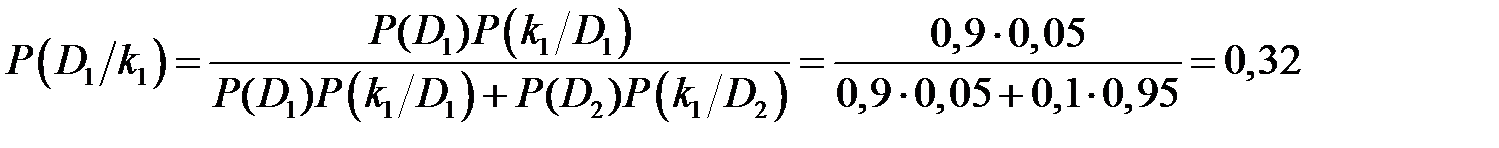 .
.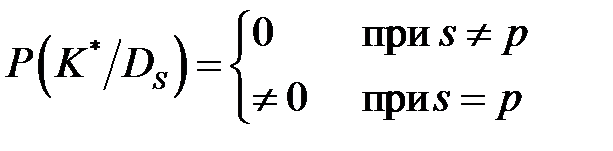 .
.
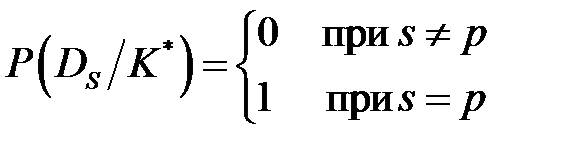 .
.
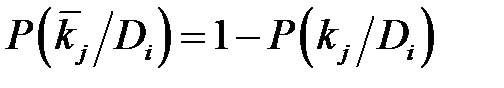 .
.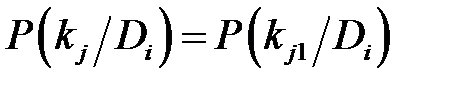
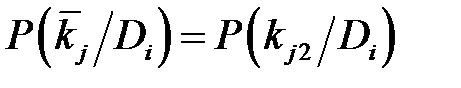 .
.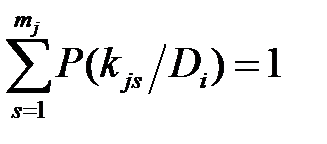 , где mj – число разрядов признака kj.
, где mj – число разрядов признака kj.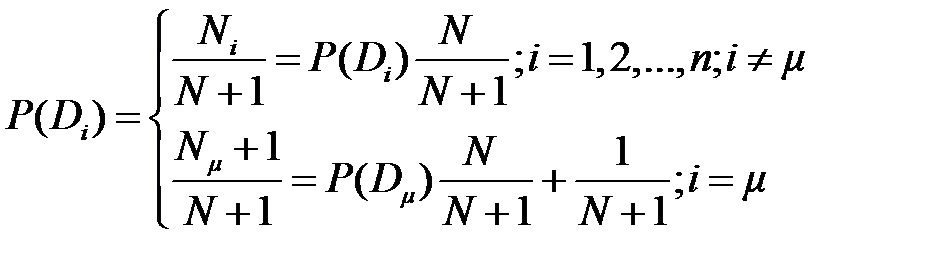 .
.
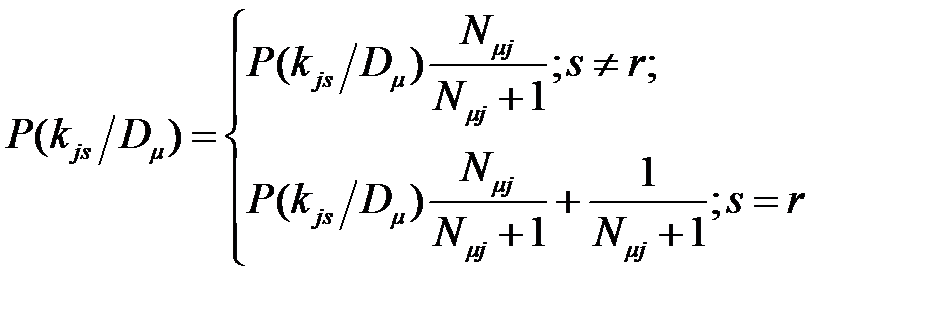 .
.
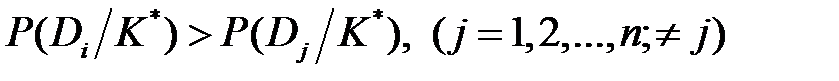 .
.
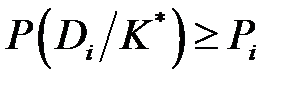 ,
,
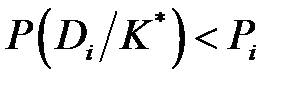 ,
,
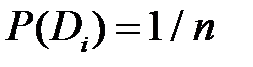 .
.
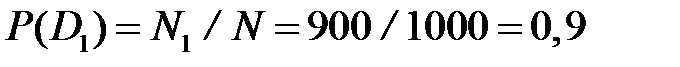 ,
,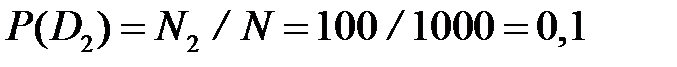 .
.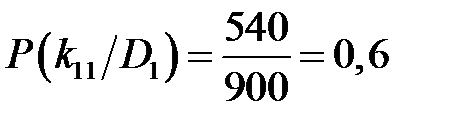 ;
; 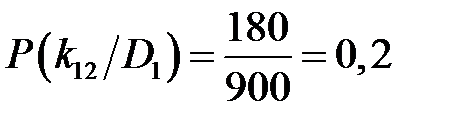 ;
;  .
. ;
;  ;
; 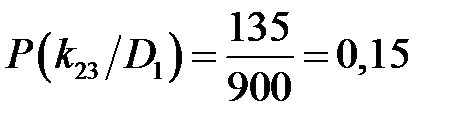 .
.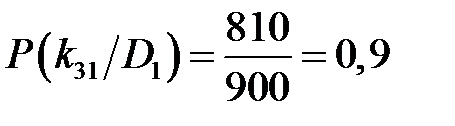 ;
;  .
.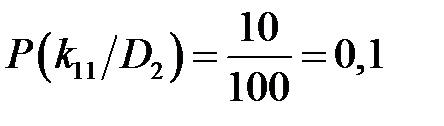 ;
; 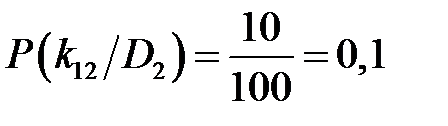 ;
; 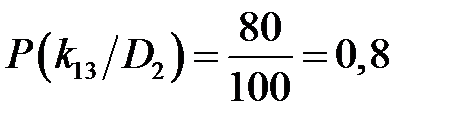 .
.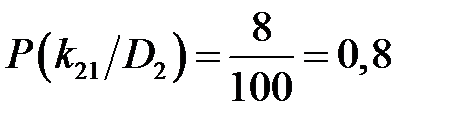 ;
; 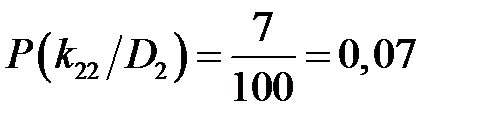 ;
; 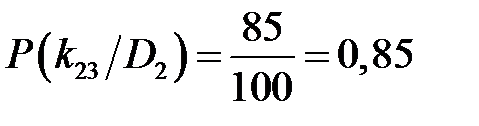 .
.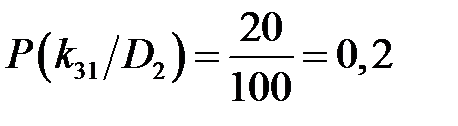 ;
; 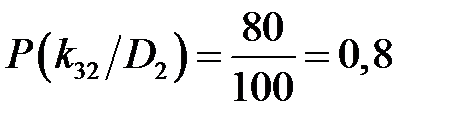 .
.

 .
. .
.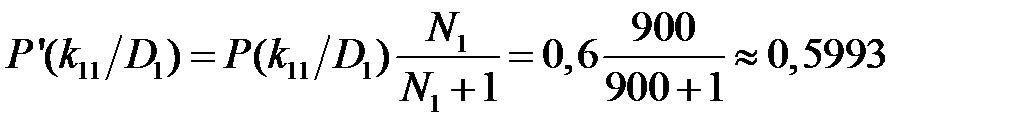 ,
, ,
,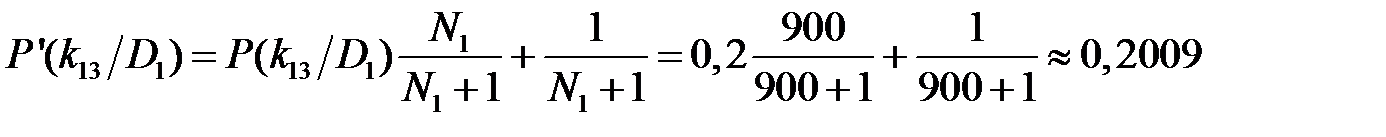 ,
,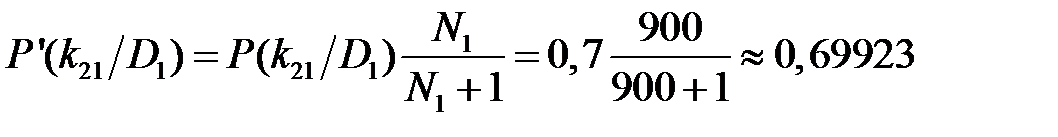 ,
,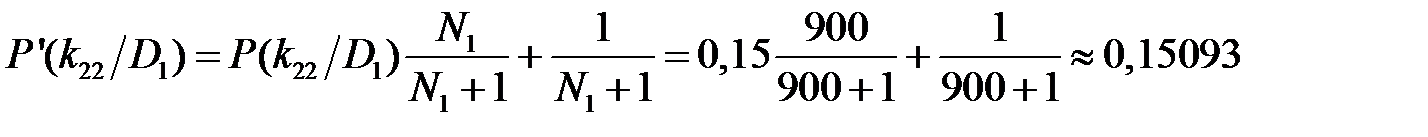 ,
,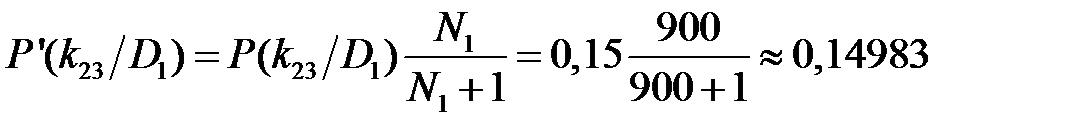 ,
,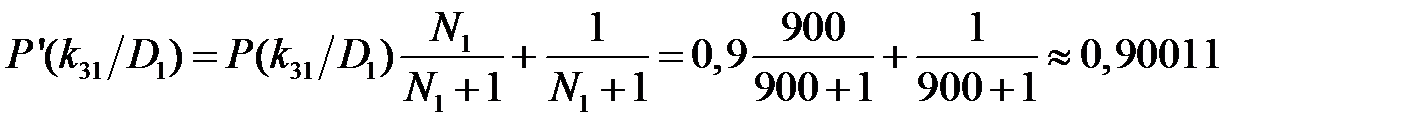 ,
,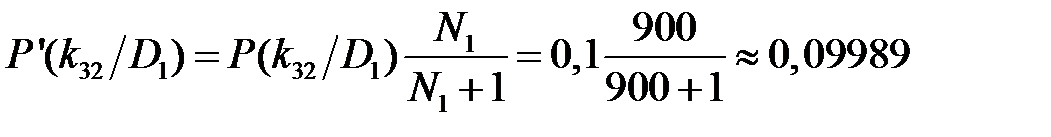 .
.


