Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь границ принятия решения с вероятностями ошибок первого и второго рода
Ошибка, относящаяся к диагнозу D 1 (принимается решение о наличии диагноза D 2, когда в действительности объект принадлежит диагнозу D 1), называется ошибкой первого рода. Ошибка, относящаяся к диагнозу D 2 (принимается решение в пользу диагноза D 1 когда справедлив диагноз D 2), называется ошибкой второго рода. Считая состояние D 1 исправным, а состояние D 2 дефектным, легко понять, что ошибка первого рода является «ложной тревогой», а ошибка второго рода «пропуском дефекта» или «пропуском цели». Обозначим вероятность ошибки первого рода α, второго рода β. Допустим, что имеются условия и принимается решение в пользу диагноза D 2. Вероятность того, что это решение будет справедливым, равна (1- β). Вероятность принадлежности объекта с данной реализацией признаков к диагнозу D 1 составляет α. С другой стороны, в силу соотношения (2.10) вероятность диагноза D 2, по крайней мере, в А раз больше, чем диагноза D 1 т.е.
Подобным образом можно получить и следующую оценку:
Таким образом, границы рассчитывают, исходя из вероятностей ошибок первого α и второго β рода, которые считаются заданными. В практических расчётах можно принимать α=β= 0,05 … 0,1. Для упрощения вычислений отношений правдоподобия формулы (2.12), (2.13) представляют в виде логарифмов отношений (2.5), (2.6), (2.7) и тогда условия принятия гипотез записывают следующим образом: принятие гипотезы H 1
отклонение гипотезы H 0
Условие продолжения испытаний:
Пример Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение x 0подшипникового узла составляет В результате измерений получены следующие данные: х 1=75 оC, х 2=70°C, х 3=75°C, х 4=80°C, х 5=75°C, х 6=80°C, х 7=85°C. Примем α=β= 0,05. Решение. Определим границы принятия решений:
Критерий правдоподобия для нормального закона распределения одного измерения получаем из соотношения:
И затем после каждого n -ого измерения вычисляем логарифм отношения:
Если логарифм отношения L лежит в пределах
В результате расчётов получим следующие данные: L 1=–0,454; L 2=–0,54; L 3=–0,994; L 4=–1,583; L 5=–2,307; L 6=–3,165; L 7=–4,463 и представим их на рис. 2.1. Таким образом, на шестом шаге превышена нижняя граница («изделие не принимают»), что означает – для постановки диагноза «температура превышена» достаточно шести измерений.
Рис. 2.1. Пересечение нижней границы при проведении последовательного анализа – изделие не принято на шестом измерении
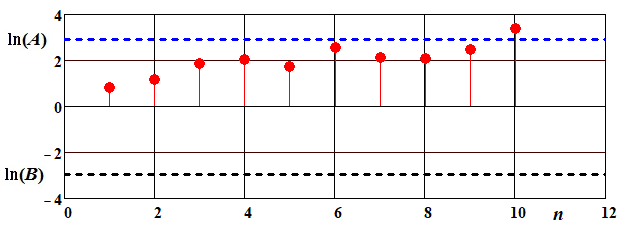
Предположим, что в результате измерений получены следующие данные: х 1=54оC, х 2=64°C, х 3=57°C, х 4=66°C, х 5=73°C, х 6=54°C, х 7=75°C, х 8=69°C, х 9=63°C, х 10=52°C. Примем α=β= 0,05. В результате расчётов получены следующие данные: L 1=0,847; L 2=1,154; L 3=1,854; L 4=2,035; L 5=1,733; L 6=2,579; L 7=2,125; L 8=2,108; L 9=2,476; L 10=3,413 и представим их на рис. 2.2.
Рис. 2.2. Пересечение верхней границы при проведении последовательного анализа – изделие принято на десятом измерении
На десятом шаге измерений превышена верхняя граница («изделие принимают»), что означает – для постановки диагноза «температура не превышена» достаточно десяти измерений. Следует заметить, что в данном случае разброс измеренных величин температуры достаточно велик. Контрольные вопросы 1. Дайте определение методу последовательного анализа. 2. Поясните критерий отношения правдоподобия. 3. В чем состоит связь границ принятия решения с вероятностями ошибок первого и второго рода? 4. Поясните понятие «нулевая гипотеза». 5. Поясните понятие «конкурирующая гипотеза». 6. Что такое «риск поставщика»? 7. Поясните понятие «риск заказчика». Задания для практических работ Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение x 0подшипникового узла составляет В результате измерений получены данные, приведённые в табл. 2.1. Выбирая из массива последовательно точки измерений, необходимо определить номер измерения, после которого будет превышен порог.
Содержание отчёта 1. Название расчёта, задача и номер варианта; 2. Расчётные формулы с пояснительным текстом; 3. Расчётные формулы с численными значениями; 4. Выводы по работе. Таблица 2.1 Исходные данные для задачи
3 Объем испытаний методом Средний объем испытаний методом последовательного анализа для различных законов распределения наработки на отказ при справедливости гипотезы H 0 выражается соотношением [6, 10, 13, 14, 15]
где Соответственно при справедливости гипотезы H 1 средний объем испытаний равен:
В [6, с. 127, 13, с. 377] приведены формулы для определения границ приёмки и отбраковки:
При каждом m – число текущих испытаний, правая часть неравенства (3.4) обозначена через mПР и называется приёмочным числом или границей приёмки. Аналогично правая часть (3.3) обозначена mБР и называется браковочным числом или границей браковки [14, с. 201] Планирование испытаний для нормального закона Одной из задач надёжности является планирование испытаний методом последовательного анализа при двух заданных уровнях показателя надёжности для нормального закона распределения наработки на отказ [11, 14, 15]. В этом случае средний объем испытаний методом последовательного анализа c двухсторонней доверительной границей для подтверждения наработки на отказ T 0, подчинённой нормальному закону, в интервале T 1 ≤ T ≤ T 0 определяют из соотношения:
где При планировании испытаний восстанавливаемых изделий обычно предполагают, что ошибка первого рода (т.е. риск поставщика или ложная тревога) равна нулю (α= 0), тогда выражение (4.1) преобразуется к виду:
Для подтверждения наработки на отказ T 1 средний объем испытаний находится по формуле
Найдём математическое ожидание логарифма отношения значений функций плотности распределения f (t, T, σ) наработки на отказ при T = T 1 и T = T 0.
Математическое ожидание логарифма отношения правдоподобия при условии σ 1= σ 2= σ и плотности распределения, представленного нормальным законом
в виде
можно записать в следующем виде
Выражение (4.6) получено в предположении, что, преобразуя (4.5), получим соотношение
которое можно записать в виде
если принять допущение, что каждый период испытаний по времени одинаков, т.е. ti = t. Подставляя полученное выражение в формулу (4.2), можно определить выражение для среднего объёма испытаний, если риск поставщика равен нулю:
В общем случае средний объем испытаний для подтверждения средней наработки на отказ T 0 получим, подставляя (4.6) в (4.1):
где n 0 – число периодов работы длительностью T 0 каждый или число отказов за время S испытаний, которое равно:
Средний объем испытаний для подтверждения средней наработки на отказ T 1 можно определить по формуле:
На основании выражения (4.8) для логарифма отношения правдоподобия можно записать условия принятия и отклонения гипотезы H 0 состоящей в том, что при превышении в текущем испытании T = T 0: отклонение гипотезы H 0
принятие гипотезы H 1
Так как в процессе испытаний фиксируют число отказов m, то условия принятия и отклонения гипотезы H 0 можно представить в виде неравенств:
Пример Задача. Построить линию приёмки и линию браковки для нормального закона распределения наработки на отказ при следующих исходных данных: T 0= 100 ч; σ =10 ч; α = β =0,1 [11, 14]. Определить уравнения линий приёмки и браковки, построить их графики, найти средний объем испытаний. Решение. Для построения линий приёмки mПР и браковки mБР (рис. 4.1) воспользуемся формулами (4.15) и (4.16) при некоторых значениях T 0/ T 1.
Рис. 4.1. Графики линий приёмки (––) и браковки (- - -) для нормального закона при T 0= 100 ч; σ =10 ч; α = β =0,1
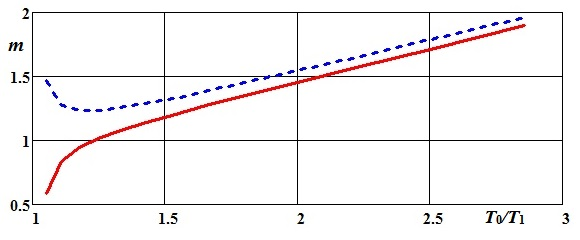
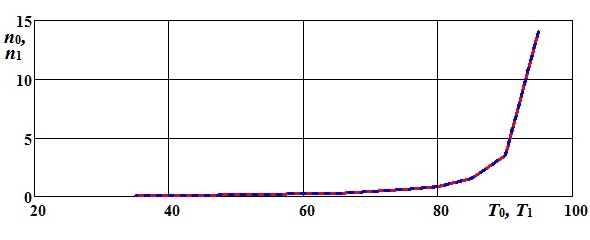
Средний объем испытаний для подтверждения средней наработки на отказ T 0 оценим количеством испытаний по формуле (4.10) (рис. 4. 2)
Для подтверждения наработки на отказ T 1 средний объем испытаний оценим количеством испытаний по формуле (4.12) (рис. 4.2).
Рис. 4.2. Зависимость количества циклов испытаний от текущей наработки на отказ T 1 Контрольные вопросы 1. Поясните процедуру получения математического ожидания случайной величины из последовательности наблюдений M, при которых параметр T принимает значение T 0 или T 1.
2. Поясните вывод формулы для математического ожидания случайной величины при одинаковых величинах дисперсии. 3. Поясните вывод формулы для математического ожидания случайной величины при различных величинах дисперсии.
Задания для практических работ Построить линии приёмки и браковки, принимая во внимание, что вероятность отказа подчиняется нормальному закону для исходных данных в табл. 4.1 (n 0 рассчитано для контроля при T 1=0,95 T 0) и определить среднее число испытаний (n 0, n 1). Содержание отчёта 1. Название расчёта, задача и номер варианта; 2. Расчётные формулы с пояснительным текстом; 3. Расчётные формулы с численными значениями; 4. Выводы по работе.
Таблица 4.1 Исходные данные для нормального закона
Планирование испытаний для биномиального закона В случае биномиального закона распределения для n независимых испытаний с вероятностью отказа q и вероятностью наработки требуемого ресурса p в каждом из них, вероятность появления m отказов определяется по формуле [11, 14]:
и при двух заданных уровнях показателя надёжности объем испытаний или число отказов определяют путём решения уравнения правдоподобия при заданных значениях вероятности ложной тревоги (риска поставщика) α и пропуска цели (риска заказчика) β, а также из отношения q 1/ q 0:
Согласно соотношениям (2.12)…(2.16) испытания продолжают до тех пор, пока не выполнится неравенство
Испытания следует прекратить и принять гипотезу H 0, т.е. вероятность отказа соответствует величине q 0, если
или принять гипотезу H 1, т.е. вероятность отказа соответствует величине q 1, если
Поскольку в процессе испытаний фиксируют число отказов m, то условия принятия и отклонения гипотез H 0 и H 1 можно представить в виде неравенств [6, с. 127] и принять гипотезу H 0, если
или принять гипотезу H 1, если
где mПР и mБР – соответственно приёмочное и браковочное число отказов. По полученным формулам и для заданной вероятности безотказной работы P 0=1– q 0 и минимально допустимому значению этой вероятности P 1=1– q 1, а также для заданных значений α и β находят уравнения соответствия и несоответствия изделия заданным требованиям.
Средний объем испытаний, который необходим для подтверждения отказа q = q 0, можно оценить по формуле:
Для подтверждения отказа q = q 1 средний объем испытаний можно оценить по формуле:
Пример Задача. В техническом задании на изделие указана вероятность безотказной работы P 0(t) = 0,9; допустимое значение этой величины равно P 1(t) = 0,8. Заданные требования по надёжности должны подтверждаться с уровнем риска поставщика α и заказчика β, равными: α = β =0,1 [11, 14, 15]. Определить уравнения линий приёмки и браковки, построить их графики, найти средний объем испытаний для биноминального закона. Решение. Для построения линий приёмки и браковки из (5.6) и (5.7) получим условие принятия гипотезы H 0:
условие принятия гипотезы H 1:
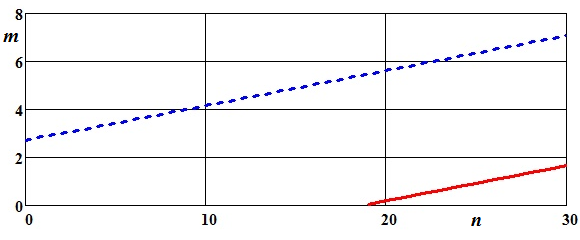
По полученным выражениям можно построить линии приёмки и отбраковки (рис. 5.1). Рис. 5.1
Рис. 5.1. Графики линий приёмки (––) и браковки (- - -) для биномиального закона при P 0(t) = 0,9; P 1(t) = 0,8; α = β =0,1. Для определения среднего объёма испытаний воспользуемся формулами (5.8) и (5.9):
Контрольные вопросы 1. Поясните, как соотносятся между собой вероятности ложной тревоги (риска поставщика) α и пропуска цели (риска заказчика) β. 2. Поясните, при каких условиях принимают гипотезу H 0. 3. Поясните, при каких условиях принимают гипотезу H 1. Задания для практических работ Построить линии приёмки и браковки, принимая во внимание, что вероятность отказа подчиняется биномиальному закону для исходных данных в табл. 5.1 и определить среднее число испытаний (n 0, n 1). Таблица 5.1 Содержание отчёта 1. Название расчёта, задача и номер варианта; 2. Расчётные формулы с пояснительным текстом; 3. Расчётные формулы с численными значениями; 4. Выводы по работе. Таблица 5.1 Исходные данные для биномиального закона
Планирование испытаний для экспоненциального закона Экспоненциальный закон распределения времени безотказной работы или функция надёжности определяется формулой:
Здесь λ – интенсивность отказов (параметр распределения), T = 1/ λ – средняя наработка на отказ. Если принять, что λ<<0,1, то формула вероятности безотказной работы упрощается в результате разложения в ряд и принимает вид:
Плотность распределения экспоненциального закона описывается выражением
а функция распределения – зависимостью вида
Используя логарифм (2.1), можно получить [11, 14]
Принимая ti = t, после логарифмирования правой части этого выражения можно получить:
Согласно соотношениям (2.12)…(2.16) для принятия или отклонения гипотезы H 0 в зависимости от полученного числа отказов m можно получить следующие условия принятия гипотезы H 0:
отклонения гипотезы H 0:
где S = nt – общая продолжительность испытаний до наступления m -го отказа; среднее ожидаемое число отказов m и среднее ожидаемое время испытаний S в зависимости от величин T 0/ T 1, α и β следует определять по приведённым ниже формулам. Так, для подтверждения того, что T = T 0, используют следующие формулы:
откуда общая продолжительность испытаний
Для подтверждения выполнения условий T = T 1 проводят следующие расчёты:
откуда общая продолжительность испытаний
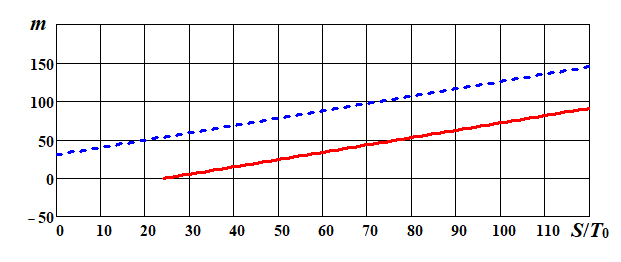
Пример Задача. Изделие должно обладать наработкой на отказ T 0 с рисками поставщика и заказчика α = β =0,1, при этом задано отношение T 0/ T 1 = 1,2. Требуется построить линии приёмки и браковки изделия по результатам испытаний [11, 14] и определить среднее число испытаний (m 0, m 1). Решение. Для вывода формул линий приёмки и браковки воспользуемся уравнениями (6.7) и (6.8) принятия и отклонения гипотезы H 0 (рис. 6.1): Рис. 6.1
Задаваясь значениями S / T 0, определим mПР и mБР для уровней соответствия и несоответствия изделия этим требованиям.
Рис. 6.1. Графики линий приёмки (––) и браковки (- - -) для экспоненциального закона при α = β =0,1; T 0/ T 1 = 1,2; m 0 = 99. Контрольные вопросы 1. Дайте определение экспоненциальному закону. 2. Поясните отношение правдоподобия для экспоненциального закона. 3. Поясните понятие «средняя наработка на отказ». Задания для практических работ Построить линии приёмки и браковки, принимая во внимание, что вероятность отказа подчиняется экспоненциальному закону для исходных данных в табл. 6.1. Величина m 0 приведена для контроля правильности расчётов. Таблица 6.1. Содержание отчёта 1. Название расчёта, задача и номер варианта; 2. Расчётные формулы с пояснительным текстом; 3. Расчётные формулы с численными значениями; 4. Выводы по работе. Таблица 6.1 Исходные данные для экспоненциального закона
7 Планирование испытаний Во многих задачах практики часто приходится встречаться со случайными величинами, которые в процессе испытаний принимают целые неотрицательные числа 0, 1, 2, …, m, причём последовательность этих чисел теоретически неограниченна. Случайная величина X распределена по закону Пуассона, если вероятность того, что она примет определённое значение m, выражается формулой [11, 14]
где a – некоторая положительная величина, называемая параметром закона Пуассона, является как математическим ожиданием, так и дисперсией закона. Это свойство распределения Пуассона частот применяют на практике для решения вопроса: правдоподобна ли гипотеза о том, что случайная величина X распределена по закону Пуассона. Рассмотрим один пример использования распределения Пуассона. Пусть в ремонтную мастерскую поступают заявки со средней плотностью 5 штук в течение рабочей смены за 10 ч. Считая, что число заявок на любом отрезке времени распределено по закону Пуассона, найти вероятность того, что за 2 ч рабочей смены поступит 2 заявки. Решение задачи сводится к следующему. Определяем среднее число заявок за 2 часа: а =2·5/10=1. Применяя формулу (7.1), найдём вероятность поступления двух заявок:
Таким образом, с вероятностью 0,184 за 2 часа работы поступит 2 заявки. Планирование испытаний методом последовательного анализа для закона Пуассона при двух заданных уровнях показателя надёжности осуществляют путём использования соотношений, выведенных исходя из записанного для этого закона логарифма отношения правдоподобия [13] (при a = q)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.2.122 (0.263 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
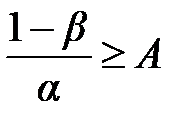 .
.
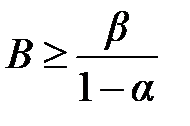 .
.
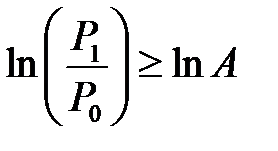 ;
;
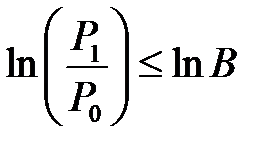 .
.
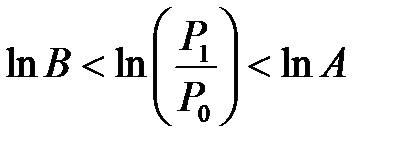 .
.
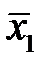 =50°C и среднее квадратичное отклонение σ 1=15°C. При наличии повышенного износа, где
=50°C и среднее квадратичное отклонение σ 1=15°C. При наличии повышенного износа, где  =100°C, σ 2=25°C, распределения предполагаются нормальными. Оценить объём испытаний.
=100°C, σ 2=25°C, распределения предполагаются нормальными. Оценить объём испытаний.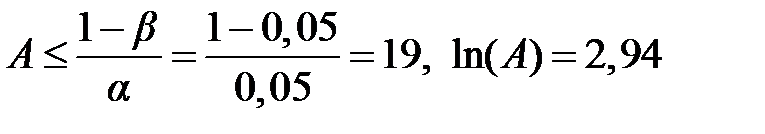 ,
,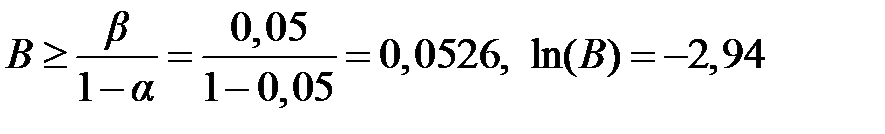 .
.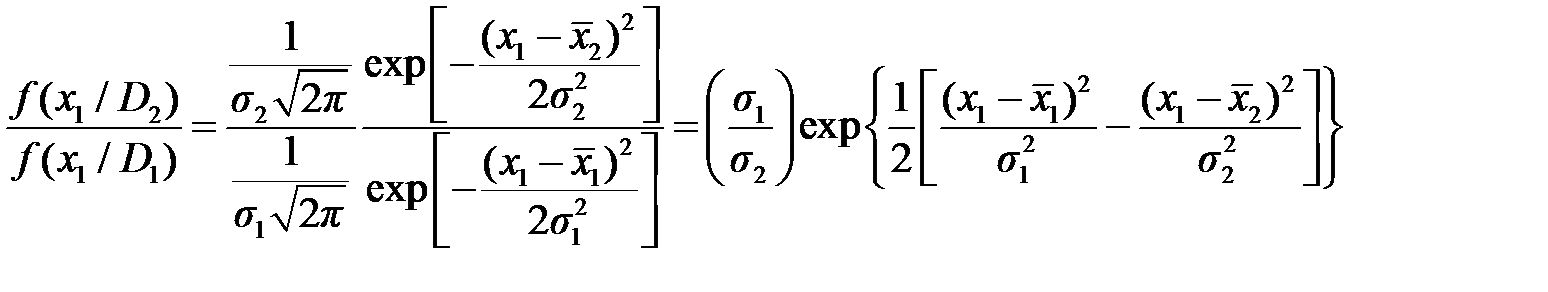 .
.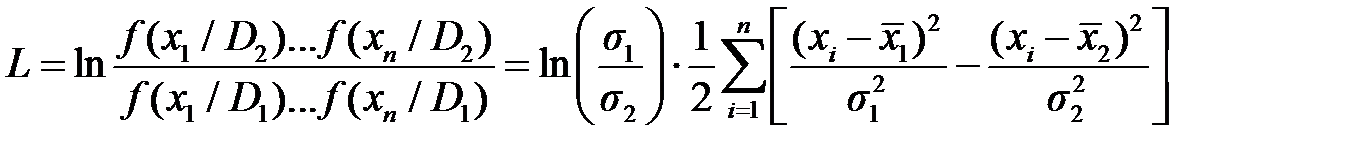 .
.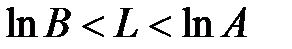 , то для постановки диагноза информации не хватает.
, то для постановки диагноза информации не хватает.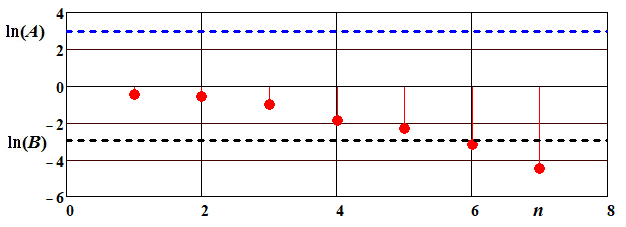
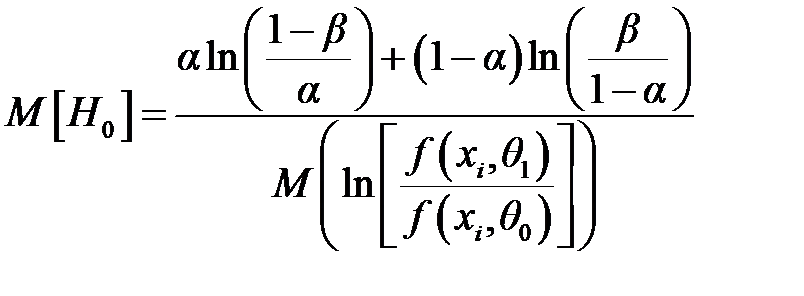 ;
;
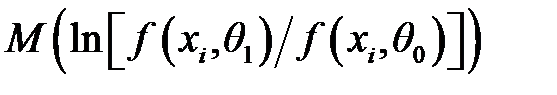 – математическое ожидание случайной величины из последовательности наблюдений, при которых параметр θ принимает значение θ 0.
– математическое ожидание случайной величины из последовательности наблюдений, при которых параметр θ принимает значение θ 0.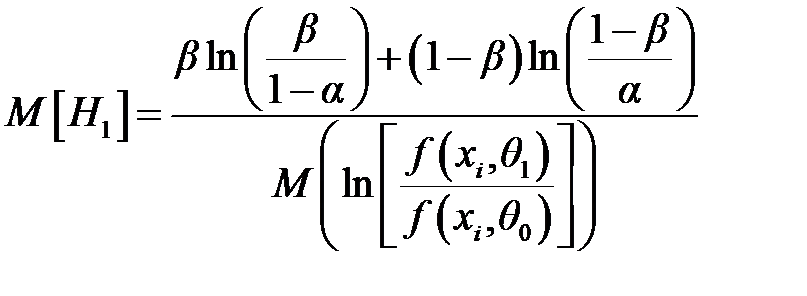 .
.
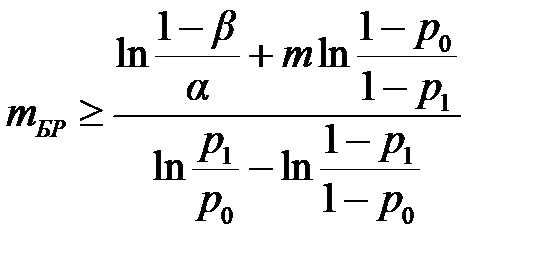 ;
;
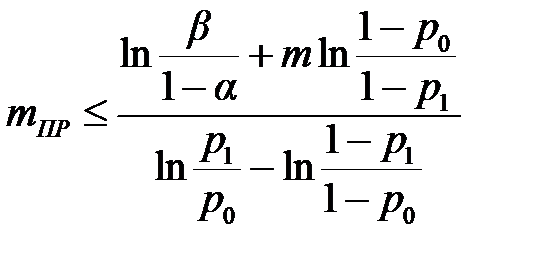 .
.
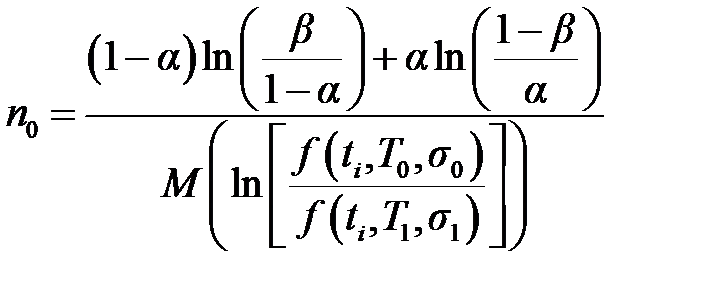 ;
;
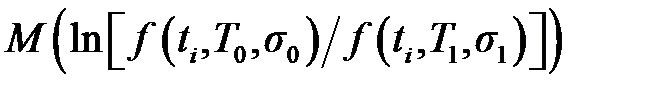 – математическое ожидание случайной величины из последовательности наблюдений M, при которых параметр T принимает значение T 0 или T 1.
– математическое ожидание случайной величины из последовательности наблюдений M, при которых параметр T принимает значение T 0 или T 1. .
.
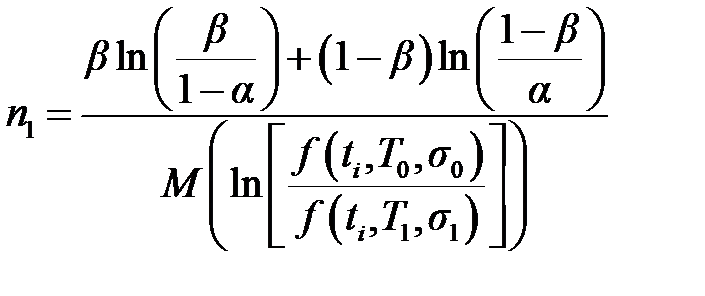 .
.
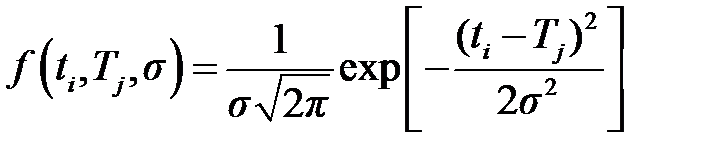 ,
,
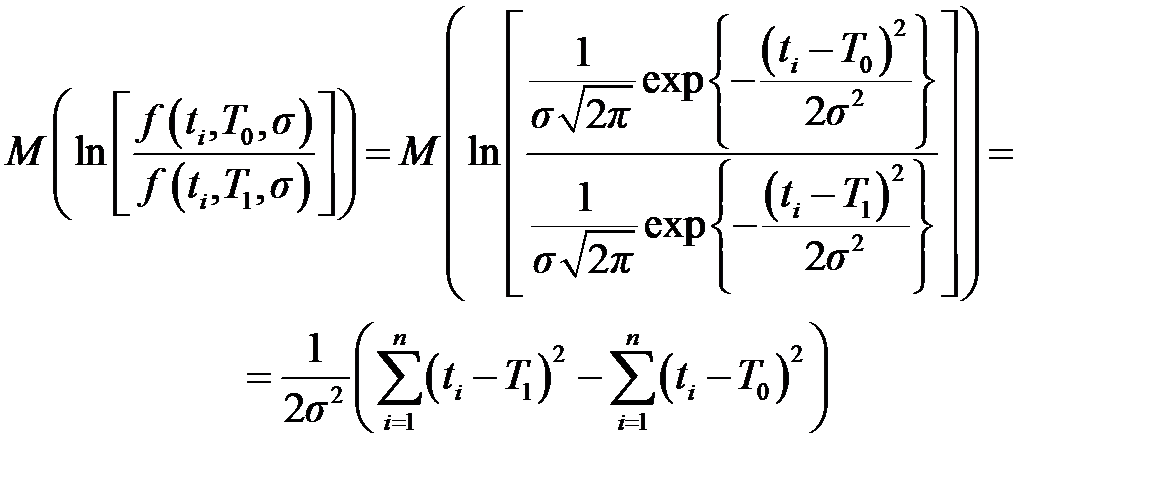
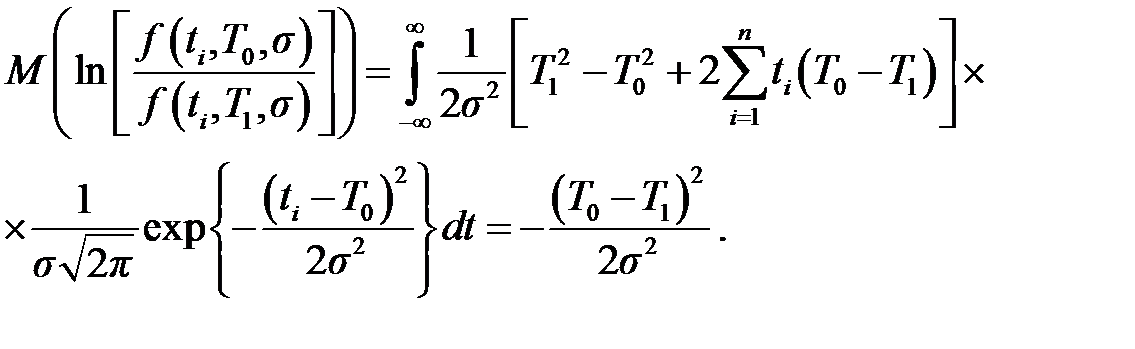
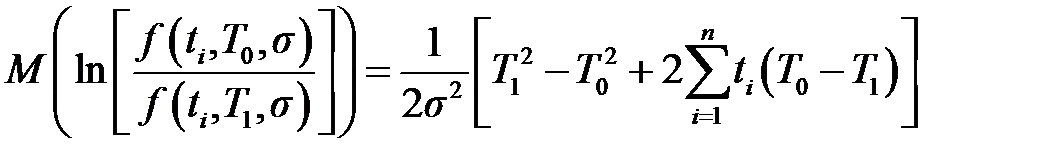 ,
,
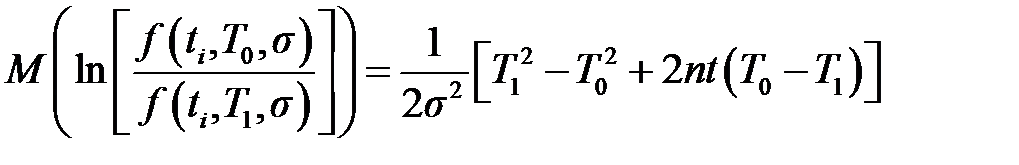 ,
,
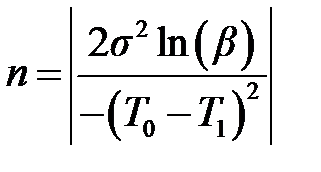 .
.
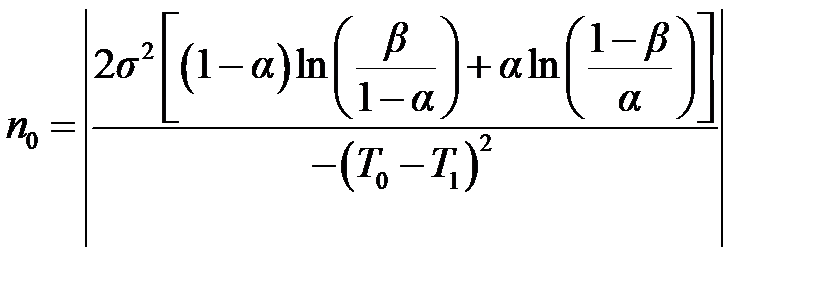 ,
,
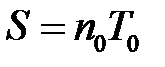 ;
;
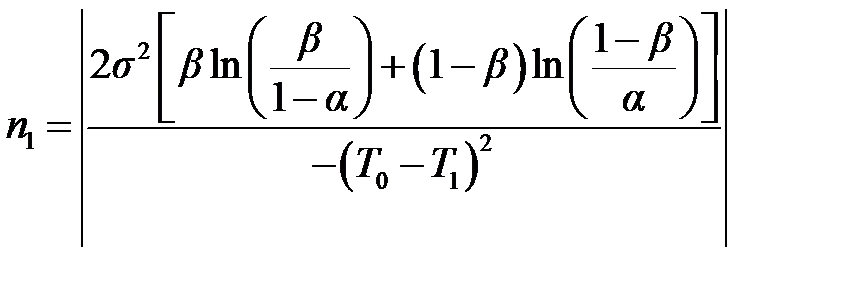 .
.
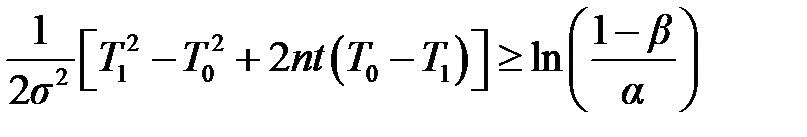 ;
;
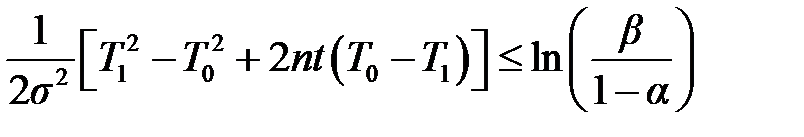 .
.
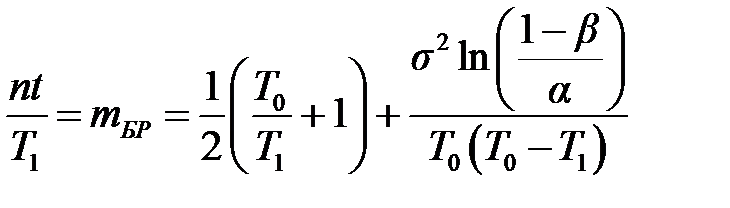 ;
;
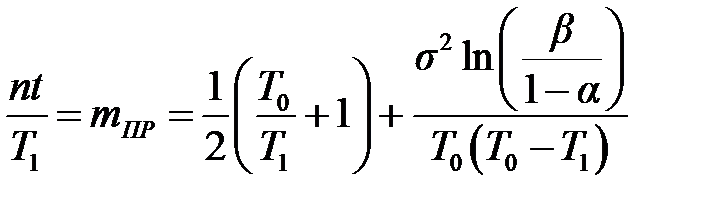 ;
;
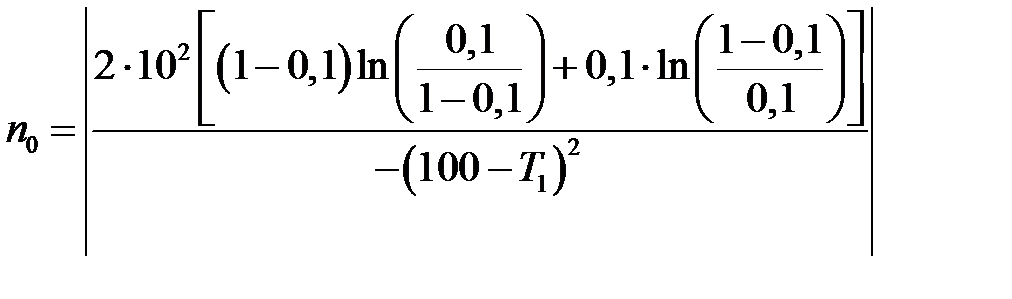
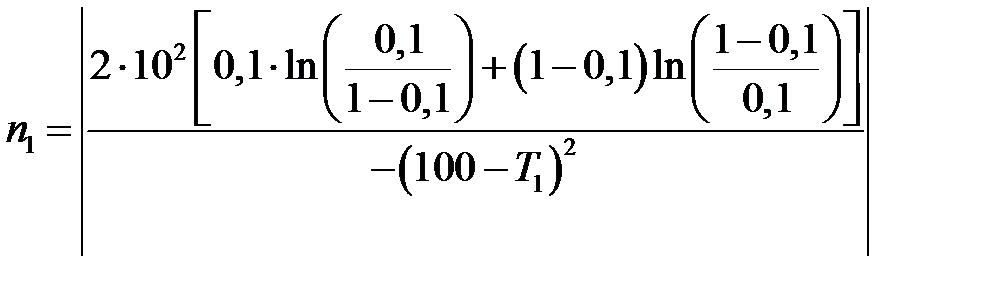
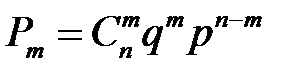 , где
, где 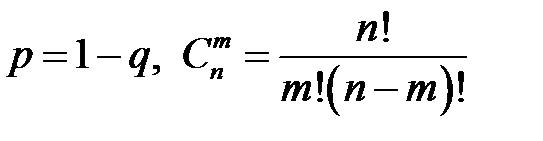
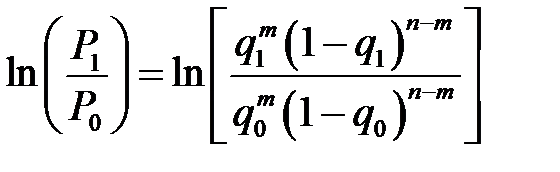 .
.
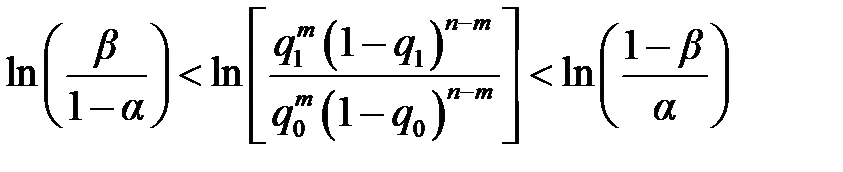 .
.
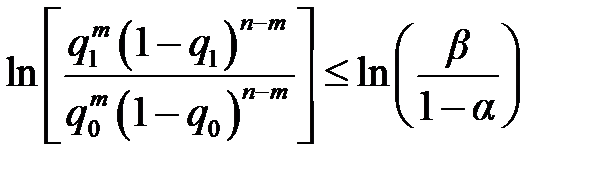 ,
,
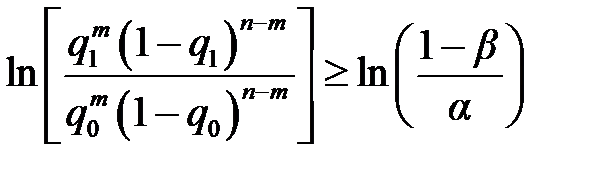 .
.
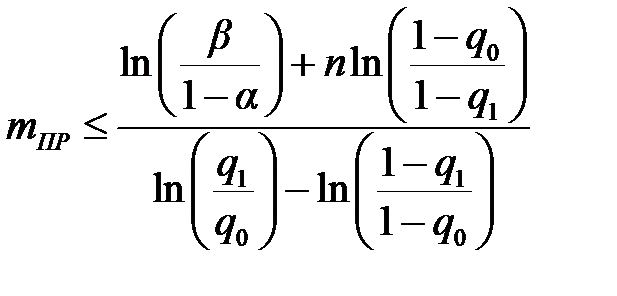
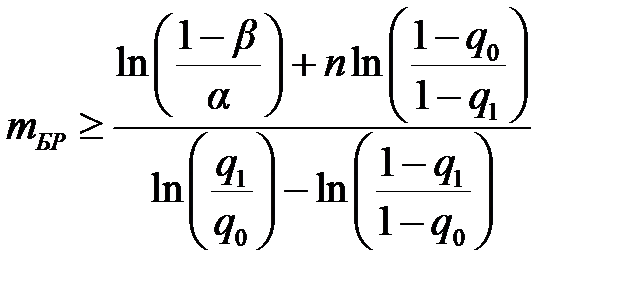 ,
,
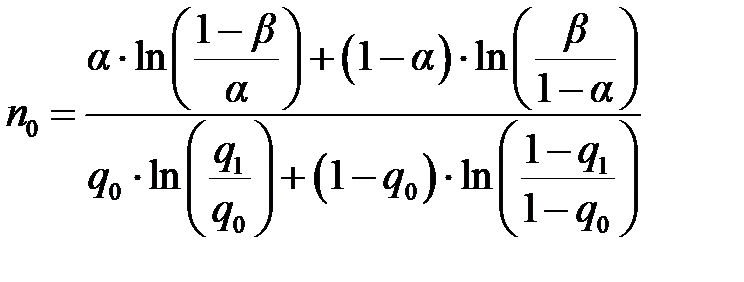 .
.
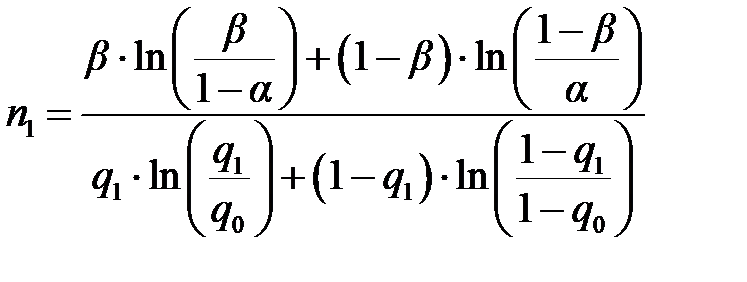 ;
;
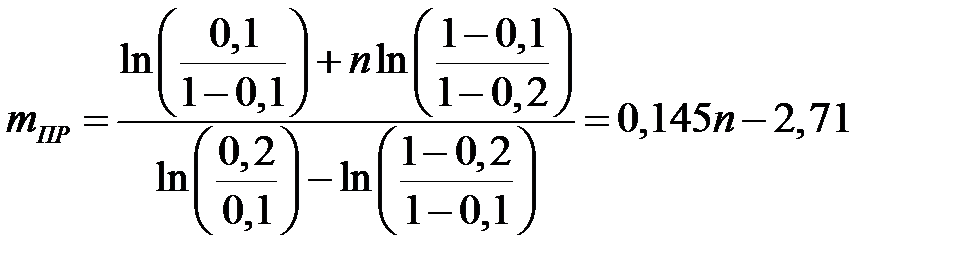 ;
;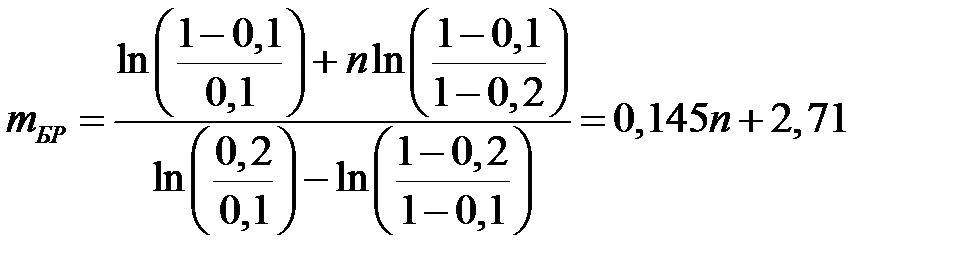 .
.
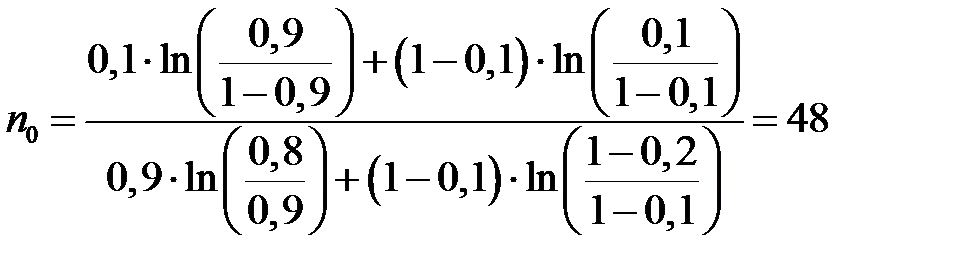 ;
;
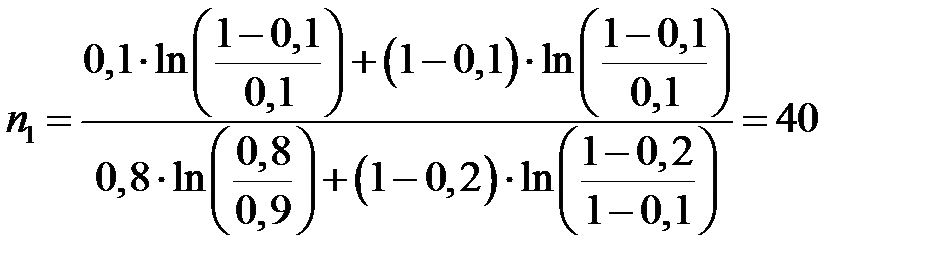 .
.
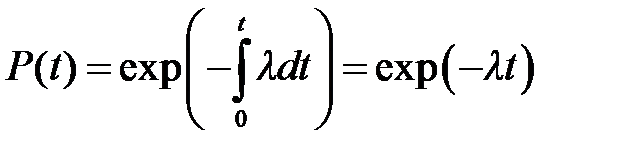 .
.
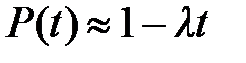 .
.
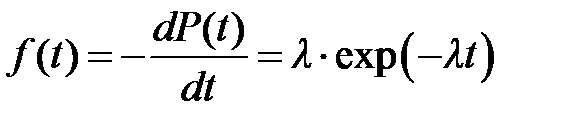 ,
,
 .
.
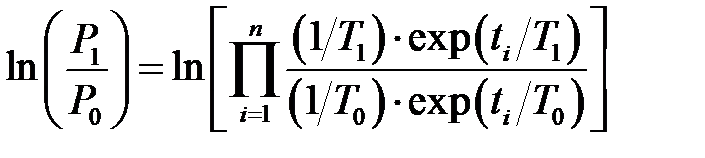 .
.
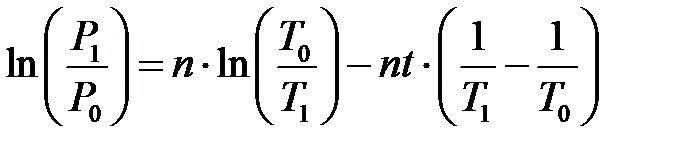 .
.
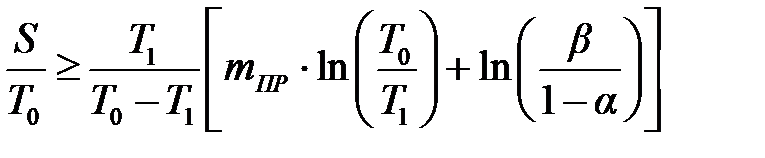 ;
;
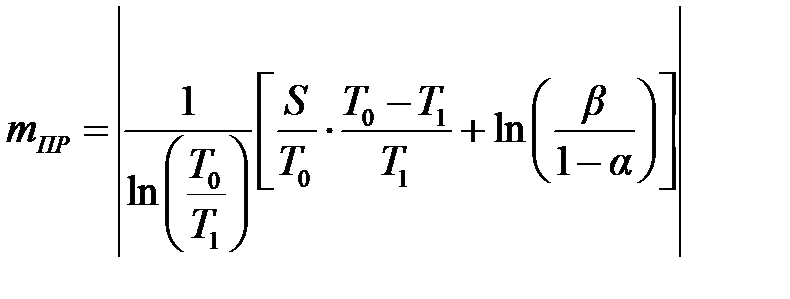 ;
;
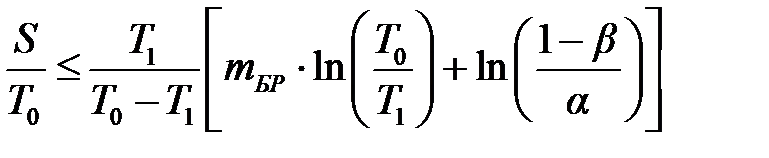 ;
;
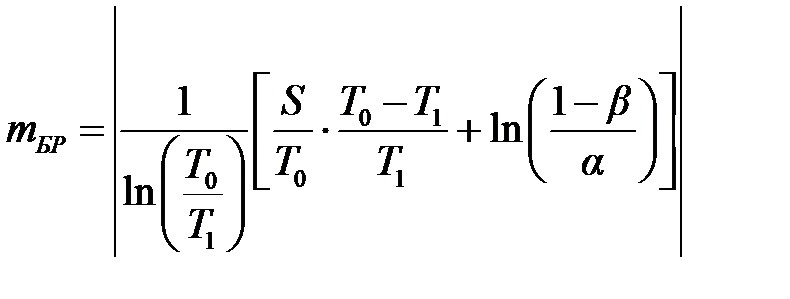 ,
,
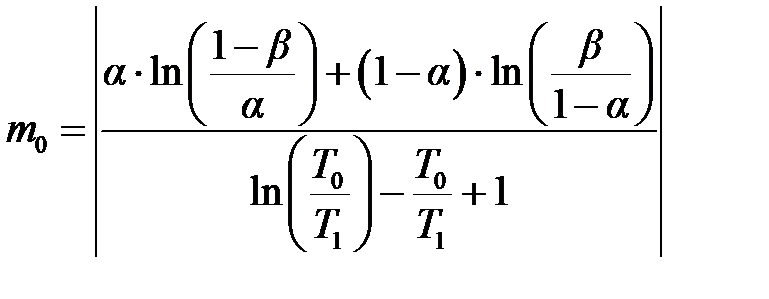 ,
,
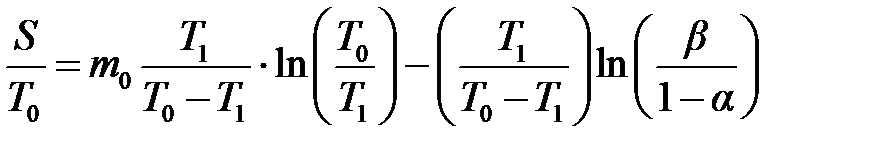 ,
,
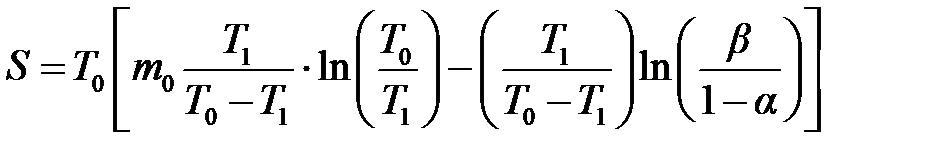 .
.
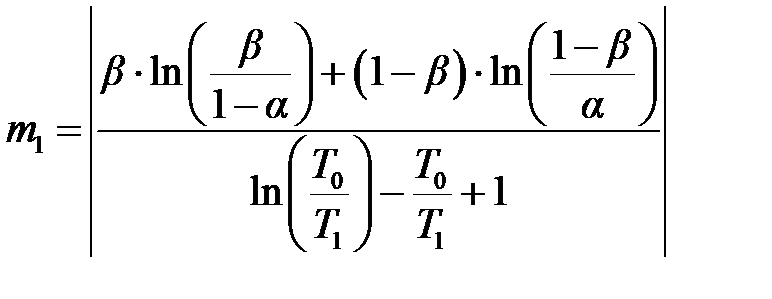 ,
,
 ,
,
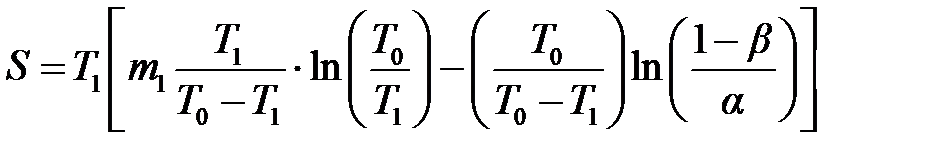 .
.
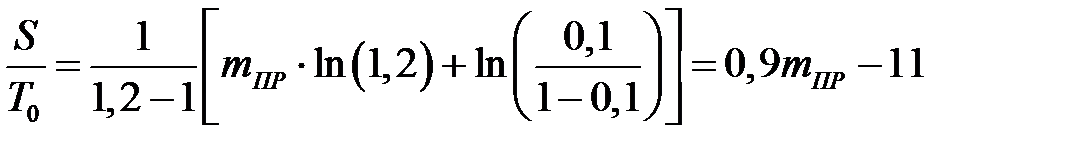 ;
; 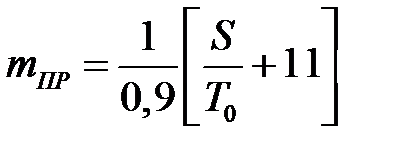 ;
;
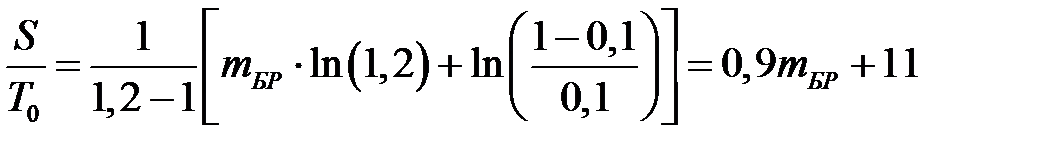 ;
; 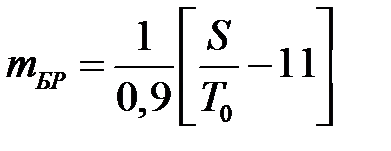 .
.
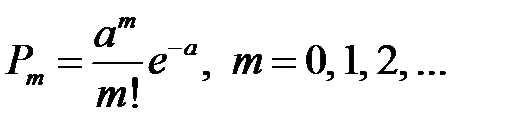 ,
,