
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смешанное произведение векторов. ⇐ ПредыдущаяСтр 8 из 8
О4. Смешанным произведением векторов Получим формулу для вычисления смешанного произведения
Обменяв местами первую строку со второй, а затем и с третьей, получим окон-чательную формулу 1. 2. Смешанное произведение векторов
Рис. 14. Объем параллелепипеда, построенного на векторах Так как
3. Если вектора Свойство 3 определяет условие компланарности трех векторов, т.е если Пример 4. Доказать, что вектора Согласно формуле, определяющей смешанное произведение векторов, имеем
Пример 5. Даны четыре точки Составим вектора
Положительность вычисленного объема указывает на то, что вектора Самостоятельная работа № 2 Основы векторной алгебры Даны четыре точки 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12)
13) 14) 15) 16) 17)
18) 19) 20) 21) 22) 23) 24) 1. Найти вектора 2. Найти единичный вектор того же направления что и вектор 3. Найти направляющие косинусы вектора 4. Найти 5. Определить координаты вектора 6. Вычислить скалярные произведения 7. Найти работу, совершенную материальной точкой, к которой приложена сила 8. Найти внутренний угол при вершине 9. Найти 10. Вычислить 11. Найти площадь 12. Найти единичный вектор, перпендикулярный векторам 13. Найти величину и направляющие косинусы момента силы 14. Лежат ли вектора 15. Чему равен объем пирамиды с вершинами 16. Вычислить 17. Вычислить 18. Найти вектор 19. Найти вектор
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.183.221 (0.026 с.) |
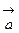 ,
, 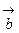 и
и  называется число равное векторному произведению
называется число равное векторному произведению 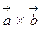 , умноженному скалярно на вектор
, умноженному скалярно на вектор 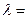
 .
.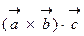
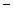
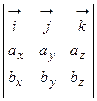 .
. 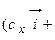

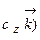
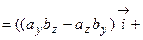
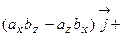
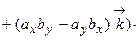

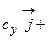
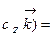
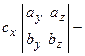
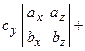
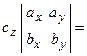
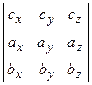
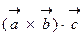
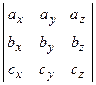 . Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
. Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства: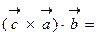
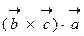 , т.е. вектора, входящие в смешанное произведение, можно циклически переставлять местами, поэтому зачастую смешанное произведение пишут без знаков
, т.е. вектора, входящие в смешанное произведение, можно циклически переставлять местами, поэтому зачастую смешанное произведение пишут без знаков 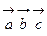 .
.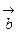 и
и 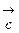 равно объему параллелепипеда, построенного на этих векторах, взятого со знаком «+», если тройка векторов правая, и со знаком «-», если тройка векторов левая (рис. 14):
равно объему параллелепипеда, построенного на этих векторах, взятого со знаком «+», если тройка векторов правая, и со знаком «-», если тройка векторов левая (рис. 14):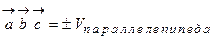 .
.
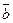
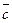
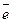
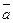
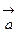 ,
, 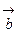 и
и  .
.
 , то
, то 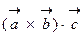



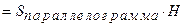
 .
. ,
, 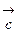 компланарны (лежат в одной плоскости или параллельных плоскостях), то их смешанное произведение равно нулю, т. е.
компланарны (лежат в одной плоскости или параллельных плоскостях), то их смешанное произведение равно нулю, т. е.  .
.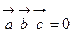 , то вектора
, то вектора 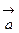 ,
,  и
и 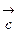 лежат в одной плоскости или параллельных плоскостях.
лежат в одной плоскости или параллельных плоскостях.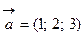 ,
,  и
и  компланарны.
компланарны.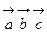
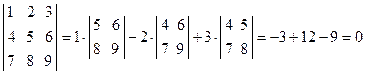 .
.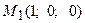 ,
,  ,
,  и
и 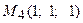 . Вычислить объем параллелепипеда.
. Вычислить объем параллелепипеда. ,
, 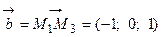 и
и 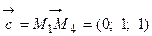 . Вычислим объем параллелепипеда
. Вычислим объем параллелепипеда



 .
. ,
, 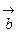 и
и 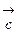 образуют правую тройку.
образуют правую тройку.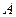 ,
, 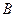 ,
, 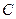 ,
,  . Варианты точек
. Варианты точек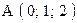

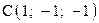
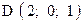
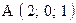

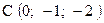

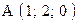
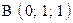
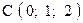
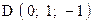

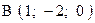

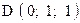
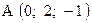
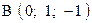
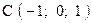
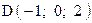
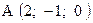
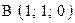
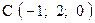

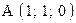
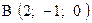
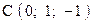

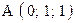
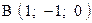
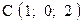
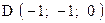
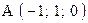

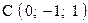
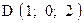
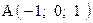
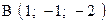
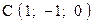
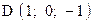




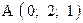
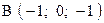
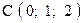
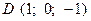
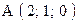
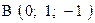
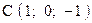
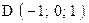
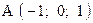
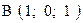
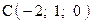
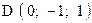
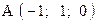
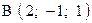

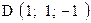
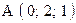
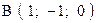
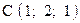
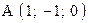



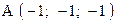
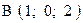

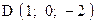
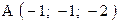




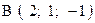
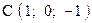
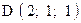
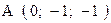

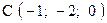
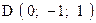
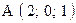

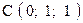
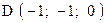



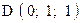
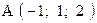
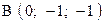
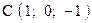

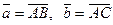 и
и  . Имеются ли среди них коллинеарные? Построить вектора
. Имеются ли среди них коллинеарные? Построить вектора 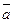 ,
, 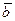 и вектора
и вектора  и
и  на плоскости
на плоскости 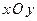 , положив аппликаторную координату вектора равной нулю. Записать разложение векторов
, положив аппликаторную координату вектора равной нулю. Записать разложение векторов 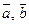 и
и 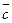 по декартовому базису
по декартовому базису 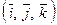 .
.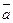 .
.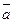 . Сравнить с ответом в предыдущем пункте. Сделать выводы.
. Сравнить с ответом в предыдущем пункте. Сделать выводы.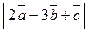 .
.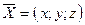 , коллинеарного вектору
, коллинеарного вектору 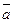 , зная, что
, зная, что 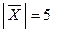 и он направлен в сторону, противоположную вектору
и он направлен в сторону, противоположную вектору 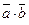 и
и 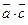 . Перпендикулярны ли вектора
. Перпендикулярны ли вектора 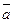 и
и  ,
,  между собой?
между собой?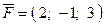 , при перемещении ее из т.
, при перемещении ее из т. 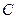 .
. треугольника
треугольника 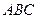 .
. и
и 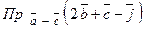 .
.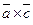 ,
, 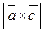 и угол
и угол 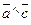 .
.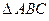 и длину его высоты, опущенной из т.
и длину его высоты, опущенной из т. 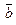 .
.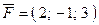 , приложенной к т.
, приложенной к т. 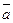 ,
, 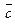 в одной плоскости? Могут ли эти вектора образовать базис пространства и почему? Если могут, то разложить по этому базису вектор
в одной плоскости? Могут ли эти вектора образовать базис пространства и почему? Если могут, то разложить по этому базису вектор 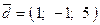 .
. и ее высоту, опущенную из т.
и ее высоту, опущенную из т. 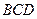 ?
?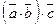 и
и 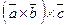 .
.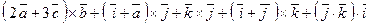 .
.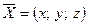 , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам 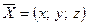 , удовлетворяющий условиям
, удовлетворяющий условиям  ,
,  ,
, 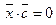 .
.


