
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричный способ решения СЛАУ.
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных Пример 2. Решить СЛАУ матричным способом Введем в рассмотрение следующие матрицы
Запишем обратную матрицу
Отсюда находим, что Метод Гаусса. Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этом разделе. Расширенная матрица для СЛАУ Примера 1 имеет вид: – умножим элементы первой строки на ментам второй строки – умножим элементы первой строки на на Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной
Вывод: Из вышеизложенного материала следует, что вне зависимости от способа решения СЛАУ всегда должен получаться один и тот же ответ. Самостоятельная работа № 1«Основы линейной алгебры» 1. Решить неравенство или уравнение. 2. Вычислить определитель четвертого порядка, преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и вычислить полученный определитель по элементам этого ряда. 3. Решить по формулам Крамера систему линейных алгебраических уравнений. 4. Решить матричным способом систему линейных алгебраических уравнений. 5. При каких значениях параметров Вариант 1 1) 3) Вариант 2 1) 3) Вариант 3 1) 3) Вариант 4 1) 3) Вариант 5 1) 3) Вариант 6 1) 3) Вариант 7 1) 3) Вариант 8 1) 3) Вариант 9 1) 3) Вариант 10 1) 3) Вариант 11 1) 3) Вариант 12 1) 3) Вариант 13 1) 3) Вариант 14 1) 3) Вариант 15 1) 3) Вариант 16 1) 3) Вариант 17 1) 3) Вариант 18 1)
3) Вариант 19 1) 3) Вариант 20 1) 3) Вариант 21 1) 3) Вариант 22 1) 3) Вариант 23 1) 3) Вариант 24 1) 3)
|
||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 86; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.2.34 (0.03 с.) |
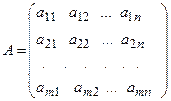 , матрицу-стол-бец неизвестных
, матрицу-стол-бец неизвестных  и матрицу-столбец свободных коэффициентов
и матрицу-столбец свободных коэффициентов  . Тогда СЛАУ можно записать в матричном виде
. Тогда СЛАУ можно записать в матричном виде 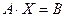 . Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу
. Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу  к матрице
к матрице 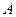 , получим
, получим 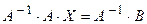 ; в силу того, что произведение
; в силу того, что произведение  и
и  , найдем
, найдем  . Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к
. Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к 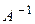 , после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.
, после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.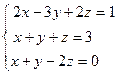 .
. ;
;  ;
; 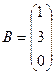 . Найдем матрицу
. Найдем матрицу 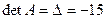 . Найдем алгебраические дополнения всех элементов
. Найдем алгебраические дополнения всех элементов 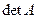 :
:

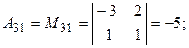
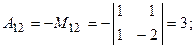
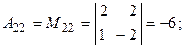
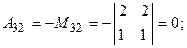
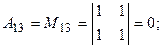
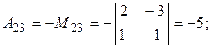
 .
. (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем найденной матрицей на матрицу-столбец свободных коэффициентов
(в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем найденной матрицей на матрицу-столбец свободных коэффициентов 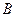 :
: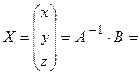
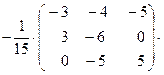
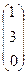
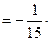

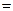
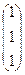 .
. . После нахождения решения СЛАУ надо сделать проверку.
. После нахождения решения СЛАУ надо сделать проверку.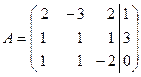 . В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы. Обменяем в расширенной матрице первую и вторую строки местами, получим
. В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы. Обменяем в расширенной матрице первую и вторую строки местами, получим 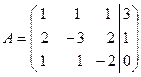 . Приведем матрицу к треугольному виду, выполнив следующие преобразования:
. Приведем матрицу к треугольному виду, выполнив следующие преобразования: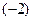 и прибавим к соответствующим эле-
и прибавим к соответствующим эле-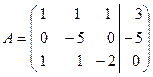 . Разделим все элементы второй строки на
. Разделим все элементы второй строки на 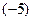 , получим
, получим 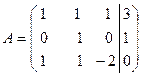 .
.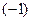 и прибавим к соответствующим элементам третьей строки
и прибавим к соответствующим элементам третьей строки 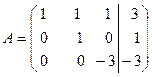 . Разделим все элементы третьей строки
. Разделим все элементы третьей строки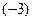 , получим
, получим 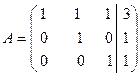 .
.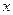 , второй – при неизвестной
, второй – при неизвестной 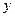 , третий – при неизвестной
, третий – при неизвестной 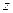 , а за вертикальной чертой находится столбец свободных коэффициентов):
, а за вертикальной чертой находится столбец свободных коэффициентов): 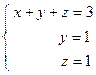 . Из первого уравнения находим, что
. Из первого уравнения находим, что 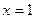 .
.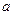 и
и 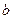 система имеет: а) единственное решение; б) не имеет решений; в) бесчисленное множество решений.
система имеет: а) единственное решение; б) не имеет решений; в) бесчисленное множество решений.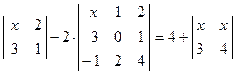 ; 2)
; 2) 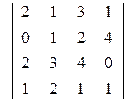 ;
; 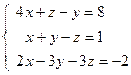 ; 4)
; 4) 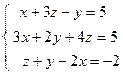 ; 5)
; 5) 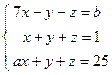 .
. 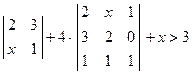 ; 2)
; 2) 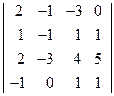 ;
; 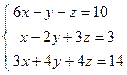 ; 4)
; 4) 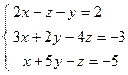 ; 5)
; 5)  .
.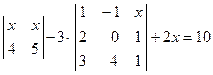 ; 2)
; 2) 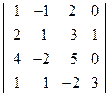 ;
;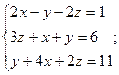 4)
4) 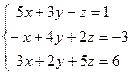 ; 5)
; 5) 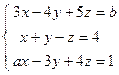 .
.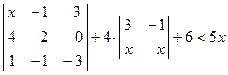 ; 2)
; 2)  ;
; 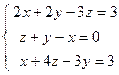 ; 4)
; 4) 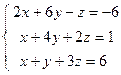 ; 5)
; 5) 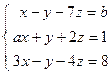 .
.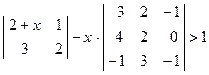 ; 2)
; 2) 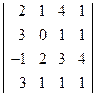 ;
;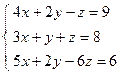 ; 4)
; 4) 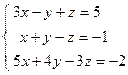 ; 5)
; 5) 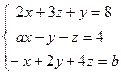 .
.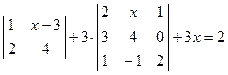 ; 2)
; 2) 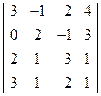 ;
; 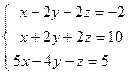 ; 4)
; 4)  ; 5)
; 5) 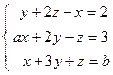 .
.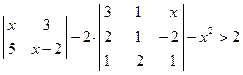 ; 2)
; 2) 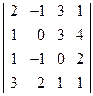 ;
; 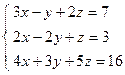 ; 4)
; 4) 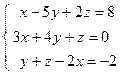 ; 5)
; 5) 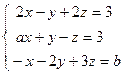 .
.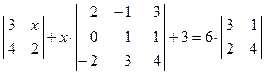 ; 2)
; 2) 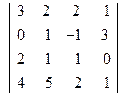 ;
; 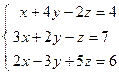 ; 4)
; 4) 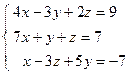 ; 5)
; 5) 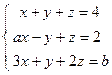 .
.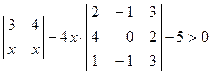 ; 2)
; 2) 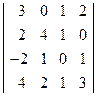 ;
;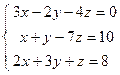 ; 4)
; 4) 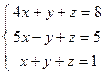 ; 5)
; 5) 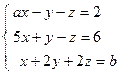 .
.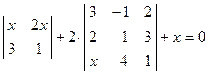 ; 2)
; 2) 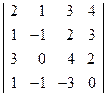 ;
; 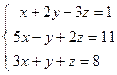 ; 4)
; 4) 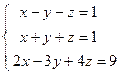 ; 5)
; 5) 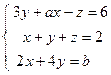 .
.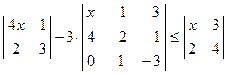 ; 2)
; 2) 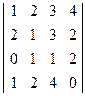 ;
; 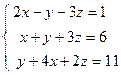 ; 4)
; 4) 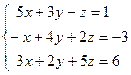 ; 5)
; 5) 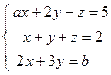 .
.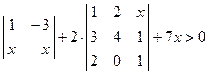 ; 2)
; 2) 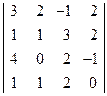 ;
;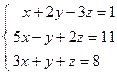 ; 4)
; 4) 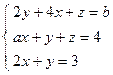 .
.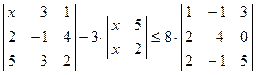 ; 2)
; 2) 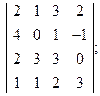
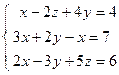 ; 4)
; 4)  ; 5)
; 5) 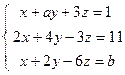 .
.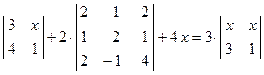 ; 2)
; 2) 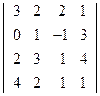 ;
; 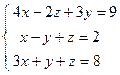 ; 4)
; 4) 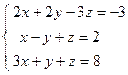 ; 5)
; 5) 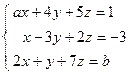 .
.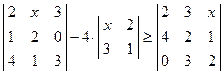 ; 2)
; 2) 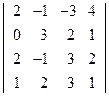 ;
; 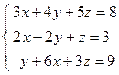 ; 4)
; 4) 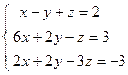 ; 5)
; 5) 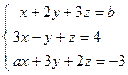 .
.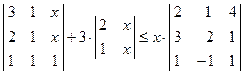 ; 2)
; 2) 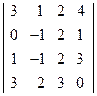 ;
; 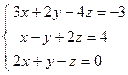 ; 4)
; 4) 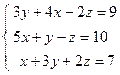 ; 5)
; 5) 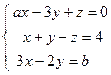 .
.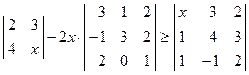 ; 2)
; 2) 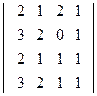 ;
; 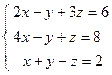 ; 4)
; 4) 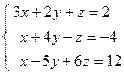 ; 5)
; 5) 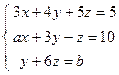 .
.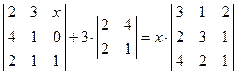 ; 2)
; 2) 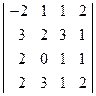 ;
; 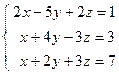 ; 4)
; 4) 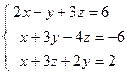 ; 5)
; 5) 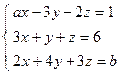 .
.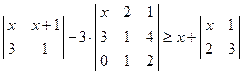 ; 2)
; 2) 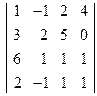 ;
; 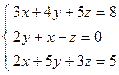 ; 4)
; 4) 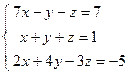 ; 5)
; 5) 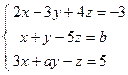 .
.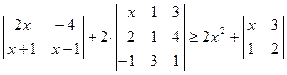 ; 2)
; 2) 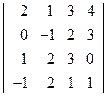 ;
; 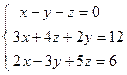 ; 4)
; 4) 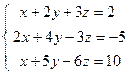 ; 5)
; 5) 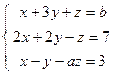 .
.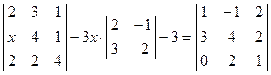 ; 2)
; 2) 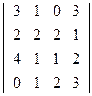 ;
; 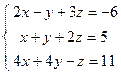 ; 4)
; 4) 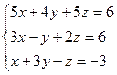 ; 5)
; 5) 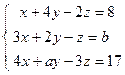 .
.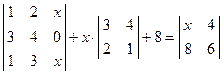 ; 2)
; 2) 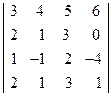 ;
; 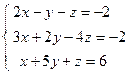 ; 4)
; 4) 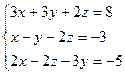 ; 5)
; 5) 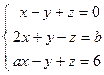 .
.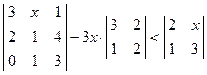 ; 2)
; 2) 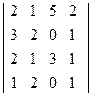 ;
; 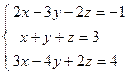 ; 4)
; 4) 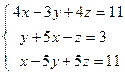 ; 5)
; 5) 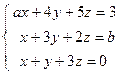 .
.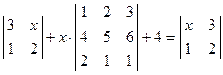 ; 2)
; 2) 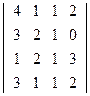 ;
; 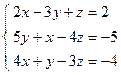 ; 4)
; 4) 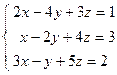 ; 5)
; 5) 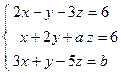 .
.


