
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторов.
О3. Скалярным произведением двух векторов Пример 1. Вычислить скалярное векторов Используя определение скалярного произведения, находим З2. Используя определения проекции и скалярного произведения двух векторов, можно записать, что Рассмотрим свойства скалярного произведения: 1. 4. Формула для скалярного произведения векторов Через проекции перемножаемых векторов.
Пусть даны вектора
Используя эту таблицу, вычислим скалярное произведение векторов
Сл1. Если вектор Сл2. Если
Сл3. Проекция вектора Пример 2. Найти, при каком значении Условием перпендикулярности векторов является обращение в нуль их скалярного произведения, поэтому воспользуемся следствием 1 из теоремы 2:
“Векторное и смешанное произведения векторов” Векторное произведение. О2. Тройка векторов Пример 1.
Рис. 9. Правая (а) и левая (б) тройки векторов. О3. Векторным произведением – по модулю численно равен площади параллелограмма, построенного на векторах – перпендикулярен плоскости, в которой лежат вектора – тройка векторов Из определения векторного произведения следует, что направление вектора
Рис. 10. Площадь параллелограмма, определяющего длину вектора Из треугольника Векторное произведение векторов обладает следующими свойствами: 1. 4. Если вектор
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.190.58 (0.015 с.) |
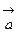 и
и 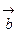 называется число (скаляр) равное произведению модулей этих векторов на косинус угла между этими векторами:
называется число (скаляр) равное произведению модулей этих векторов на косинус угла между этими векторами: 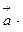
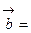
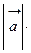
 , где
, где 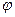 – угол между векторами
– угол между векторами 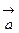 и
и 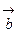 , если их длины равны 2 и 5, соответственно, а угол между векторами равен
, если их длины равны 2 и 5, соответственно, а угол между векторами равен 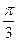 .
.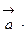
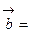

 .
.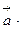
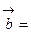
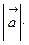
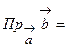
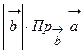 . Откуда можно найти проекцию одного вектора на другой, например,
. Откуда можно найти проекцию одного вектора на другой, например,  .
.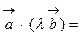
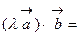
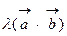 ; 2.
; 2. 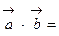
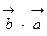 ; 3.
; 3. 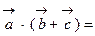

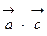 ;
; 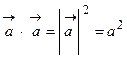 ; 5. Если вектор
; 5. Если вектор 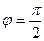 ), то их скалярное произведение равно нулю:
), то их скалярное произведение равно нулю: 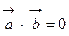 . Свойство 5 определяет условие перпендикулярности векторов.
. Свойство 5 определяет условие перпендикулярности векторов.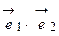
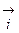
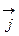
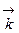
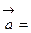

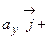
 и
и 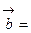
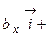
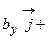
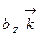 . Составим таблицу скалярных произведений ортов осей
. Составим таблицу скалярных произведений ортов осей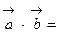
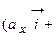
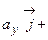
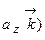


 =
= 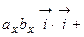
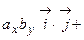
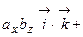
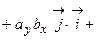
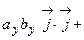
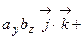
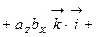
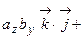

 .
.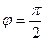 ), то их скалярное произведение равно нулю, то есть
), то их скалярное произведение равно нулю, то есть 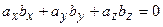 .
.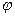 - угол между векторами
- угол между векторами 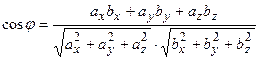 .
.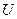 ) равна скалярному произ-ведению вектора
) равна скалярному произ-ведению вектора 
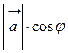 .
.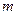 вектора
вектора 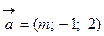 и
и  перпендикулярны.
перпендикулярны.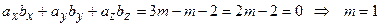 .
.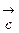 называется правой (левой), если обход векторов
называется правой (левой), если обход векторов 
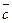 а)
а) 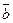
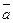
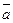
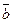
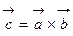 , который
, который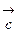 определяется по правилу правого винта: при вращении вектора
определяется по правилу правого винта: при вращении вектора 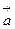 и
и 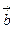 (рис. 10):
(рис. 10):
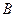
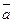
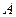

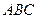 высота
высота 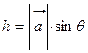 , тогда
, тогда 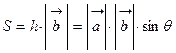 , следовательно, длина вектора
, следовательно, длина вектора 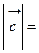
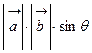 , где
, где 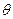 - угол между векторами
- угол между векторами 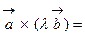
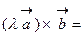
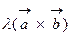 ; 2.
; 2. 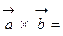
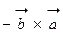 ; 3.
; 3. 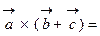
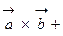
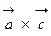 ;
; 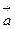 коллинеарен вектору
коллинеарен вектору 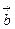 (
(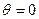 или
или  ), то их векторное произведение равно нулю:
), то их векторное произведение равно нулю: 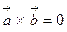 . Свойство 4 определяет второе условие коллинеарности векторов.
. Свойство 4 определяет второе условие коллинеарности векторов. 


