
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула для векторного произведения векторов
Через проекции перемножаемых векторов. Запишем вектора
Для доказательства формулы теоремы составим таблицу векторных произведений ортов осей
Используя эту таблицу, вычислим векторное произведение векторов
Отсюда следует, что
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, т. е. Пример 1. Найти, при каком значении параметра Согласно свойству 4 для векторного произведения найдем векторное произведение заданных векторов
Так как вектор Пример 2. Найти векторное произведение векторов
Приложения векторного произведения. 1. Физика. Пусть точка начала вектора
Рис. 11. Момент силы 2. Геометрия. Даны три точки
Рис. 12. Площадь треугольника Проекции векторов равны Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов
Пример 3. Даны три точки
Введем в рассмотрение вектора Следовательно, площадь треугольника равна 3. Тригонометрия. Выведем формулу для Пусть в плоской декартовой системе координат даны вектора
Рис. 13. Синус суммы двух углов. Проекции векторов равны
Используя формулу для векторного произведения векторов и свойство 4 для определителей, получим
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.20.57 (0.017 с.) |
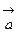 и
и 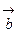 в декартовом базисе:
в декартовом базисе: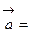
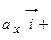
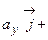
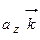 и
и 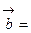
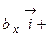
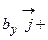
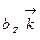 .
.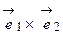
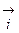
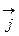
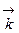
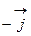
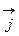
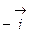
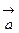 и
и 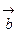 :
: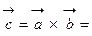
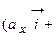
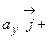
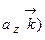
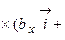
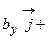
 =
= 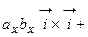
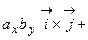
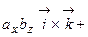
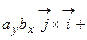
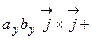
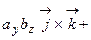
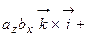
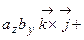
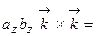
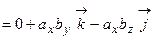
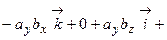
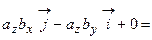
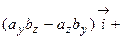
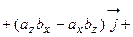
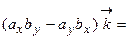
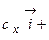
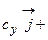
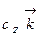 .
.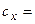
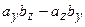 ;
; 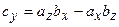 ;
; 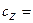
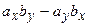 . Для запоминания этих формул существует мнемоническое правило: надо запомнить переход проекций от одной к другой
. Для запоминания этих формул существует мнемоническое правило: надо запомнить переход проекций от одной к другой 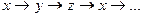 ; для нахождения, например проекции
; для нахождения, например проекции 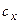 , надо взять компоненту
, надо взять компоненту 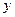 первого вектора и умножить на компоненту
первого вектора и умножить на компоненту  второго вектора, а затем вычесть их произведение, обменяв местами обозначение компонент. С другой стороны, полученную формулу можно записать в виде
второго вектора, а затем вычесть их произведение, обменяв местами обозначение компонент. С другой стороны, полученную формулу можно записать в виде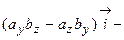
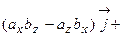
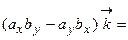
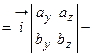
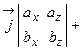
 .
.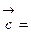
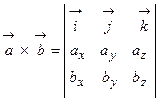 .
.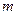 вектор
вектор 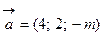 колли-неарен вектору
колли-неарен вектору 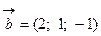 .
.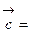
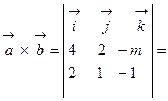
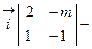
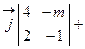
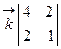 =
= 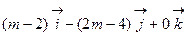 .
. должен быть нулевым, то все его проекции должны быть рав-ными нулю, следовательно,
должен быть нулевым, то все его проекции должны быть рав-ными нулю, следовательно, 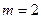 .
. и
и 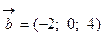 .
.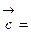
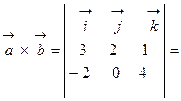
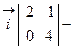
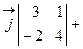
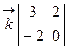 =
= 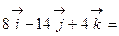
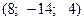 .
. закреплена, а к его концу приложена сила
закреплена, а к его концу приложена сила 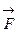 , тогда момент этой силы будет равен
, тогда момент этой силы будет равен 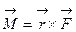 (рис. 11).
(рис. 11).
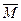
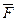
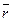
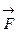 .
.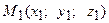 ,
, 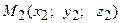 и
и 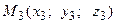 . Требуется вычислить площадь треугольника
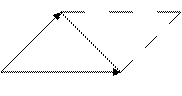
. Требуется вычислить площадь треугольника 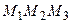 (рис. 14). Введем в рассмотрение вектора
(рис. 14). Введем в рассмотрение вектора 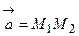 и
и 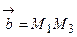 .
.
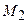
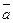
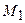
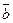
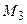
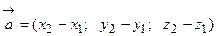 и
и 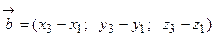 .
.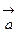 и
и 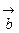 , то
, то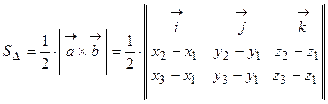 .
.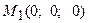 ,
, 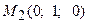 и
и 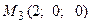 . Вычислить площадь треугольника
. Вычислить площадь треугольника 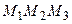 .
.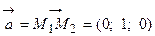 и
и 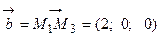 , вычислим их векторное произведение
, вычислим их векторное произведение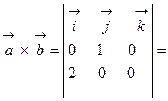
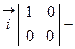
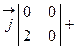
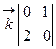 =
= 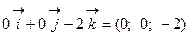 .
.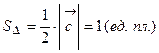 .
.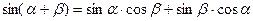 .
.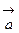 и
и 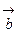 , которые образуют с положительным направлением оси
, которые образуют с положительным направлением оси 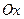 углы
углы 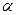 и
и 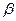 , соответственно (рис. 13).
, соответственно (рис. 13).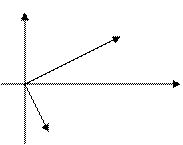
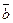
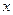
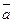
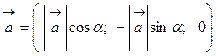 и
и 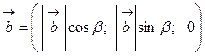 .
. . Раскрыв этот определитель по элементам третьего столбца, получим
. Раскрыв этот определитель по элементам третьего столбца, получим 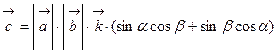 . Длина этого вектора равна
. Длина этого вектора равна 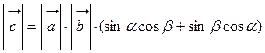 . С другой стороны, по определению векторного произведения его длина равна
. С другой стороны, по определению векторного произведения его длина равна 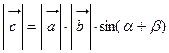 . Сравнивая две полученные формулы, получаем формулу для синуса суммы двух углов. В частности, при
. Сравнивая две полученные формулы, получаем формулу для синуса суммы двух углов. В частности, при 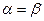 получаем, что
получаем, что 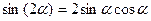 .
.


