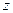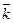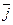Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
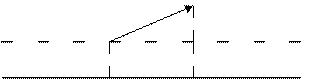
Проекция вектора на произвольную ось.
Пусть дана ось
Рис. 5. Проекция вектора на заданную ось. Из начала и конца вектора О9. Проекцией вектора Из рисунка видно, что отрезок личина Декартова система координат и вектора. О10. Направленная прямая с выбранным началом отсчета и масштабом из-мерения называется числовой осью. О11. Две (три) взаимно перпендикулярные числовые оси называются декартовой системой координат на плоскости (в пространстве). Рассмотрим декартову систему координат на плоскости и спроектируем вектор
Рис. 6. Проекции вектора на оси декартовой системы координат. Из рисунка видно, что проекции вектора О12. Проекции Используя теорему Пифагора, найдем длину вектора
4. Направляющие косинусы вектора Обозначим углы, которые образует вектор Тогда О13. Величины Вычислив квадрат модуля вектора
5. Способы задания вектора. 1. Задаются координаты начальной и конечной точек вектора 2. Задаются координаты вектора 3. Задаются длина вектора и два любых угла, которые образует вектор
но так как по условию Деление отрезка в заданном отношении. Пусть в пространственной декартовой системе отсчета даны две точки
Рис. 7. Деление отрезка в заданном отношении. Из рис. 7 видно, что В силу того, что “Скалярное произведение векторов и его свойства” Понятие базиса. О1. Любые два (три) неколлинеарных (некомпланарных) вектора образуют базис. В трехмерном пространстве произвольный вектор О2. Ортом направления оси ( Рассмотрим пространственную декартову систему координат, по всем осям (абсцисс –
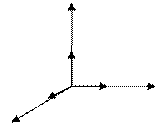
Рис. 8. Орты (единичные вектора) декартовой системы координат.
|
||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.228.95 (0.014 с.) |
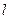 и вектор
и вектор 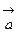 (рис. 5). Проведем через начало вектора
(рис. 5). Проведем через начало вектора 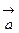 прямую, которая параллельна оси
прямую, которая параллельна оси 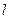 , угол между прямой и вектором
, угол между прямой и вектором 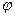 .
.
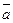
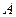
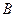
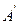
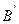
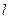
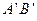 .
.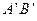 , взятая со знаком «+», если угол
, взятая со знаком «+», если угол 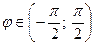 , и со знаком «-», если
, и со знаком «-», если 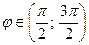 .
.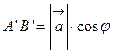 , следовательно,
, следовательно, 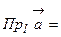
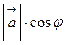 . Из этой формулы видно, что при
. Из этой формулы видно, что при  , а при
, а при 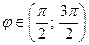 ве-
ве-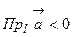 . При
. При 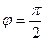 (или
(или 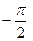 ) проекция равна нулю, т. е.
) проекция равна нулю, т. е. 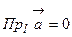 .
.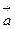 на координатные оси (рис. 6):
на координатные оси (рис. 6):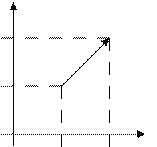
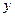
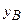
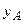
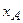
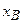
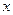
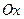 ) равна
) равна 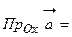
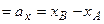 , проекция на ось ординат (
, проекция на ось ординат ( )
) 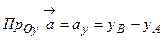 (в пространстве проекция на ось аппликат (
(в пространстве проекция на ось аппликат ( ) –
) – 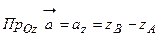 ).
).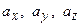 называются координатами вектора
называются координатами вектора 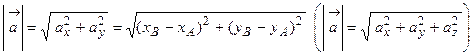 .
.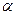 ,
, 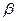 ,
, 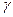 .
.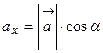 ;
; 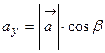 ;
; 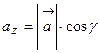 .
.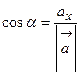 ,
, 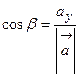 ,
, 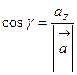 называются направляющими косинусами вектора
называются направляющими косинусами вектора 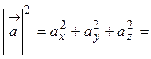
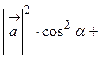
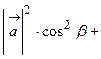
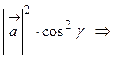
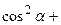
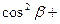
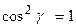 .
.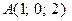 и
и 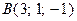 . Тогда
. Тогда 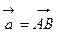 :
: 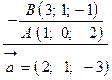 .
.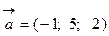 .
.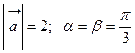 ,
, 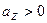 . Тогда
. Тогда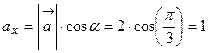 ,
, 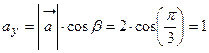 ,
, 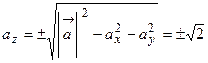 ,
,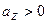 , то
, то 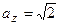 . Следовательно,
. Следовательно, 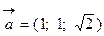 .
.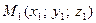 и
и 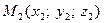 . Требуется найти на отрезке
. Требуется найти на отрезке 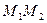 такую точку
такую точку 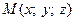 , чтобы
, чтобы 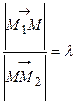 , где
, где 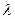 – заданное число.
– заданное число.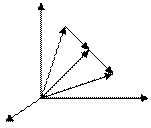
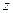
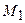
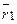
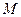
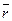
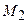
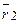
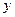
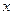
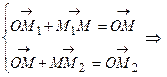
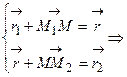
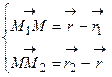 .
.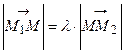 и
и 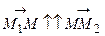 , то
, то 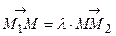 . Подставляя это равенство в систему и исключая вектор
. Подставляя это равенство в систему и исключая вектор  , найдем, что
, найдем, что 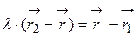 . Отсюда найдем вектор
. Отсюда найдем вектор 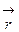 :
: 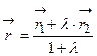 . В проекциях на координатные оси это равенство равносильно системе равенств
. В проекциях на координатные оси это равенство равносильно системе равенств 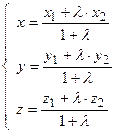 , которая определяет деление отрезка в заданном отношении. Если точка
, которая определяет деление отрезка в заданном отношении. Если точка 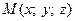 делит отрезок
делит отрезок 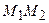 пополам (
пополам (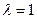 ), то система полученных равенств принимает вид известный из курса математики средней школы
), то система полученных равенств принимает вид известный из курса математики средней школы 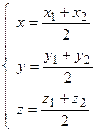 .
.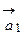 ,
, 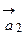 и
и 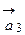 так:
так: 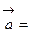
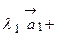
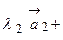
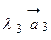 , причем единственным образом;
, причем единственным образом; 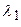 ,
, 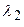 ,
, 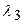 – вещественные числа.
– вещественные числа.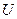 ) называется вектор единичной длины в выбранном масштабе измерения, сонаправленный с этой осью (
) называется вектор единичной длины в выбранном масштабе измерения, сонаправленный с этой осью (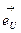 ).
).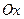 , ординат –
, ординат – 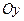 и аппликат –
и аппликат – 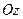 ) выберем одинаковый масштаб измерения. Вдоль положительного направления каждой оси отложим отрезки единичной длины. Обозначим орты осей:
) выберем одинаковый масштаб измерения. Вдоль положительного направления каждой оси отложим отрезки единичной длины. Обозначим орты осей: 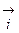 ,
, 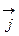 ,
, 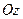 – через
– через 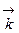 (рис. 8). Так как вектора
(рис. 8). Так как вектора 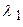 ,
, 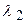 и
и 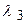 выступают проекции вектора на соответствующие оси:
выступают проекции вектора на соответствующие оси: 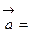
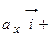
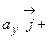
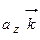 .
.