
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Основы линейной алгебрыСтр 1 из 8Следующая ⇒
Специальностей ОМД и ТО физико-металлургического факультета Донецк
УДК 51
На протяжении многих лет ведущие преподаватели кафедр «Высшая математика» и «Математическая физика» разрабатывали методические указания и индивидуализированные задания для самостоятельной работы студентов всех специи-альностей, обучение по которым проводится в Донецком национальном техническом университете. Основными работами преподавателей кафедр «Высшая математика» и «Математическая физика» являются: 1. Методические указания к организации самостоятельной работы при изучении линейной алгебры и аналитической геометрии. – Н.Г. Плаксина, С.Н. Мартынова. – Донецк: ДПИ, 1988. – 44с. 2. Методические указания к выполнению лабораторных работ по курсу „Высшая математика” – Н.С. Ищенко, Н.Г. Плаксина, В.Я. Шварц. – Донецк: ДПИ, 1983. – 28с. 3. Методические указания к выполнению типовых расчетов по курсу „Высшая математика”(I семестр). – Н.С. Ищенко, О.П. Кирсанова, Л.М. Шевченко. – Донецк: ДПИ, 1984. – 68с. 4. Задания к индивидуальным практическим занятиям по разделу курса высшей математики „Дифференциальное исчисление”. – Ю.Л. Носенко, Л.М. Шевченко. – До-нецк: ДПИ, 1987. – 36с. 5. Задания к индивидуальным практическим занятиям по разделу курса высшей математики „Интегральное исчисление”. – Ю.Л. Носенко, Н.П. Носенко. – Донецк: ДПИ, 1986. – 56с. 6. Методические указания по курсу „Высшая математика” (Раздел „Функции нескольких переменных”). – Н.Г. Плаксина, С.Н. Мартынова. – Донецк: ДПИ, 1992. – 44с. 7. Методические указания к типовым расчетам по разделу курса высшей мате-матики „Обыкновенные дифференциальные уравнения”. – Н.Г. Плаксина – Донецк: ДПИ, 1987. – 44с. 8. Методические указания по организации самостоятельной работы студентов при изучении курса высшей математики. Раздел „Ряды”. – Н.П. Носенко, Ю.Л. Носенко. – Донецк: ДПИ, 1988.- 40с. 9. Методические указания к выполнению типового расчета по курсу теории вероятностей, ч.1(2). – А.К. Зубченко. – Донецк: ДПИ, 1983(84). – 42с.(48с.) 10. Методические указания к выполнению семестрового индивидуального задания по математической статистике. – Ю.Ф. Косолапов, Н.Г. Плаксина. – Донецк: ДПИ, 1989. – 48с. В связи с тем, что при выдаче индивидуализированных заданий на семестр позволяет студентам спланировать время на их выполнение, возникла необходимость в дополнение к изданным методическим указаниям собрать задания для самостоятельной работы в едином сборнике. Кроме того, в связи с уменьшением времени, отводимого на изучение курса высшей математики в техническом университете, ряд заданий был исключен, преобразован, заменен другими примерами. На выполнение каждой самостоятельной работы отводится определенное количество времени согласно учебному плану для данной специальности.
1 курс1 семестр Тема: Основы линейной алгебры “Определители и их свойства” “Матрицы и действия с ними” “Методы решения систем линейных алгебраических уравнений” Тема: Элементы векторной алгебры “Векторы. Проекции” “Скалярное произведение векторов и его свойства” “Векторное и смешанное произведения векторов” Тема: Аналитическая геометрия на плоскости и в пространстве “Прямая на плоскости. Основные задачи” “Кривые второго порядка” “Преобразования декартовой системы координат. Полярная система координат” “Плоскость в пространстве” “Прямая в пространстве” Метод Крамера. О1. Системой линейных алгебраических уравнений (СЛАУ) называется выражение О2. Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы Крамер предложил следующий метод решения СЛАУ: умножим главный опре-делитель на Второй столбец умножим на
Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, то есть О3. Определитель Поступая аналогично найдем все вспомогательные определители СЛАУ:
Для того чтобы найти вспомогательный определитель
О4. Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы: – если главный определитель системы отличен от нуля ( – если главный определитель системы равен нулю ( – если все определители системы равны нулю ( Пример 1. Решить СЛАУ методом Крамера Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Воспользуемся формулами Крамера
После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляются в нормализованную си-стему линейных алгебраических уравнений. Выполним проверку
Метод Гаусса. Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этом разделе. Расширенная матрица для СЛАУ Примера 1 имеет вид: – умножим элементы первой строки на ментам второй строки – умножим элементы первой строки на на Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной Вывод: Из вышеизложенного материала следует, что вне зависимости от способа решения СЛАУ всегда должен получаться один и тот же ответ. Самостоятельная работа № 1«Основы линейной алгебры» 1. Решить неравенство или уравнение. 2. Вычислить определитель четвертого порядка, преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и вычислить полученный определитель по элементам этого ряда. 3. Решить по формулам Крамера систему линейных алгебраических уравнений.
4. Решить матричным способом систему линейных алгебраических уравнений. 5. При каких значениях параметров Вариант 1 1) 3) Вариант 2 1) 3) Вариант 3 1) 3) Вариант 4 1) 3) Вариант 5 1) 3) Вариант 6 1) 3) Вариант 7 1) 3) Вариант 8 1) 3) Вариант 9 1) 3) Вариант 10 1) 3) Вариант 11 1) 3) Вариант 12 1) 3) Вариант 13 1) 3) Вариант 14 1) 3) Вариант 15 1) 3) Вариант 16 1) 3) Вариант 17 1) 3) Вариант 18 1) 3) Вариант 19 1) 3) Вариант 20 1) 3) Вариант 21 1) 3) Вариант 22 1) 3) Вариант 23 1) 3) Вариант 24 1) 3) Понятие базиса. О1. Любые два (три) неколлинеарных (некомпланарных) вектора образуют базис. В трехмерном пространстве произвольный вектор О2. Ортом направления оси ( Рассмотрим пространственную декартову систему координат, по всем осям (абсцисс –
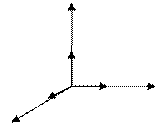
Рис. 8. Орты (единичные вектора) декартовой системы координат. Векторное произведение. О2. Тройка векторов Пример 1.
Рис. 9. Правая (а) и левая (б) тройки векторов. О3. Векторным произведением – по модулю численно равен площади параллелограмма, построенного на векторах – перпендикулярен плоскости, в которой лежат вектора – тройка векторов Из определения векторного произведения следует, что направление вектора
Рис. 10. Площадь параллелограмма, определяющего длину вектора Из треугольника Векторное произведение векторов обладает следующими свойствами: 1. 4. Если вектор Специальностей ОМД и ТО физико-металлургического факультета Донецк
УДК 51
На протяжении многих лет ведущие преподаватели кафедр «Высшая математика» и «Математическая физика» разрабатывали методические указания и индивидуализированные задания для самостоятельной работы студентов всех специи-альностей, обучение по которым проводится в Донецком национальном техническом университете. Основными работами преподавателей кафедр «Высшая математика» и «Математическая физика» являются:
1. Методические указания к организации самостоятельной работы при изучении линейной алгебры и аналитической геометрии. – Н.Г. Плаксина, С.Н. Мартынова. – Донецк: ДПИ, 1988. – 44с. 2. Методические указания к выполнению лабораторных работ по курсу „Высшая математика” – Н.С. Ищенко, Н.Г. Плаксина, В.Я. Шварц. – Донецк: ДПИ, 1983. – 28с. 3. Методические указания к выполнению типовых расчетов по курсу „Высшая математика”(I семестр). – Н.С. Ищенко, О.П. Кирсанова, Л.М. Шевченко. – Донецк: ДПИ, 1984. – 68с. 4. Задания к индивидуальным практическим занятиям по разделу курса высшей математики „Дифференциальное исчисление”. – Ю.Л. Носенко, Л.М. Шевченко. – До-нецк: ДПИ, 1987. – 36с. 5. Задания к индивидуальным практическим занятиям по разделу курса высшей математики „Интегральное исчисление”. – Ю.Л. Носенко, Н.П. Носенко. – Донецк: ДПИ, 1986. – 56с. 6. Методические указания по курсу „Высшая математика” (Раздел „Функции нескольких переменных”). – Н.Г. Плаксина, С.Н. Мартынова. – Донецк: ДПИ, 1992. – 44с. 7. Методические указания к типовым расчетам по разделу курса высшей мате-матики „Обыкновенные дифференциальные уравнения”. – Н.Г. Плаксина – Донецк: ДПИ, 1987. – 44с. 8. Методические указания по организации самостоятельной работы студентов при изучении курса высшей математики. Раздел „Ряды”. – Н.П. Носенко, Ю.Л. Носенко. – Донецк: ДПИ, 1988.- 40с. 9. Методические указания к выполнению типового расчета по курсу теории вероятностей, ч.1(2). – А.К. Зубченко. – Донецк: ДПИ, 1983(84). – 42с.(48с.) 10. Методические указания к выполнению семестрового индивидуального задания по математической статистике. – Ю.Ф. Косолапов, Н.Г. Плаксина. – Донецк: ДПИ, 1989. – 48с. В связи с тем, что при выдаче индивидуализированных заданий на семестр позволяет студентам спланировать время на их выполнение, возникла необходимость в дополнение к изданным методическим указаниям собрать задания для самостоятельной работы в едином сборнике. Кроме того, в связи с уменьшением времени, отводимого на изучение курса высшей математики в техническом университете, ряд заданий был исключен, преобразован, заменен другими примерами. На выполнение каждой самостоятельной работы отводится определенное количество времени согласно учебному плану для данной специальности.
1 курс1 семестр Тема: Основы линейной алгебры “Определители и их свойства” “Матрицы и действия с ними” “Методы решения систем линейных алгебраических уравнений”
|
|||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.33.41 (0.141 с.) |
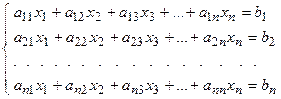 , где числа
, где числа 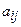 называются коэффициентами при неизвестных
называются коэффициентами при неизвестных 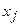 , а числа
, а числа 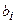 называются свободными коэффициентами.
называются свободными коэффициентами.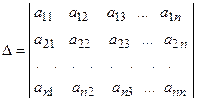 .
.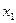 , для этого умножим все элементы первого столбца на эту неиз-вестную:
, для этого умножим все элементы первого столбца на эту неиз-вестную: 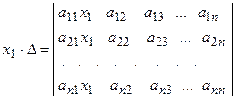 .
.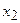 , третий столбец – на
, третий столбец – на 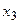 , …,
, …, 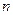 -ый столбец – на
-ый столбец – на 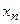 и все эти произведения прибавим к первому столбцу, при этом произведение
и все эти произведения прибавим к первому столбцу, при этом произведение 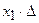 не изменится:
не изменится: 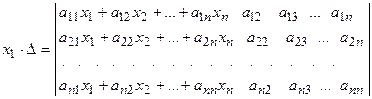 .
.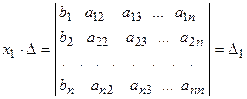 .
.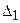 называется первым вспомогательным определителем СЛАУ.
называется первым вспомогательным определителем СЛАУ.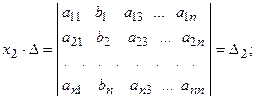
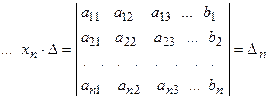 .
.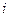 , надо в главном определителе СЛАУ заменить столбец
, надо в главном определителе СЛАУ заменить столбец 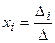 .
.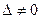 ), то система имеет единственное решение;
), то система имеет единственное решение;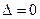 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля (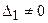 или
или 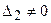 , или …, или
, или …, или 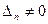 ), то система не имеет решений (деление на нуль запрещено(!!!));
), то система не имеет решений (деление на нуль запрещено(!!!));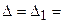
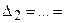
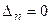 ), то система уравнений имеет бесчисленное множество решений.
), то система уравнений имеет бесчисленное множество решений.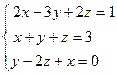 .
.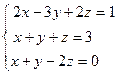 . Найдем главный определитель СЛАУ
. Найдем главный определитель СЛАУ 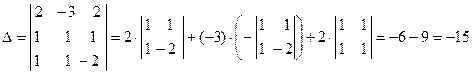 . Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
. Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя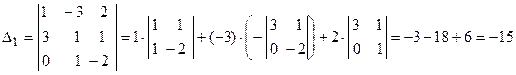 ;
;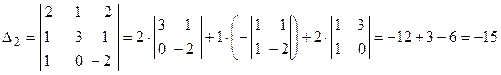 ;
; .
.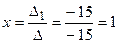 ;
; 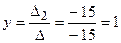 ;
; 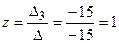 .
.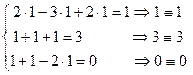 . Отсюда видно, что СЛАУ решена верно.
. Отсюда видно, что СЛАУ решена верно.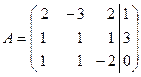 . В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы. Обменяем в расширенной матрице первую и вторую строки местами, получим
. В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы. Обменяем в расширенной матрице первую и вторую строки местами, получим 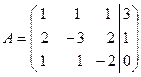 . Приведем матрицу к треугольному виду, выполнив следующие преобразования:
. Приведем матрицу к треугольному виду, выполнив следующие преобразования: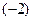 и прибавим к соответствующим эле-
и прибавим к соответствующим эле-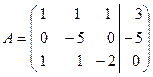 . Разделим все элементы второй строки на
. Разделим все элементы второй строки на 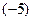 , получим
, получим 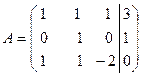 .
.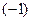 и прибавим к соответствующим элементам третьей строки
и прибавим к соответствующим элементам третьей строки 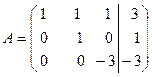 . Разделим все элементы третьей строки
. Разделим все элементы третьей строки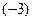 , получим
, получим 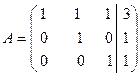 .
.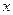 , второй – при неизвестной
, второй – при неизвестной 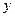 , третий – при неизвестной
, третий – при неизвестной 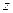 , а за вертикальной чертой находится столбец свободных коэффициентов):
, а за вертикальной чертой находится столбец свободных коэффициентов): 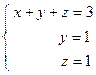 . Из первого уравнения находим, что
. Из первого уравнения находим, что 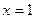 .
.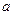 и
и 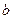 система имеет: а) единственное решение; б) не имеет решений; в) бесчисленное множество решений.
система имеет: а) единственное решение; б) не имеет решений; в) бесчисленное множество решений.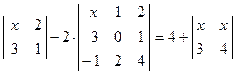 ; 2)
; 2) 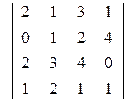 ;
; 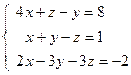 ; 4)
; 4) 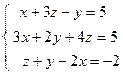 ; 5)
; 5) 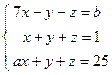 .
. 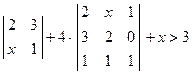 ; 2)
; 2) 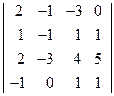 ;
; 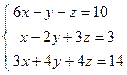 ; 4)
; 4) 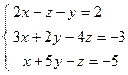 ; 5)
; 5)  .
.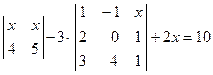 ; 2)
; 2) 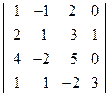 ;
;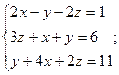 4)
4) 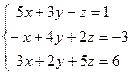 ; 5)
; 5) 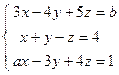 .
.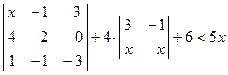 ; 2)
; 2)  ;
; 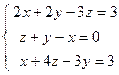 ; 4)
; 4) 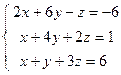 ; 5)
; 5) 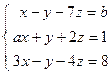 .
.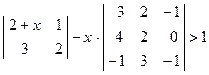 ; 2)
; 2) 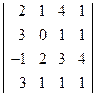 ;
;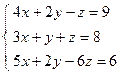 ; 4)
; 4) 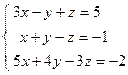 ; 5)
; 5) 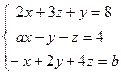 .
.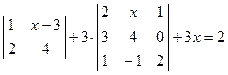 ; 2)
; 2) 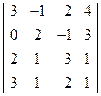 ;
; 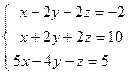 ; 4)
; 4)  ; 5)
; 5) 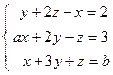 .
.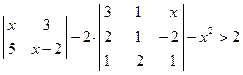 ; 2)
; 2) 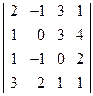 ;
; 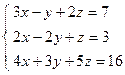 ; 4)
; 4) 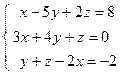 ; 5)
; 5) 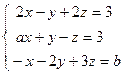 .
.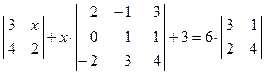 ; 2)
; 2) 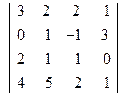 ;
; 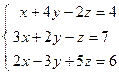 ; 4)
; 4) 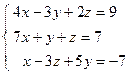 ; 5)
; 5) 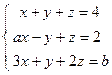 .
.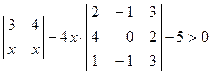 ; 2)
; 2) 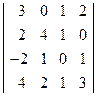 ;
;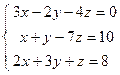 ; 4)
; 4) 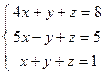 ; 5)
; 5) 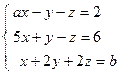 .
.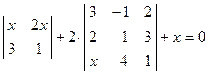 ; 2)
; 2) 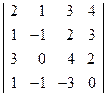 ;
; 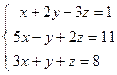 ; 4)
; 4) 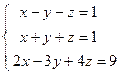 ; 5)
; 5) 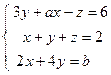 .
.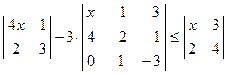 ; 2)
; 2) 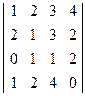 ;
; 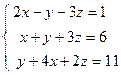 ; 4)
; 4) 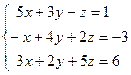 ; 5)
; 5) 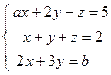 .
.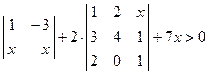 ; 2)
; 2) 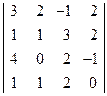 ;
;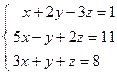 ; 4)
; 4) 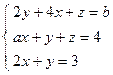 .
.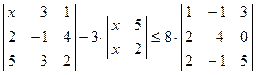 ; 2)
; 2) 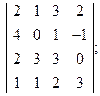
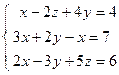 ; 4)
; 4)  ; 5)
; 5) 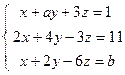 .
.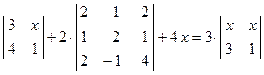 ; 2)
; 2) 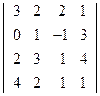 ;
; 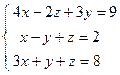 ; 4)
; 4) 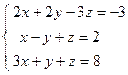 ; 5)
; 5) 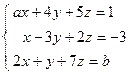 .
.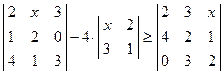 ; 2)
; 2) 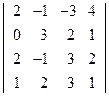 ;
; 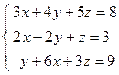 ; 4)
; 4) 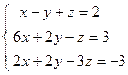 ; 5)
; 5) 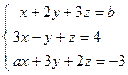 .
.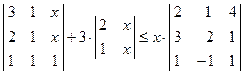 ; 2)
; 2) 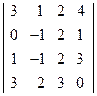 ;
; 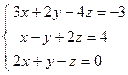 ; 4)
; 4) 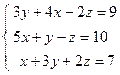 ; 5)
; 5) 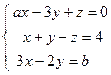 .
.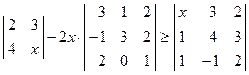 ; 2)
; 2) 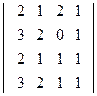 ;
; 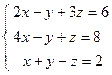 ; 4)
; 4) 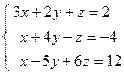 ; 5)
; 5) 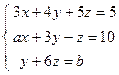 .
.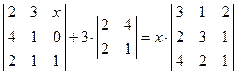 ; 2)
; 2) 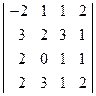 ;
; 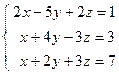 ; 4)
; 4) 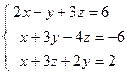 ; 5)
; 5) 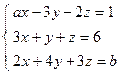 .
.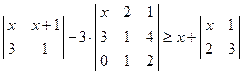 ; 2)
; 2) 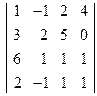 ;
; 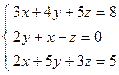 ; 4)
; 4) 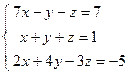 ; 5)
; 5) 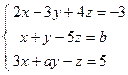 .
.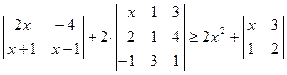 ; 2)
; 2) 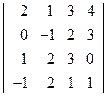 ;
; 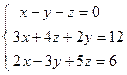 ; 4)
; 4) 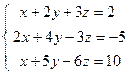 ; 5)
; 5) 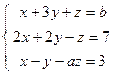 .
.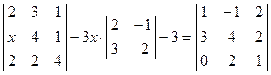 ; 2)
; 2) 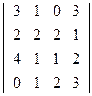 ;
; 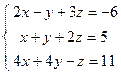 ; 4)
; 4) 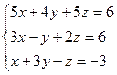 ; 5)
; 5) 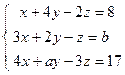 .
.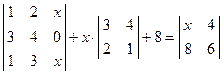 ; 2)
; 2) 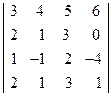 ;
; 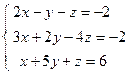 ; 4)
; 4) 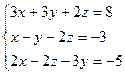 ; 5)
; 5) 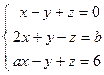 .
.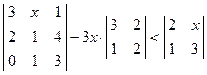 ; 2)
; 2) 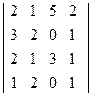 ;
; 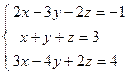 ; 4)
; 4) 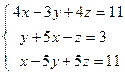 ; 5)
; 5) 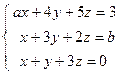 .
.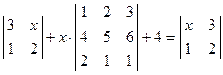 ; 2)
; 2) 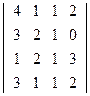 ;
; 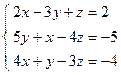 ; 4)
; 4) 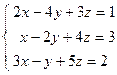 ; 5)
; 5) 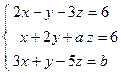 .
.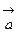 разлагается по базису векторов
разлагается по базису векторов 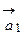 ,
, 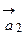 и
и 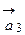 так:
так: 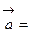
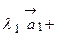
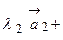
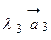 , причем единственным образом;
, причем единственным образом; 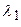 ,
, 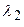 ,
, 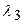 – вещественные числа.
– вещественные числа.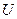 ) называется вектор единичной длины в выбранном масштабе измерения, сонаправленный с этой осью (
) называется вектор единичной длины в выбранном масштабе измерения, сонаправленный с этой осью (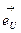 ).
).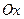 , ординат –
, ординат – 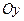 и аппликат –
и аппликат – 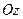 ) выберем одинаковый масштаб измерения. Вдоль положительного направления каждой оси отложим отрезки единичной длины. Обозначим орты осей:
) выберем одинаковый масштаб измерения. Вдоль положительного направления каждой оси отложим отрезки единичной длины. Обозначим орты осей: 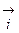 ,
,  – через
– через 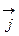 ,
, 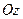 – через
– через 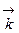 (рис. 8). Так как вектора
(рис. 8). Так как вектора 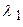 ,
, 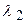 и
и 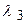 выступают проекции вектора на соответствующие оси:
выступают проекции вектора на соответствующие оси: 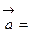
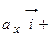
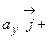
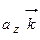 .
.
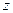
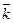
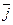
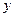
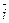
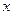
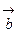 и
и 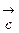 называется правой (левой), если обход векторов
называется правой (левой), если обход векторов 
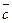 а)
а) 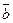
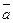
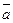
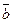
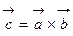 , который
, который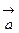 и
и 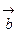 ;
;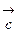 определяется по правилу правого винта: при вращении вектора
определяется по правилу правого винта: при вращении вектора 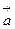 и
и 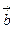 (рис. 10):
(рис. 10):
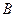
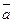
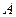

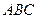 высота
высота 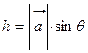 , тогда
, тогда 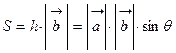 , следовательно, длина вектора
, следовательно, длина вектора 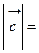
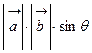 , где
, где 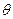 - угол между векторами
- угол между векторами 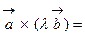
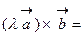
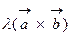 ; 2.
; 2. 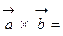
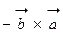 ; 3.
; 3. 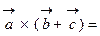
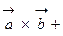
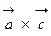 ;
; 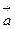 коллинеарен вектору
коллинеарен вектору 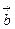 (
(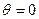 или
или  ), то их векторное произведение равно нулю:
), то их векторное произведение равно нулю: 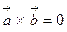 . Свойство 4 определяет второе условие коллинеарности векторов.
. Свойство 4 определяет второе условие коллинеарности векторов. 


