
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Величина транспонированного определителя равна величине исходного определителя.
2. Перестановка местами двух строк (столбцов) изменяет знак определителя на противоположный. 3. Определитель, содержащий две (или более) одинаковых строки (столбца), равен нулю. 4. Для того чтобы умножить определитель на число 5. Если две каких-либо строки (столбца) пропорциональны, то определитель равен нулю. 6. Если все элементы какой-либо строки (столбца) равны нулю, то опреде-литель равен нулю. 7. Если элементы какой-либо строки (столбца) можно представить в виде двух слагаемых, то сам определитель можно представить в виде суммы двух определителей. 8. Если все элементы какой-либо строки (столбца) умножить на вещественное число 9. (Метод раскрытия определителя по элементам какой-либо строки (столбца); универсальный способ вычисления определителя любого порядка). Определитель любого порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения: Пример 6. Вычислить определитель Воспользуемся свойством 9: раскроем определитель по элементам 3 строки
Вычислим определитель по элементам 2 столбца
Отсюда видно, что свойство 9 является универсальным методом вычисления определителя любого порядка по элементам любой строки или столбца. “Матрицы и действия с ними” О1. Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов: В дальнейшем будем писать матрицу в сокращенном виде О2. Если матрица содержит m строк и 1 столбец, то она называется матри-цей-столбцом О3. Если матрица содержит 1 строку и n столбцов, то она называется мат-рицей-строкой Пример 1. О4. Матрица, у которой совпадает количество строк с количеством столбцов, называется квадратной.
Пример 2. Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы О5. Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы – на соответствующие строки. Согласно свойству 1 для определителей для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы. О6. Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной О7. Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной О8. Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю:
Над матрицами можно выполнять следующие действия: 1. Суммой (разностью) двух матриц Пример 3. Найти сумму и разность матриц
Из приведенных матриц складывать (вычитать) можно только матрицы
и разность этих матриц
2. При умножении вещественного числа Пример 4. Умножить (-2) на матрицу Результат умножения имеет вид 3. Произведением матриц Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы. Пример 5. Найти (если это возможно) произведение матриц
Матрица
структуру результирующей матрицы: имеем размерности
Отсюда следует, что Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е. О9. Обратной матрицей к исходной квадратной матрице матрица Рассмотрим схему построения обратной матрицы – находят детерминант матрицы – вычисляют алгебраические дополнения – записывают выражение для обратной матрицы Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде. Пример 6. Найти обратную матрицу к матрице Вычислим детерминант данной матрицы
Вычислим алгебраические дополнения всех элементов данного определителя:
Запишем обратную матрицу
Таким образом, “Методы решения систем линейных алгебраических уравнений” Метод Крамера. О1. Системой линейных алгебраических уравнений (СЛАУ) называется выражение О2. Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы Крамер предложил следующий метод решения СЛАУ: умножим главный опре-делитель на Второй столбец умножим на
Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, то есть О3. Определитель Поступая аналогично найдем все вспомогательные определители СЛАУ:
Для того чтобы найти вспомогательный определитель О4. Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы: – если главный определитель системы отличен от нуля ( – если главный определитель системы равен нулю (
– если все определители системы равны нулю ( Пример 1. Решить СЛАУ методом Крамера Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Воспользуемся формулами Крамера
После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляются в нормализованную си-стему линейных алгебраических уравнений. Выполним проверку
|
|||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 63; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.107.149 (0.034 с.) |
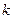 , достаточно умножить на это число все элементы какой-либо одной строки (столбца). Обратно: если все элементы какой-либо строки (столбца) имеют общий множитель
, достаточно умножить на это число все элементы какой-либо одной строки (столбца). Обратно: если все элементы какой-либо строки (столбца) имеют общий множитель 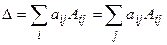 .
.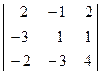 по элементам 3 строки и по элементам 2 столбца.
по элементам 3 строки и по элементам 2 столбца.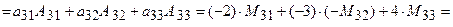
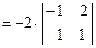
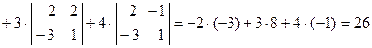 .
.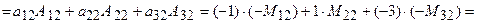
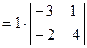
 .
. .
.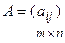 , где числа
, где числа 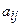 называются матричными элементами,
называются матричными элементами, 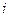 – нумератор строк,
– нумератор строк, 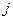 – нумератор столбцов, выражение
– нумератор столбцов, выражение 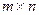 будем называть размерностью матрицы или ее структурой.
будем называть размерностью матрицы или ее структурой.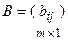 .
. .
. – матрица-столбец;
– матрица-столбец;  – матрица-строка.
– матрица-строка.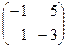 – квадратная матрица размерностью 2 х 2.
– квадратная матрица размерностью 2 х 2.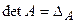 .
.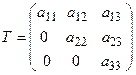 .
.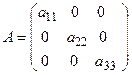 .
.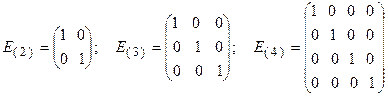 .
.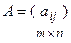 и
и 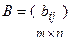 одинаковой структуры называется матрица той же размерности
одинаковой структуры называется матрица той же размерности  , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:  .
.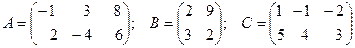 .
. и
и 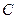 , которые имеют одинаковую структуру. Найдем сумму
, которые имеют одинаковую структуру. Найдем сумму
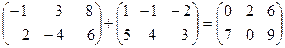
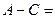
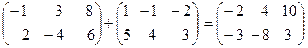 .
. на матрицу
на матрицу 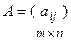 все элементы матрицы умножаются на это число.
все элементы матрицы умножаются на это число.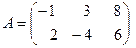 .
.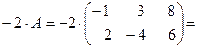
 .
.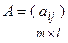 и
и 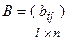 называется матрица
называется матрица 
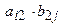
 .
.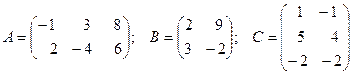 .
.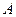 имеет структуру
имеет структуру  , матрица
, матрица  –
– 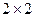 , матрица
, матрица 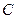 –
–  . Согласно определению можно найти произведения
. Согласно определению можно найти произведения 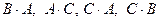 . Не существуют произведения
. Не существуют произведения  ,
, 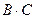 . Вычислим произведение
. Вычислим произведение 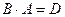 . Прежде всего, определим
. Прежде всего, определим и
и 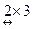 , убирая подчеркнутые цифры, получим структуру результирующей матрицы
, убирая подчеркнутые цифры, получим структуру результирующей матрицы  . Теперь вычислим ее элементы. Для того чтобы найти элементы результирующей матрицы, надо просуммировать произведения элементов выбранной строки первой матрицы на соответствующие элементы столбца второй матрицы:
. Теперь вычислим ее элементы. Для того чтобы найти элементы результирующей матрицы, надо просуммировать произведения элементов выбранной строки первой матрицы на соответствующие элементы столбца второй матрицы: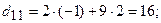
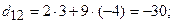

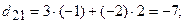
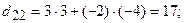
 .
.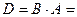

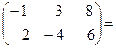
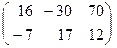 . Остальные возможные произведения найти самостоятельно.
. Остальные возможные произведения найти самостоятельно. .
. называется
называется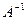 той же структуры, произведение которой с матрицей
той же структуры, произведение которой с матрицей 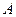 коммутативно и равно единичной матрице, то есть
коммутативно и равно единичной матрице, то есть 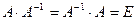 .
. :
: (
(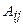 (см. «Определители») всех элементов определителя
(см. «Определители») всех элементов определителя  ;
;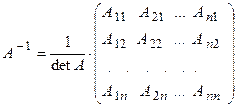 .
.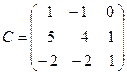 .
.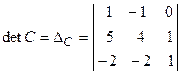 , раскроем этот определитель по элементам первой строки:
, раскроем этот определитель по элементам первой строки: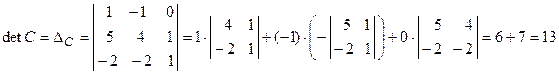 .
.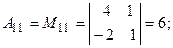
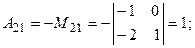
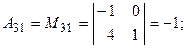

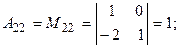

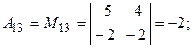

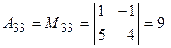 .
.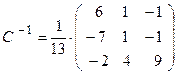 . Проверим правильность нахож-дения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
. Проверим правильность нахож-дения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы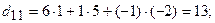
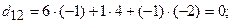

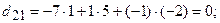
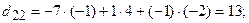
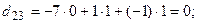
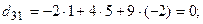

 .
.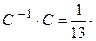
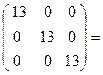

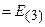 , то есть обратная матрица вычислена верно.
, то есть обратная матрица вычислена верно.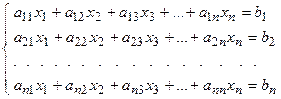 , где числа
, где числа 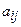 называются коэффициентами при неизвестных
называются коэффициентами при неизвестных 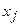 , а числа
, а числа 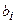 называются свободными коэффициентами.
называются свободными коэффициентами.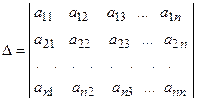 .
.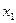 , для этого умножим все элементы первого столбца на эту неиз-вестную:
, для этого умножим все элементы первого столбца на эту неиз-вестную: 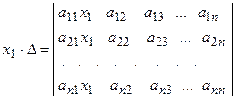 .
.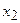 , третий столбец – на
, третий столбец – на 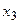 , …,
, …, 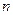 -ый столбец – на
-ый столбец – на 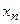 и все эти произведения прибавим к первому столбцу, при этом произведение
и все эти произведения прибавим к первому столбцу, при этом произведение 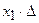 не изменится:
не изменится: 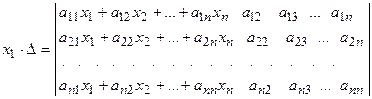 .
.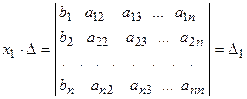 .
.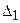 называется первым вспомогательным определителем СЛАУ.
называется первым вспомогательным определителем СЛАУ.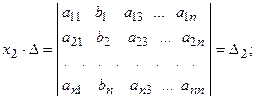
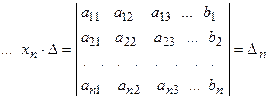 .
.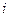 , надо в главном определителе СЛАУ заменить столбец
, надо в главном определителе СЛАУ заменить столбец 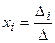 .
.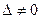 ), то система имеет единственное решение;
), то система имеет единственное решение;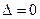 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля (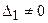 или
или 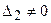 , или …, или
, или …, или 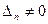 ), то система не имеет решений (деление на нуль запрещено(!!!));
), то система не имеет решений (деление на нуль запрещено(!!!));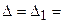
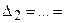
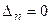 ), то система уравнений имеет бесчисленное множество решений.
), то система уравнений имеет бесчисленное множество решений.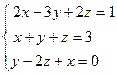 .
.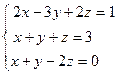 . Найдем главный определитель СЛАУ
. Найдем главный определитель СЛАУ 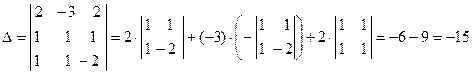 . Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
. Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя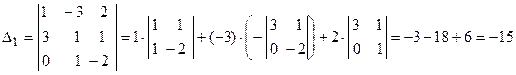 ;
;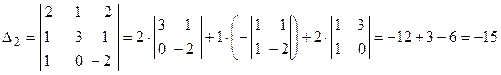 ;
; .
.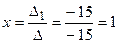 ;
; 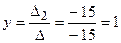 ;
; 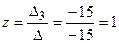 .
.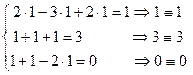 . Отсюда видно, что СЛАУ решена верно.
. Отсюда видно, что СЛАУ решена верно.


