
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Комплексная форма ряда Фурье.
Рассмотрим периодическую функцию В приложениях ряды Фурье часто применяются в комплексной форме. Преобразуем ряд Фурье и его коэффициенты, используя формулы Эйлера, выражающие синус и косинус через показательную функцию: Тогда получим:
Ряд Фурье принимает вид:
Замечание. В преобразованиях использованы формулы: Таким образом, формулу (1) можно записать в виде: Равенство (2) называется комплексной формой ряда Фурье. Если В электротехнике и радиотехнике члены указанного ряда называют гармониками, коэффициенты Пример. Построить ряд Фурье в комплексной форме для функции Решение. Запишем ряд Фурье в виде
В точках разрыва сумма ряда равна 4.1. Задачи для самостоятельного решения. Построить ряд Фурье в комплексной форме для следующих функций. 1. 2. 3. Тема 5. Интеграл Фурье. Преобразование Фурье. Если функция
Это разложение справедливо на всей числовой оси, если функция является периодической. Рассмотрим случай, когда функция Подставляя в ряд (1) коэффициенты (2) и (3), получим
Числа Будем неограниченно увеличивать
Поэтому, переходя в равенстве (5) к пределу при Формулу (6) можно записать в другом виде.
В формуле (7) видна аналогия интеграла Фурье с рядом Фурье. В обоих случаях функция раскладывается на сумму гармонических составляющих. Ряд Фурье суммируется по индексу «к», принимающему дискретные значения 1,2,3…. В интеграле Фурье ведется интегрирование по непрерывной переменной Замечания. 1) Если
2) Если
3) Если функция задана в интервале 4) Интеграл Фурье в комплексной форме имеет вид:
Пример. Представить интегралом Фурье функцию Решение. Данная функция имеет конечное число точек разрыва (х=0 и х=1). Она является абсолютно интегрируемой, так как отлична от нуля на конечном интервале. Поэтому существует несобственный интеграл
Подставим найденные коэффициенты в формулу Фурье.
Итак,
5.1. Преобразование Фурье. Формулу Фурье можно представить в симметричном виде, если положить Если
Преобразуем эту формулу следующим образом:
Обозначим В случае нечетной функции аналогично получим:
В комплексной форме имеем:
Пример. Найти прямое и обратное косинус - преобразование Фурье для функции Решение. Данная функция является абсолютно интегрируемой, т.к. задана на конечном интервале. Определим прямое косинус – преобразование Фурье.
Окончательно имеем Обратное косинус – преобразование Фурье:
5.1. Задачи для самостоятельного решения. 1) Представить интегралом Фурье функцию 2) Представить интегралом Фурье функцию 3) Представить интегралом Фурье функцию 4) Найти прямое и обратное косинус - преобразование Фурье для функции 5) Найти прямое и обратное косинус и синус- преобразование Фурье для функции Найти прямое косинус и синус- преобразование Фурье для функции
|
||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 43; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.131.238 (0.015 с.) |
 с периодом
с периодом  , удовлетворяющую условиям Дирихле. Ряд Фурье, составленный для этой функции, имеет вид
, удовлетворяющую условиям Дирихле. Ряд Фурье, составленный для этой функции, имеет вид 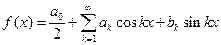 , где
, где 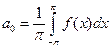 ,
, 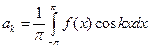 ,
,  .
.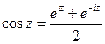 ,
,  .
.
 . Обозначим
. Обозначим 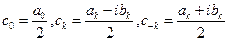 .
. (1). Определим комплексные коэффициенты этого ряда.
(1). Определим комплексные коэффициенты этого ряда.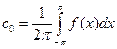 ,
,  ,
,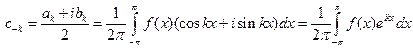 .
.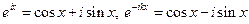 .
.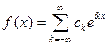 (2), где
(2), где  .
.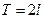 , то ряд Фурье в комплексной форме принимает вид:
, то ряд Фурье в комплексной форме принимает вид: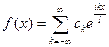 , где
, где 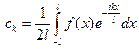 .
.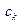 - комплексными амплитудами гармоник, а числа
- комплексными амплитудами гармоник, а числа  - волновыми числами функции
- волновыми числами функции 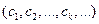 называется амплитудным спектром. Графически амплитудный спектр изображается в виде вертикальных отрезков длиной
называется амплитудным спектром. Графически амплитудный спектр изображается в виде вертикальных отрезков длиной  , расположенных в точках
, расположенных в точках  .
.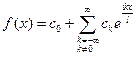 и определим его коэффициенты.
и определим его коэффициенты.  ,
,
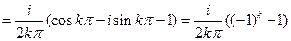 . Иначе,
. Иначе,  . С учетом полученных формул ряд Фурье в комплексной форме для заданной функции в точках непрерывности принимает вид:
. С учетом полученных формул ряд Фурье в комплексной форме для заданной функции в точках непрерывности принимает вид: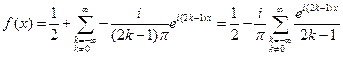 .
.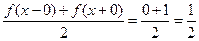 .
. ,
,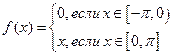 ,
,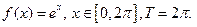
 условиям Дирихле, то ее можно представить рядом Фурье.
условиям Дирихле, то ее можно представить рядом Фурье.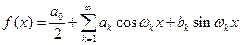 (1),где
(1),где  ,
,  (2),
(2), 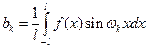 (3),
(3),  .
.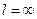 . Будем предполагать, что на любом конечном отрезке
. Будем предполагать, что на любом конечном отрезке  (4).
(4).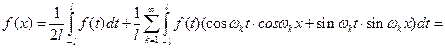
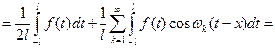
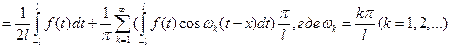 .(5)
.(5)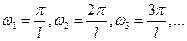 образуют арифметическую прогрессию, разность которой
образуют арифметическую прогрессию, разность которой  .
.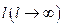 . Тогда первое слагаемое в формуле (5) стремится к нулю в силу равенства (4), а второе слагаемое напоминает интегральную сумму для функции
. Тогда первое слагаемое в формуле (5) стремится к нулю в силу равенства (4), а второе слагаемое напоминает интегральную сумму для функции . Предел этой суммы есть интеграл
. Предел этой суммы есть интеграл 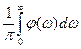 .
. , получим, что
, получим, что  , или
, или  (6). Формула (6) называется формулой Фурье, а интеграл в правой части формулы – интегралом Фурье. Формула Фурье справедлива в точках непрерывности функции
(6). Формула (6) называется формулой Фурье, а интеграл в правой части формулы – интегралом Фурье. Формула Фурье справедлива в точках непрерывности функции 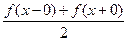 .
.
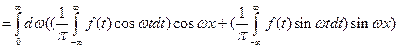 , или
, или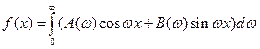 ,где
,где 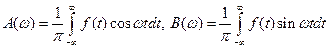 . (7)
. (7)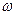 .
.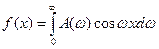 , где
, где  .
. , где
, где 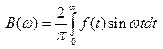 .
.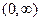 , то ее можно доопределить (продолжить) на интервал
, то ее можно доопределить (продолжить) на интервал 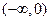 четным или нечетным образом.
четным или нечетным образом. , или
, или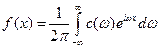 , где
, где 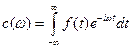 .
.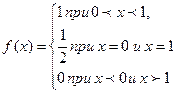
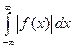 . Следовательно, данную функцию можно представить интегралом Фурье.
. Следовательно, данную функцию можно представить интегралом Фурье. ,
,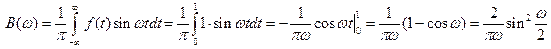 .
.
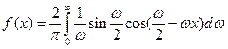 .
. .
. (2)
(2)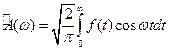 (3). Выражение (3) называется прямым косинус - преобразованием Фурье. Подставляя выражение (3) в формулу (2), получим обратное косинус - преобразование Фурье:
(3). Выражение (3) называется прямым косинус - преобразованием Фурье. Подставляя выражение (3) в формулу (2), получим обратное косинус - преобразование Фурье: 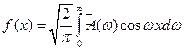 .
.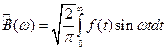 - прямое синус - преобразованием Фурье.
- прямое синус - преобразованием Фурье.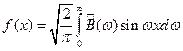 - обратное синус - преобразованием Фурье.
- обратное синус - преобразованием Фурье. - прямое преобразованием Фурье.
- прямое преобразованием Фурье. - обратное преобразованием Фурье.
- обратное преобразованием Фурье.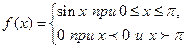 .
.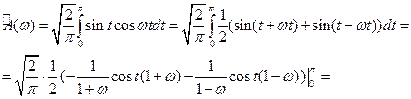
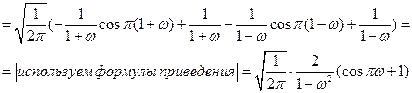
 .
.
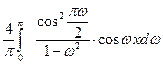 .
. , доопределив ее четным (нечетным) образом для отрицательных значений
, доопределив ее четным (нечетным) образом для отрицательных значений 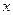 .
.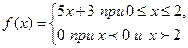
 , доопределив ее четным (нечетным) образом для отрицательных значений
, доопределив ее четным (нечетным) образом для отрицательных значений 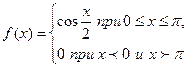 .
. .
.



