
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Специальные разделы математикиСтр 1 из 9Следующая ⇒
Н.Н. Авдеева, А.И. Руденко
ВЫСШАЯ МАТЕМАТИКА. СПЕЦИАЛЬНЫЕ РАЗДЕЛЫ МАТЕМАТИКИ Учебное пособие для курсантов, обучающихся по специальностям: 160905 «Техническая эксплуатация транспортного радиооборудования», 180405 «Эксплуатация судовых и энергетических установок», и направлению 14200 «Холодильная, криогенная техника и системы жизнеобеспечения» очной и заочной форм обучения
Калининград Издательство БГАРФ 2015 УДК 517.5 (07) Авторы: Авдеева Н.Н., канд. пед. наук, доцент Руденко А.И.,канд. физмат. наук.
В учебном пособии приведен обзор основных понятий и положений дисциплины «Специальные разделы математики», даны методические рекомендации по их изучению, выделены типовые задачи с решениями, представлены контрольные вопросы для самопроверки и задачи для самоподготовки по данной дисциплине, приведены варианты контрольных заданий для курсантов и студентов заочной формы обучения.
Печатается по решению редакционно-издательского совета Балтийской государственной академии рыбопромыслового флота
Рецензенты: Антипов Ю.Н., доктор физмат. наук, профессор, заведующий кафедрой высшей математики Калининградского технического университета; Зайцев А.И., канд. физмат. наук, зав. лабораторией математических методов защиты и обработки информации БФУ им. И. Канта.
© «БГАРФ» ФГБОУ ВПО «КГТУ», 2015 Введение. Тема 1. Комплексные числа. 1.1. Основные понятия. 1.2. Геометрическое изображение комплексных чисел. 1.3. Формы записи комплексного числа. 1.4. Действия над комплексными числами. 1.5. Вопросы для самопроверки. Тема 2. Функции комплексного переменного. 2.1. Основные определения. 2.2. Элементарные функции комплексного переменного. 2.3. Понятие предела и непрерывности функции комплексного переменного в точке. 2.4. Дифференцирование функции комплексного переменного. Условия Эйлера – Даламбера. 2.5. Задачи для самостоятельного решения. 2.6. Интегрирование функции комплексного переменного. 2.7. Вопросы для самопроверки. 2.8. Задачи для самостоятельного решения. 2.9. Особые точки. 2.10. Вычеты. 2.11. Задачи для самостоятельного решения. Тема3. Операционное исчисление. 3.1. Преобразование Лапласа. Оригиналы и их изображения.
3.2.Свойства преобразования Лапласа. 3.3. Таблица оригиналов и изображений. 3.4. Нахождение оригиналов по заданным изображениям в простейших случаях. 3.5. Задачи для самостоятельного решения. 3.6. Решение линейных дифференциальных уравнений с постоянными коэффициентами и систем линейных дифференциальных уравнений. 3.7. Передаточная функция. 3.8. Вопросы для самопроверки. 3.9. Задачи для самостоятельного решения. Тема 4. Комплексная форма ряда Фурье. 4.1. Задачи для самостоятельного решения. Тема 5. Интеграл Фурье. Преобразование Фурье. 5.1. Преобразование Фурье. 5.1. Задачи для самостоятельного решения. Тема 6. Элементы теории графов. 6.1. Основные определения. 6.2. Задачи для самостоятельного решения. Тема 7. Задачи для контрольных заданий.студентов заочной формы обучения 7.1 Решение типовых задач. Общий перечень рекомендуемой литературы. Основная литература. Дополнительная учебная литература.
Введение Настоящее пособие и контрольные задания составлены в соответствии с рабочей программой дисциплины «Высшая математика» на основании: - примерной программы дисциплины «Математика» для направления 550000 («Технические науки». Министерство образования Российской Федерации. – М., 2000); - учебного плана по специальностям: 160905 «Техническая эксплуатация транспортного радиооборудования»,180405 «Эксплуатация судовых и энергетических установок», 141 200 «Холодильная, криогенная техника и системы жизнеобеспечения» очной и заочной форм обучения. В результате изучения специальных разделов математики студент должен: знать основные базовые понятия и методы теории комплексных чисел, функции комплексного переменного, операционного исчисления; уметь применять теоретические знания для исследования простейших радиотехнических схем, систем и процессов; иметь опыт: - употребления математической символики для выражения количественных и качественных отношений объектов; - аналитического и численного решения уравнений, содержащих комплексные числа; - исследования аналитического и численного решения дифференциальных уравнений операционным методом;
- перевода технической задачи на математический язык; - составления математической модели физических и технических процессов; - использования справочной математической и технической литературы.
Тема 1. Комплексные числа. Основные понятия. Геометрическое изображение комплексных чисел. Формы записи комплексного числа. Действия над комплексными числами. Основные понятия. Понятие о мнимой единице возникло в связи с решением уравнения Полученному значению нельзя поставить в соответствие никакое действительное число. В середине 18 столетия Леонардом Эйлером был введен символ
Мнимой единицей Важно знать значения натуральных степеней числа
Заметим, что результаты возведения числа Комплексным числом Если Два комплексных числа равны, если равны их действительные и мнимые части. Соотношения «больше», «меньше» для комплексных чисел не определены. Два комплексных числа Вопросы для самопроверки. 1) Как определяется число 2) Какие числа называются комплексными? 3) Как комплексные числа изображаются на комплексной плоскости? Что называется модулем и аргументом комплексного числа? 4) Как записать комплексное число в алгебраической, тригонометрической и показательной формах? 5) Как выполняется сложение, вычитание, умножение, деление комплексных чисел? 6) Запишите формулу Муавра. 7) Как извлекается корень из комплексного числа? Сколько значений он имеет?
Степенная функция. Определение этой функции введем в соответствии с действиями возведения в натуральную степень комплексного числа и извлечения корня из комплексного числа, рассмотренными выше. Случай, когда На основании формулы Муавра Степенной функции с дробным показателем можно придать следующий вид Отметим, что функция 2. Показательная функция. Запишем известные разложения функций
Разложим в ряд функцию Применяя свойства степеней числа Видим, что в первой скобке получилось разложение Эта формула называется формулой Эйлера. Применим формально формулу Эйлера к функции Полученная формула принимается за определение показательной функции в комплексной области. Важно отметить, что при таком определении показательной функции остаются справедливыми известные правила умножения, деления, возведения в степень. Однако приобретается новое свойство периодичности. Действительно,
Из последнего следует, что показательная функция на комплексной плоскости является периодической с периодом Формула Эйлера позволяет любое комплексное число записать в показательной форме Пример 1.Доказать справедливость равенства Решение. Пример 2. Найти действительную и мнимую часть функции Решение. Действительная часть данной функции
Тригонометрические функции. Если формально применить формулу Эйлера к функциям Из этих равенств выразим Полученные формулы тоже называются формулами Эйлера. Правые части этих формул при комплексных значениях z принимают за определения функций
Отметим, что многие свойства тригонометрических функций, в частности все тождественные равенства, справедливы для комплексных значений
Гиперболические функции. В преобразованиях различных выражений, содержащих показательные функции, и во многих практических приложениях применяются так называемые гиперболические функции Приведем их определение. Гиперболический синус Гиперболический косинус Гиперболический тангенс Гиперболический котангенс Часто гиперболические функции удобно выражать через тригонометрические функции и наоборот. 5. Логарифмическая функция. Логарифмическая функция определяется как функция, обратная показательной. Число Обозначим Запишем число Два комплексных числа равны, если их модули равны, а аргументы могут отличаться на число, кратное
Пример. Найти Решение. Найдем модуль и аргумент числа
Вопросы для самопроверки. 1. Дайте определение области на комплексной плоскости. Какая точка называется граничной? Как определяется граница области?
2. Дайте определение степенной функции на комплексной плоскости. 3. Как определяется показательная функция на комплексной плоскости? Сохраняются ли ее свойства? Какое новое свойство она приобретает? Выведите формулу Эйлера. Запишите комплексное число в показательной форме. 4. Как определяются тригонометрические функции 5. Дайте определение логарифмической функции на комплексной плоскости. 6. Сформулируйте определения предела и непрерывности функции комплексного переменного в точке. 7. Дайте определение производной функции комплексного переменного. Какая функция называется аналитической? Выведите необходимые и достаточные условия аналитичности функции. 8. Как определяется интеграл от функции комплексного переменного? 9. Сформулируйте теоремы Коши для односвязной и многосвязной области и следствия из них. 10. Как применяется формула Коши для вычисления некоторых интегралов? 2.8. Задачи для самостоятельного решения. 1) Вычислить интеграл 2) Вычислить интеграл 3) Вычислить интеграл 4) Вычислить по формуле Коши: а) б) г)
2.9. Особые точки. Определение. Точки, в которых нарушается аналитичность функции, называются особыми. Точка Отметим, что это определение справедливо только для односвязной области. Различают три типа изолированных особых точек. 1) Точка 2) Полюсом порядка К называется такая изолированная особая точка 3) Точка Пример 1.
Пример 2. Пример 3. Задачи для самостоятельного решения. Установить вид особых точек для следующих функций: 1) Вычеты. Понятие вычета является одним из важнейших понятий теории функций комплексного переменного. Если функция
Определение. Вычетом функции Обозначается вычет:
Теорема 1. Вычет функции Доказательство. Пусть точкой. Доопределим функцию
Теорема 2. Если функция Доказательство. По определению простого полюса
Пример. Найти вычет функции Решение. Заданная точка является простым полюсом. Поэтому
Теорема 3. Если функция Например, для полюса второго порядка эта формула принимает вид: Для полюса третьего порядка Пример. Найти вычет функции
Решение.
Найдем производную второго порядка данной функции.
С учетом этого результата получим:
Теорема 5. Основная теорема о вычетах. (Коши, 1825г.). Если функция Доказательство. По теореме Коши для многосвязной области
Пример.Вычислить Решение. Подынтегральная функция имеет две особые точки: 1)
2) 3) 2.11. Задачи для самостоятельного решения. 1) Определить вычеты функции относительно ее особых точек: а) г) 2) С помощью вычетов вычислить интегралы: а) б) в) г) д) е)
Свойство линейности. Если Свойство вытекает из основных свойств интеграла. Оно говорит о том, что изображение суммы нескольких слагаемых равно сумме изображений отдельных слагаемых, при этом постоянный множитель можно выносить за знак изображения. Пример.Пользуясь свойством линейности, найти изображение функции Решение. 2. Теорема подобия. Если Доказательство. По определению имеем Заменим
Пример.Найти изображение функции Решение.Мы показали, что
3. Теорема запаздывания (оригинала). Если Доказательство. Найдем изображение функции Первый интеграл равен нулю, так как
Пример.Найти изображение функций Решение. Теорему запаздывания удобно применять при отыскании изображений функций, заданных несколькими аналитическими выражениями. Функция С помощью этой функции запаздывающую функцию можно представить в виде: Пример. Найти изображение функции Решение. Данная функция равна нулю при Пример. Найти изображение функции Решение. Функция, Чтобы найти изображение этой функции с помощью теоремы запаздывания, ее нужно представить в виде:
Имеем: Так как
Теорема смещения (изображения). Если Пример. 3. Дифференцирование оригинала. Если Доказательство. Докажем первое соотношение. По определению изображения находим
4. Дифференцирование изображения. Если
5. Интегрирование оригинала. Если функция
6. Интегрирование изображения. Если
Таблица оригиналов и изображений. Составим краткую таблицу, устанавливающую соответствие между часто встречающимися на практике оригиналами и их изображениями. Таблица оригиналов и изображений.
|
|||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 61; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.169 с.) |

 для обозначения
для обозначения  .
.  ,
,  .
. называется число, квадрат которого равен -1.
называется число, квадрат которого равен -1.


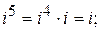
 и т.д.
и т.д.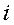 в натуральную степень периодически повторяются. Периодом является число 4.
в натуральную степень периодически повторяются. Периодом является число 4. называется выражение вида,
называется выражение вида, 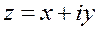 где
где  и
и 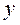 действительные числа,
действительные числа, 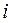 – мнимая единица.
– мнимая единица.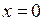 , то число
, то число 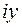 называется чисто мнимым; если
называется чисто мнимым; если  , то
, то 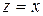 - действительное число. Это значит, что действительные числа являются подмножеством комплексных чисел. Число
- действительное число. Это значит, что действительные числа являются подмножеством комплексных чисел. Число 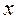 называется действительной частью комплексного числа и обозначается
называется действительной частью комплексного числа и обозначается 
 – мнимая часть, обозначается
– мнимая часть, обозначается 
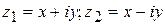 , различающиеся знаком мнимой части, называются сопряженными.
, различающиеся знаком мнимой части, называются сопряженными.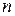 – целое отрицательное число, не рассматриваем.
– целое отрицательное число, не рассматриваем. степенной функции можно придать следующий вид
степенной функции можно придать следующий вид
 ,где
,где 
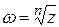 является многозначной.
является многозначной. в степенной ряд для действительных значений x.
в степенной ряд для действительных значений x.

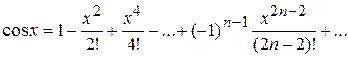
 , пользуясь формально разложением
, пользуясь формально разложением 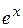 .
.
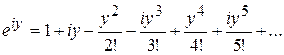 , или
, или
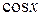 в степенной ряд, а во второй – разложение
в степенной ряд, а во второй – разложение  . Полученному результату можно придать следующий вид:
. Полученному результату можно придать следующий вид: .
.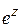 .
.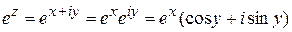 , т. е.
, т. е.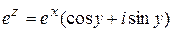 .
. .
. , так как
, так как  .
.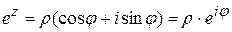 .
. .
.
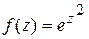 .
.
 , мнимая часть –
, мнимая часть – 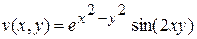 .
. и
и  , т.е. заменить в ней
, т.е. заменить в ней  на
на 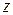 и
и  , то получим
, то получим 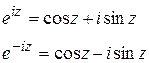
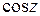 и
и 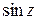 .
.  ,
, 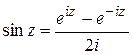 .
.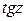 и
и 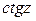 определяются по формулам
определяются по формулам

 . Если учесть, что
. Если учесть, что  , то
, то 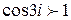 .
.
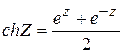

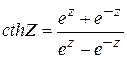

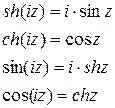
 называется логарифмом числа
называется логарифмом числа  и обозначается
и обозначается 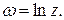
 Тогда
Тогда  .
.
 Следовательно,
Следовательно, 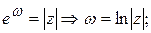
 , где
, где 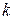 – любое целое число. В результате получим:
– любое целое число. В результате получим: .
.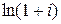 .
.
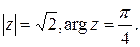
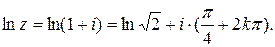
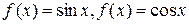 на комплексной плоскости?
на комплексной плоскости?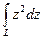 , если контур
, если контур 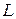 –а) ломаная
–а) ломаная  с вершинами в точках
с вершинами в точках 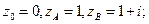 б) отрезок, соединяющий точки
б) отрезок, соединяющий точки 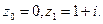
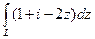 , если контур
, если контур 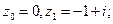 б) часть параболы
б) часть параболы  , соединяющей эти точки.
, соединяющей эти точки. , если контур
, если контур 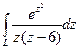 , если
, если 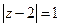 , б)
, б) 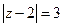 ,
,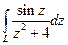 , если
, если 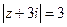 , в)
, в)  , если
, если  ,
,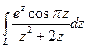 , если
, если 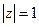 .
.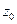 называется изолированной особой точкой, если существует окрестность этой точки, в которой функция является аналитической, за исключением самой точки.
называется изолированной особой точкой, если существует окрестность этой точки, в которой функция является аналитической, за исключением самой точки.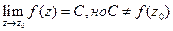 .
. . Если
. Если 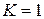 , полюс называется простым.
, полюс называется простым.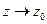 функция
функция 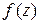 не имеет предела (ни конечного, ни бесконечного).
не имеет предела (ни конечного, ни бесконечного).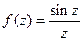 . Точка
. Точка 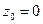 является устранимой особой точкой, т.к.
является устранимой особой точкой, т.к. .
. 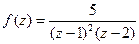 . Точка
. Точка 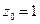 является полюсом второго порядка, а точка
является полюсом второго порядка, а точка 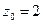 является простым полюсом.
является простым полюсом. . Точка
. Точка  а
а 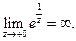
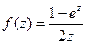 ; 2)
; 2)  ; 3)
; 3)  .
.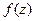 является аналитической в односвязной области, то
является аналитической в односвязной области, то 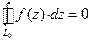 , где
, где 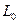 - любой замкнутый контур, лежащий в этой области. Если внутри контура
- любой замкнутый контур, лежащий в этой области. Если внутри контура  , называть вычетом.
, называть вычетом.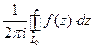 , где
, где 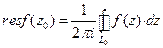 .
.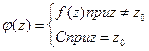 . Тогда по теореме Коши
. Тогда по теореме Коши  . На контуре
. На контуре 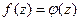 . Поэтому и
. Поэтому и 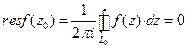 .
. .
.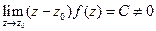 . Отсюда следует, что в окрестности точки
. Отсюда следует, что в окрестности точки 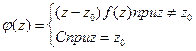 является аналитической. По теореме Коши имеем
является аналитической. По теореме Коши имеем  . Принимая во внимание то, что на контуре
. Принимая во внимание то, что на контуре  , получим
, получим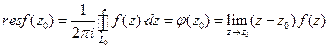 .
.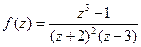 относительно особой точки
относительно особой точки  .
. .
.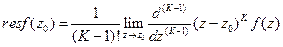 .
.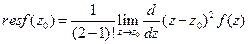 .
. .
.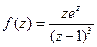 относительно точки
относительно точки 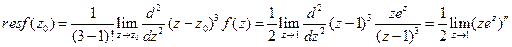 .
.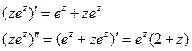 .
.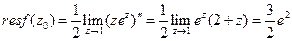 .
.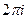 на сумму вычетов относительно особых точек, лежащих внутри контура L.
на сумму вычетов относительно особых точек, лежащих внутри контура L.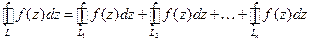 , где
, где  - особые точки,
- особые точки,  - окружности достаточно малых радиусов с центрами в этих точках. Применяя определение вычетов, каждый интеграл правой части можно заменить произведением
- окружности достаточно малых радиусов с центрами в этих точках. Применяя определение вычетов, каждый интеграл правой части можно заменить произведением 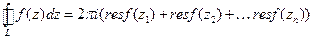 .
. , где L – окружность
, где L – окружность 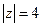 .
.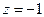 - полюс 2 порядка и
- полюс 2 порядка и  - простой полюс. По основной теореме о вычетах имеем:
- простой полюс. По основной теореме о вычетах имеем: 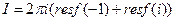 .
.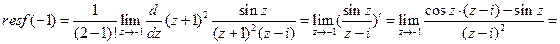
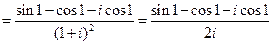 .
.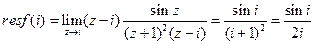 .
. .
. ; б)
; б) 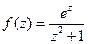 ;
;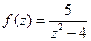 ; д)
; д) 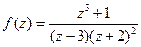 .
. , где L:
, где L: 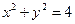 ,
,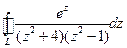 , где L:
, где L:  ,
,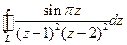 , где L:
, где L: 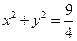 ,
, , где L:
, где L: 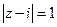 ,
,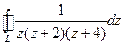 , где L:
, где L: 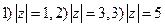 ,
,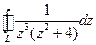 , где L:
, где L:  .
.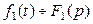 и
и 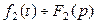 , то при любых комплексных постоянных
, то при любых комплексных постоянных 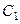 и
и 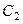 справедливо соотношение
справедливо соотношение 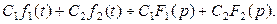
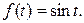
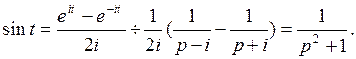
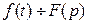 , то для любого постоянного
, то для любого постоянного 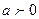 справедливо соотношение:
справедливо соотношение: 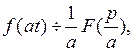 т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число.
т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число.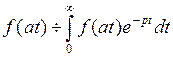 .
.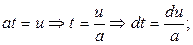 при t =0 u =0, при
при t =0 u =0, при 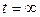
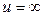 . Следовательно,
. Следовательно,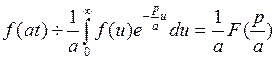 , что и требовалось доказать.
, что и требовалось доказать. .
.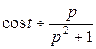 . По теореме подобия имеем
. По теореме подобия имеем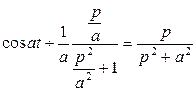 .
.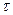 справедливо соотношение
справедливо соотношение 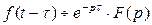 , т.е. запаздывание оригинала на положительную величину
, т.е. запаздывание оригинала на положительную величину 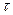 приводит к умножению изображения функции
приводит к умножению изображения функции 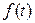 на величину
на величину 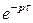 .
.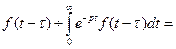
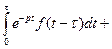
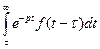 .
.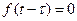 при
при 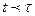 , во втором интеграле сделаем замену переменной.
, во втором интеграле сделаем замену переменной.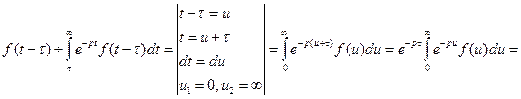
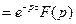 , что и требовалось доказать.
, что и требовалось доказать.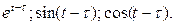
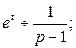
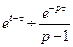 ;
; 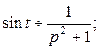
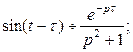
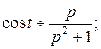
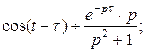
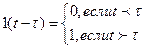 называется обобщенной единичной функцией. Так как
называется обобщенной единичной функцией. Так как  , то
, то  .
.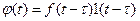 .
.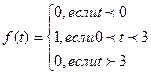 .
.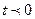 . В момент времени
. В момент времени 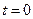 «включается» функция, равная 1, а в момент
«включается» функция, равная 1, а в момент 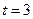 она «снимается». С помощью единичной функции можно записать:
она «снимается». С помощью единичной функции можно записать: 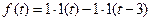
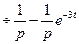 .
.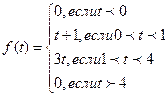
 .
.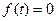 при
при 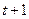 , а в момент
, а в момент 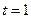 она «снимается» и «включается» функция
она «снимается» и «включается» функция 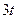 , которая «снимается» в момент
, которая «снимается» в момент 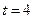 . Поэтому
. Поэтому 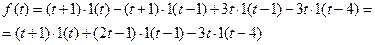 .
.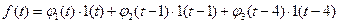 .
.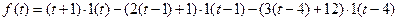 .
.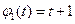
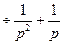 ,
,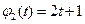
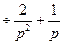 ,
,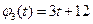
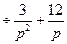 , то, применяя теорему запаздывания, получим искомое изображение:
, то, применяя теорему запаздывания, получим искомое изображение: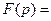
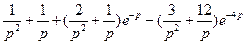 .
.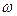 имеет место соотношение
имеет место соотношение 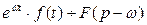 .
.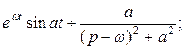
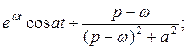
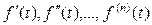 являются оригиналами, то
являются оригиналами, то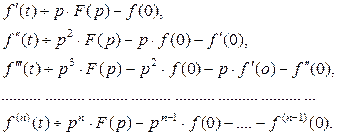
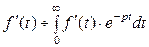 . По формуле интегрирования по частям, обозначив
. По формуле интегрирования по частям, обозначив 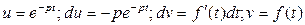 , получим
, получим 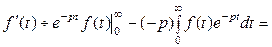
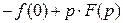 , что и требовалось доказать.
, что и требовалось доказать.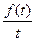 , то
, то 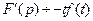 ;
;  ;
; 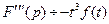 .
.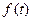 непрерывна при всех значениях
непрерывна при всех значениях 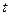 в интервале
в интервале 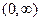 и
и 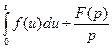 .
.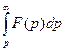 сходится, то он служит изображением функции
сходится, то он служит изображением функции 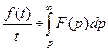 .
.


