
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема3. Операционное исчисление.
Преобразование Лапласа. Оригиналы и их изображения. Свойства преобразования Лапласа. Таблица оригиналов и изображений. Нахождение оригиналов по заданным изображениям в простейших случаях. Решение линейных дифференциальных уравнений с постоянными коэффициентами и систем дифференциальных уравнений. Методы операционного исчисления с успехом применяются в инженерной практике при изучении переходных явлений в электрических цепях, в расчетах различных систем автоматического регулирования процессов и т. д. Правила операционного исчисления созданы английским инженером – электриком О. Хевисайдом (1850-1925) без достаточно строгого математического обоснования. Однако эти правила позволили легкими и эффективными приемами находить решение дифференциальных уравнений, которые получались при изучении явлений в различных областях техники. В настоящее время операционное исчисление является самостоятельной отраслью математического анализа. Методы операционного исчисления предполагают следующую схему решения задач. Допустим, что необходимо найти решение заданного дифференциального уравнения. 1. От искомых функций переходят к некоторым другим функциям – их изображениям. Определяют изображения всех составляющих данного уравнения 2. Составляют вспомогательное, так называемое операторное, уравнение, из которого легко находят изображение неизвестной функции. 3. Получив результат при действиях над изображениями, возвращаются к самим функциям. Хорошей аналогией с операционным исчислением может служить применение логарифмов к вычислению значений выражений. В качестве преобразования, позволяющего перейти от функции к ее изображению, будем применять преобразование Лапласа. 3.1. Преобразование Лапласа. Оригиналы и их изображения. Пусть Функция
Определение. Функцией – оригиналом называется функция 1) 2) при 3) при Требования, предъявляемые к функции Для оригинала и изображения будем применять сокращенные обозначения:
Можно показать, что интеграл Лапласа сходится абсолютно для всех значений комплексной переменной Пример.Найти изображение показательной функции Решение. Данная функция является оригиналом. По определению
если Таким образом, Пример. Найти изображение единичной функции Решение. Данная функция является оригиналом. Поэтому
Таким образом, Пример. Найти изображение функции Решение. Данная функция является оригиналом. Поэтому
3.2.Свойства преобразования Лапласа. Свойство линейности. Если Свойство вытекает из основных свойств интеграла. Оно говорит о том, что изображение суммы нескольких слагаемых равно сумме изображений отдельных слагаемых, при этом постоянный множитель можно выносить за знак изображения. Пример.Пользуясь свойством линейности, найти изображение функции Решение. 2. Теорема подобия. Если
Доказательство. По определению имеем Заменим
Пример.Найти изображение функции Решение.Мы показали, что
3. Теорема запаздывания (оригинала). Если Доказательство. Найдем изображение функции Первый интеграл равен нулю, так как
Пример.Найти изображение функций Решение. Теорему запаздывания удобно применять при отыскании изображений функций, заданных несколькими аналитическими выражениями. Функция С помощью этой функции запаздывающую функцию можно представить в виде: Пример. Найти изображение функции Решение. Данная функция равна нулю при Пример. Найти изображение функции Решение. Функция, Чтобы найти изображение этой функции с помощью теоремы запаздывания, ее нужно представить в виде:
Имеем: Так как
Теорема смещения (изображения). Если Пример. 3. Дифференцирование оригинала. Если Доказательство. Докажем первое соотношение. По определению изображения находим
4. Дифференцирование изображения. Если
5. Интегрирование оригинала. Если функция
6. Интегрирование изображения. Если
Таблица оригиналов и изображений. Составим краткую таблицу, устанавливающую соответствие между часто встречающимися на практике оригиналами и их изображениями. Таблица оригиналов и изображений.
|
||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 41; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.243 (0.029 с.) |
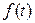 - действительная функция действительного переменного. Поставим ей в соответствие функцию комплексной переменной
- действительная функция действительного переменного. Поставим ей в соответствие функцию комплексной переменной 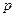 следующим образом
следующим образом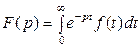 (1)
(1)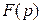 называется изображением функции
называется изображением функции  при
при 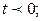
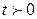 функция
функция 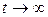 функция
функция 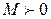 и
и 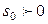 , что для всех t будет выполняться неравенство
, что для всех t будет выполняться неравенство 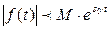 . Это значит, что модуль функции
. Это значит, что модуль функции 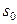 называется показателем роста функции. Если
называется показателем роста функции. Если 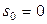 , функция называется ограниченной.
, функция называется ограниченной.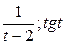 и др.
и др.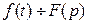 (
(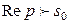 , где
, где 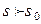 .
.
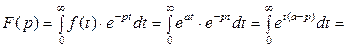
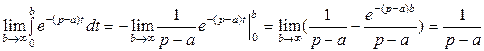 ,
,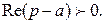
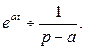
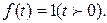
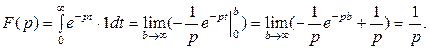
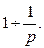
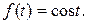
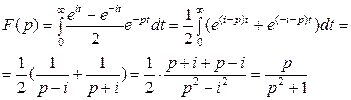
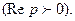
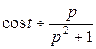 .
.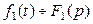 и
и 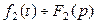 , то при любых комплексных постоянных
, то при любых комплексных постоянных 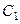 и
и 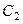 справедливо соотношение
справедливо соотношение 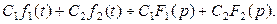
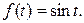
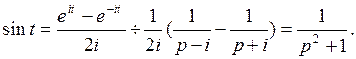
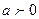 справедливо соотношение:
справедливо соотношение: 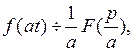 т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число.
т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число.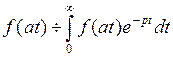 .
.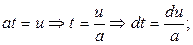 при t =0 u =0, при
при t =0 u =0, при 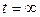
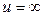 . Следовательно,
. Следовательно,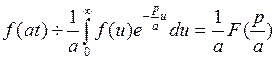 , что и требовалось доказать.
, что и требовалось доказать. .
.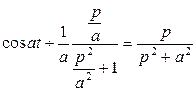 .
.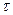 справедливо соотношение
справедливо соотношение 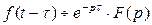 , т.е. запаздывание оригинала на положительную величину
, т.е. запаздывание оригинала на положительную величину 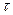 приводит к умножению изображения функции
приводит к умножению изображения функции 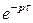 .
.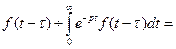
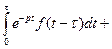
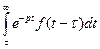 .
.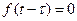 при
при 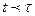 , во втором интеграле сделаем замену переменной.
, во втором интеграле сделаем замену переменной.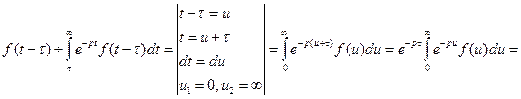
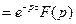 , что и требовалось доказать.
, что и требовалось доказать.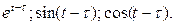
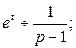
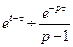 ;
; 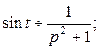
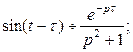
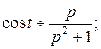
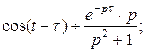
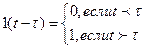 называется обобщенной единичной функцией. Так как
называется обобщенной единичной функцией. Так как  , то
, то  .
.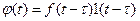 .
.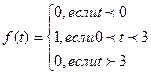 .
.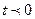 . В момент времени
. В момент времени 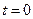 «включается» функция, равная 1, а в момент
«включается» функция, равная 1, а в момент 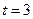 она «снимается». С помощью единичной функции можно записать:
она «снимается». С помощью единичной функции можно записать: 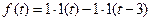
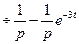 .
.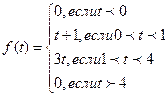
 .
.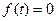 при
при 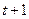 , а в момент
, а в момент 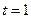 она «снимается» и «включается» функция
она «снимается» и «включается» функция 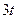 , которая «снимается» в момент
, которая «снимается» в момент 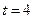 . Поэтому
. Поэтому 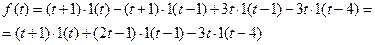 .
.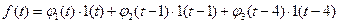 .
.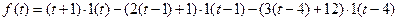 .
.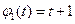
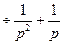 ,
,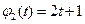
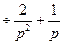 ,
,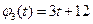
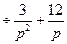 , то, применяя теорему запаздывания, получим искомое изображение:
, то, применяя теорему запаздывания, получим искомое изображение: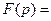
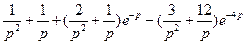 .
.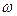 имеет место соотношение
имеет место соотношение 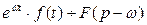 .
.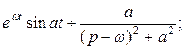
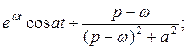
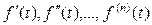 являются оригиналами, то
являются оригиналами, то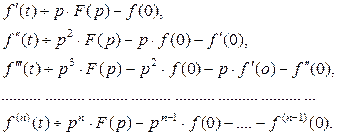
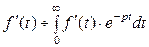 . По формуле интегрирования по частям, обозначив
. По формуле интегрирования по частям, обозначив 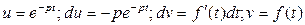 , получим
, получим 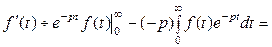
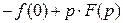 , что и требовалось доказать.
, что и требовалось доказать.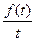 , то
, то 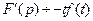 ;
;  ;
; 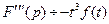 .
.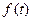 непрерывна при всех значениях
непрерывна при всех значениях 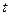 в интервале
в интервале 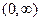 и
и 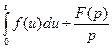 .
.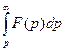 сходится, то он служит изображением функции
сходится, то он служит изображением функции 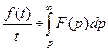 .
.


