Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарные функции комплексного переменного.
Элементарные функции комплексного переменного являются естественным распространением на комплексную плоскость элементарных функций действительного переменного. Однако все эти функции в комплексной области требуют своего определения и обладают некоторыми своеобразными свойствами. Степенная функция. Определение этой функции введем в соответствии с действиями возведения в натуральную степень комплексного числа и извлечения корня из комплексного числа, рассмотренными выше. Случай, когда На основании формулы Муавра Степенной функции с дробным показателем можно придать следующий вид Отметим, что функция 2. Показательная функция. Запишем известные разложения функций
Разложим в ряд функцию Применяя свойства степеней числа Видим, что в первой скобке получилось разложение Эта формула называется формулой Эйлера. Применим формально формулу Эйлера к функции Полученная формула принимается за определение показательной функции в комплексной области. Важно отметить, что при таком определении показательной функции остаются справедливыми известные правила умножения, деления, возведения в степень. Однако приобретается новое свойство периодичности. Действительно, Из последнего следует, что показательная функция на комплексной плоскости является периодической с периодом Формула Эйлера позволяет любое комплексное число записать в показательной форме Пример 1.Доказать справедливость равенства Решение. Пример 2. Найти действительную и мнимую часть функции Решение. Действительная часть данной функции
Тригонометрические функции. Если формально применить формулу Эйлера к функциям Из этих равенств выразим
Полученные формулы тоже называются формулами Эйлера. Правые части этих формул при комплексных значениях z принимают за определения функций
Отметим, что многие свойства тригонометрических функций, в частности все тождественные равенства, справедливы для комплексных значений
Гиперболические функции. В преобразованиях различных выражений, содержащих показательные функции, и во многих практических приложениях применяются так называемые гиперболические функции Приведем их определение. Гиперболический синус Гиперболический косинус Гиперболический тангенс Гиперболический котангенс Часто гиперболические функции удобно выражать через тригонометрические функции и наоборот. 5. Логарифмическая функция. Логарифмическая функция определяется как функция, обратная показательной. Число Обозначим Запишем число Два комплексных числа равны, если их модули равны, а аргументы могут отличаться на число, кратное
Пример. Найти Решение. Найдем модуль и аргумент числа
|
|||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 40; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.132 (0.008 с.) |
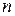 – целое отрицательное число, не рассматриваем.
– целое отрицательное число, не рассматриваем. степенной функции можно придать следующий вид
степенной функции можно придать следующий вид
 ,где
,где 
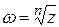 является многозначной.
является многозначной. в степенной ряд для действительных значений x.
в степенной ряд для действительных значений x.

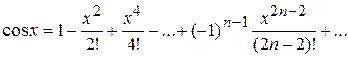
 , пользуясь формально разложением
, пользуясь формально разложением 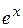 .
.
 , получим
, получим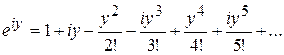 , или
, или
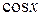 в степенной ряд, а во второй – разложение
в степенной ряд, а во второй – разложение  . Полученному результату можно придать следующий вид:
. Полученному результату можно придать следующий вид: .
.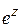 .
.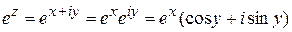 , т. е.
, т. е.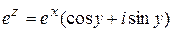 .
. .
. , так как
, так как  .
.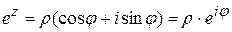 .
. .
.
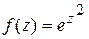 .
.
 , мнимая часть –
, мнимая часть – 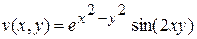 .
. и
и  , т.е. заменить в ней
, т.е. заменить в ней  на
на 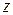 и
и  , то получим
, то получим 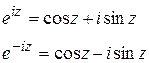
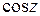 и
и 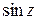 .
.  ,
, 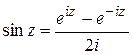 .
.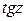 и
и 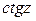 определяются по формулам
определяются по формулам

 . Если учесть, что
. Если учесть, что  , то
, то 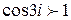 .
.
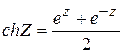

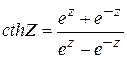

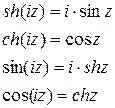
 называется логарифмом числа
называется логарифмом числа  и обозначается
и обозначается 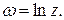
 Тогда
Тогда  .
.
 Следовательно,
Следовательно, 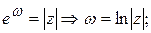
 , где
, где 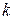 – любое целое число. В результате получим:
– любое целое число. В результате получим: .
.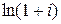 .
.