Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функции
При полном исследовании функции можно придерживаться следующей схемы: 1) указать область определения функции; Если каждому элементу Множество 2) исследовать функцию на четность; Если для любого то функция является четной, если же выполняется равенство то функция является нечетной. В том случае, когда График четной функции симметричен относительно оси
3) найти точки пересечения графика функции с осями координат; Точки пересечения графика функции 4) определить уравнения асимптот графика функции: вертикальные и наклонные; Прямая Прямая или В частности, при Полученная прямая 5) исследовать функцию на монотонность и экстремумы; Найти производную Если при переходе аргумента х через критическую точку а) б) в)
В промежутках где Полученные результаты для наглядности можно оформить в виде таблицы. Эта таблица заполняется следующим образом: 1. В первой строке указываются интервалы, на которые все критические точки разбивают числовую ось и сами точки; 2. Во второй строке указываются знаки первой производной на этих интервалах; 3. В третьей строке описывается поведение функции на каждом интервале (↑ – функция возрастает, ↓– функция убывает). 6) определить интервалы выпуклости и вогнутости, точки перегиба; Найти производную Если на некотором интервале Результаты, так же как и в п. 5 данного алгоритма для наглядности можно оформить в виде таблицы. Эта таблица заполняется следующим образом: 1. В первой строке указываются интервалы, на которые все критические точки второго рода разбивают числовую ось и сами точки. 2. Во второй строке указываются знаки второй производной на этих интервалах. 3. В третьей строке описать поведение функции на каждом интервале (выпукла или вогнута). 7) произвести необходимые дополнительные исследования; Необходимо вычислить значения функции в точках экстремума и в точках перегиба графика функции. Если информации для построения графика недостаточно, найти значения функции в произвольно выбранных вспомогательных точках. По составленным таблицам нетрудно построить график функции. Для этого нужно данные таблиц перенести в декартову систему координат в подходяще выбранном масштабе. 8) построить график функции. Пример 1. Исследовать методами дифференциального исчисления функцию
Решение. 1) Областью определения функции является вся числовая ось, за исключением точек, в которых знаменатель дроби обращается в нуль, то есть
2) Найдем Так как 3) Точка пересечения с осью Точка пересечения с осью т. е. 4) Так как при и Так как данная функция имеет точки разрыва второго рода (точки бесконечного разрыва функции), то существуют вертикальные асимптоты графика функции и их уравнения: Найдем уравнения невертикальных асимптот. Для этого вычислим коэффициенты в уравнении прямой Следовательно, прямая 5) Найдем производную Для того чтобы найти критические точки, решим уравнение: Для нахождения экстремумов и интервалов монотонности функции на числовой прямой отметим все критические точки и определим знак производной в каждом из получившихся интервалов.
Для этого достаточно взять по одной произвольной точке из каждого интервала и вычислить значения производной (рис. 11).
Например: Так как при переходе через критические точки Полученные данные занесем в таблицу: Таблица 4
6) Найдем Определим критические точки. Для этого приравняем вторую производную к нулю: Это уравнение равносильно уравнению Производная второго порядка не существует при На числовой оси отложим все критические точки и определим знаки второй производной аналогично тому, как это сделано в пункте 7 (рис. 12):
При переходе через точку Таблица 5
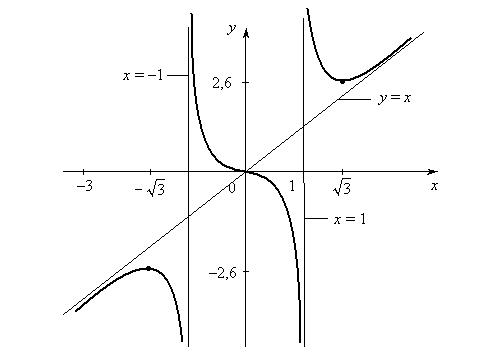
8) Вычислим значения функции в точках экстремума и перегиба: Для более точного построения графика найдем значения функции в дополнительных точках: Теперь построим график функции
Пример 2. Исследовать методами дифференциального исчисления функцию
и построить ее график. Решение. 1) Исходя из того, что известны области определения элементарных функций 2) Так как функция определена только для положительных значений 3) Найдем точки пересечения с осью 4) Данная функция непрерывна на всей области определения. Изучим поведение функции на левом конце области определения, для этого вычислим предел: Отсюда прямая Найдем уравнения невертикальных асимптот. Для этого вычислим (используя правило Лопиталя) следующие пределы: Полученная прямая 5) Найдем Производная равна нулю, когда Производная существует на всей области определения функции
Нанесем область определения и критическую точку на числовую ось и найдем знаки производной Так как при переходе через критическую точку производная меняет знак, то 6) Найдем Производная второго порядка равна нулю, если Нанесем область определения функции и критическую точку на числовую ось (рис. 15). Найдем знаки
При переходе через критическую точку 7) Найдем значения функции при Для более точного построения графика вычислим значения функции По полученным в пунктах 1–7 данным строим график функции
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 74; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.20.193 (0.074 с.) |
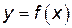 и построении ее графика
и построении ее графика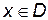 по определенному правилу
по определенному правилу 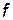 поставлен в соответствие единственный элемент
поставлен в соответствие единственный элемент 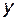 , то говорят, что задана функция
, то говорят, что задана функция  называется независимой переменной или аргументом.
называется независимой переменной или аргументом.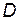 называется областью определения функции. Поэтому, чтобы найти
называется областью определения функции. Поэтому, чтобы найти 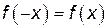 ,
,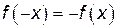 ,
, и
и 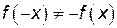 – функция не является ни четной, ни нечетной.
– функция не является ни четной, ни нечетной.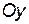 , а график нечетной – относительно начала координат. Таким образом, график четной функции достаточно построить лишь для
, а график нечетной – относительно начала координат. Таким образом, график четной функции достаточно построить лишь для  , а потом, используя симметрию, достроить его на оставшейся части области определения.
, а потом, используя симметрию, достроить его на оставшейся части области определения.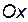 определяются из условия
определяются из условия  , т. е.
, т. е. 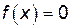 . Точка пересечения с осью
. Точка пересечения с осью 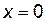 , значит,
, значит, 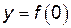 .
. является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , или
, или  .
.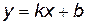 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 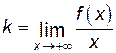 ,
, 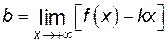
 ,
, 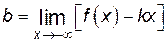 .
.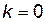 получаем
получаем 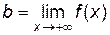 или
или 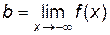 .
.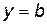 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции  и критические точки, в которых
и критические точки, в которых 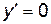 или не существует, и которые лежат внутри области определения функции. Изобразить критические точки на числовой оси и определить знак производной на каждом интервале, слева и справа от каждой критической точки.
или не существует, и которые лежат внутри области определения функции. Изобразить критические точки на числовой оси и определить знак производной на каждом интервале, слева и справа от каждой критической точки.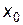 :
: нет экстремума.
нет экстремума. функция возрастает, где
функция возрастает, где 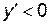 функция убывает.
функция убывает.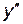 и критические точки, в которых
и критические точки, в которых 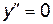 или не существует, а сама функция непрерывна. Изобразить критические точки на числовой оси и определить знак производной на каждом интервале, слева и справа от каждой критической точки. Исследуемая точка х будет абсциссой точки перегиба, если по разные стороны от неё
или не существует, а сама функция непрерывна. Изобразить критические точки на числовой оси и определить знак производной на каждом интервале, слева и справа от каждой критической точки. Исследуемая точка х будет абсциссой точки перегиба, если по разные стороны от неё 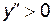 , то функция вогнута (
, то функция вогнута ( 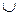 ); если на некотором интервале
); если на некотором интервале 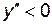 , то функция выпукла (
, то функция выпукла (  ).
).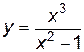 и построить ее график.
и построить ее график.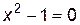 . Отсюда
. Отсюда 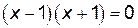 ,
,  ,
,  . Итак, область определения:
. Итак, область определения: 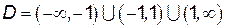 .
. :
: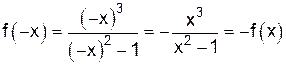 .
.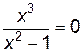 ,
,  ,
,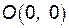 .
.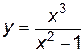 . Причем эти точки являются точками разрыва второго рода, так как
. Причем эти точки являются точками разрыва второго рода, так как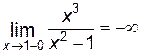 ,
, 
 ,
, 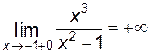 .
.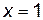 и
и  .
. ,
,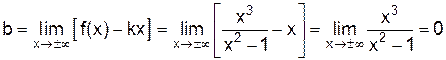 .
. является наклонной асимптотой при
является наклонной асимптотой при 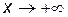 и
и 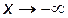 .
.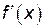 :
: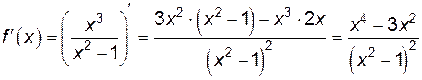 .
.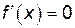 и выясним, в каких точках не существует
и выясним, в каких точках не существует 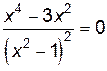 равносильно уравнению
равносильно уравнению 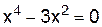 или
или 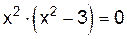 . Отсюда находим стационарные точки:
. Отсюда находим стационарные точки:  ,
, 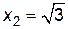 ,
,  . Производная не существует в том случае, когда знаменатель
. Производная не существует в том случае, когда знаменатель  , т. е. при
, т. е. при  ,
, 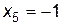 . Таким образом, получили пять критических точек:
. Таким образом, получили пять критических точек: 
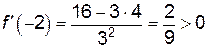 ;
; 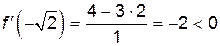 ;
;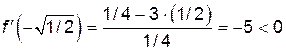 ;
;  ;
; 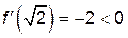 ;
;  .
. производная меняет знак, то эти точки являются точками экстремума функции. В частности, при
производная меняет знак, то эти точки являются точками экстремума функции. В частности, при 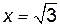 достигается минимум функции, а при
достигается минимум функции, а при 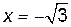 – максимум. Кроме того, на интервалах
– максимум. Кроме того, на интервалах  и
и 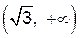 функция возрастает, а на интервалах
функция возрастает, а на интервалах  ,
, 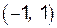 и
и 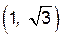 – убывает.
– убывает.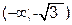
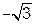
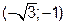
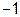
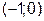
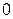
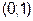
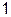
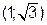

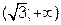
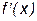
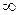
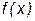
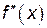 :
:
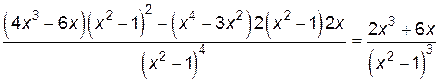
 .
. , откуда
, откуда  . В итоге получили три критические точки:
. В итоге получили три критические точки: 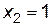 ,
, 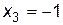 .
. ,
,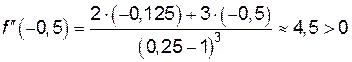 ,
,
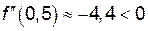 ,
, 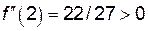 .
.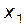 – точка перегиба графика функции. На интервалах
– точка перегиба графика функции. На интервалах 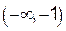 и
и 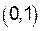 график функции является выпуклым, а на интервалах
график функции является выпуклым, а на интервалах 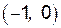 и
и  – вогнутым. Составим таблицу исследования на выпуклость и вогнутость.
– вогнутым. Составим таблицу исследования на выпуклость и вогнутость.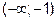
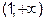
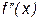
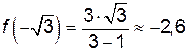 ,
, 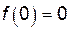 ,
, 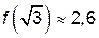 .
.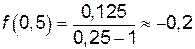 ,
, 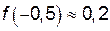 .
.

 и
и 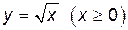 , получаем область определения функции:
, получаем область определения функции: 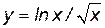 :
:  .
.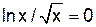 , т. е.
, т. е.  , откуда
, откуда  не существует, так как
не существует, так как  никогда не обращается в нуль. Поэтому график функции пересекается с осями координат в единственной точке –
никогда не обращается в нуль. Поэтому график функции пересекается с осями координат в единственной точке – 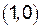 .
.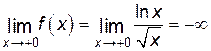 .
.
 ,
,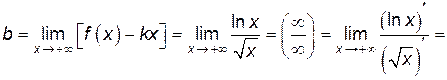
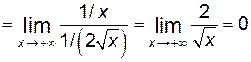 .
.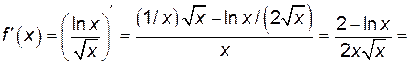
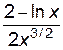 .
. , то есть при
, то есть при 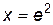 .
.
 на всех интервалах (рис. 14):
на всех интервалах (рис. 14):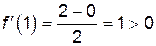 ,
, 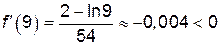 .
.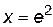 – точка экстремума функции (точка максимума). На интервале
– точка экстремума функции (точка максимума). На интервале 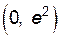 функция возрастает, а на
функция возрастает, а на 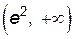 – убывает.
– убывает.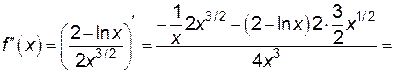
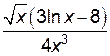 .
.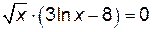 или
или 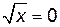 ,
, 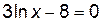 . Отсюда получаем:
. Отсюда получаем:  . Так как
. Так как 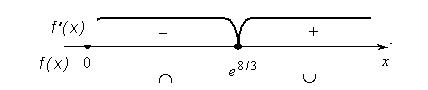
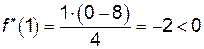 ,
,  .
. 
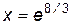 производная второго порядка сменила знак, следовательно, это точка перегиба графика функции. На интервале
производная второго порядка сменила знак, следовательно, это точка перегиба графика функции. На интервале 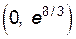 график является выпуклым, а на
график является выпуклым, а на 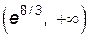 – вогнутым.
– вогнутым.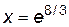 :
: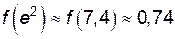 ,
,  .
. в дополнительной точке:
в дополнительной точке:  .
.