Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование кривых на выпуклость, вогнутость
Пусть Кривая, заданная функцией Кривая называется вогнутой на интервале Точка кривой M 0(x 0, f (x 0)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба. Для того, чтобы кривая Для того, чтобы кривая
Исследование кривых на перегиб Е правило - чтобы кривая - чтобы кривая Е правило - чтобы кривая Пример 5. Определитьнаправление выпуклости и точки перегиба кривой Решение - область определения - вся ось абсцисс; область непрерывности - вся ось абсцисс - находим первую производную и вычисляем вторую производную Ищем точки х из области определения функции, в которых Вторая производная равна нулю Исследуем найденные точки, определяя знак
Таблица
Пример 6. Дана кривая у = (х3 – 21 х2)/2. Найти точки перегиба Решение: Находим первую производную у’ =1/2× (3х2 – 42х)
Вычисляем вторую производную У” = 1/2 × (6х -42) =3(х – 7) Вторая производная равна нулю Т.к. вторая производная существует во всей области определения функции, то перегиб может быть лишь при х = 7
Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой. Если
Рассмотрим асимптоты, параллельные оси Oy. Прямая x = x 0 называется вертикальной асимптотой, если хотя бы один из пределов Следовательно, для отыскания вертикальных асимптот нужно найти точки разрыва функции второго рода. Пример 7. Найти вертикальные асимптоты для функции Решение Функция
Прямая Определим числа k и b. Определим коэффициент Если хотя бы один из пределов не существует, то при Аналогично решается вопрос об асимптотах при
Пример 8. Найти асимптоты линии Решение Функция Найдем наклонные асимптоты. Для этого вычислим пределы при так как отсюда значит, b = 0. Итак, прямая y=-x есть наклонная асимптота при
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.195 (0.019 с.) |
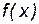 – функция, дифференцируемая на интервале
– функция, дифференцируемая на интервале 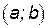 . Рассмотрим кривую, являющуюся графиком функции
. Рассмотрим кривую, являющуюся графиком функции 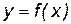 .
.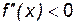
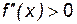
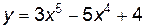
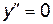 или не существует.
или не существует.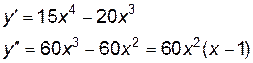
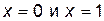 . Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как
. Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как 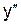 существует всюду.
существует всюду.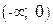
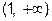
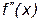
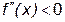
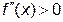

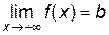 , то прямая
, то прямая 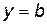 является асимптотой графика
является асимптотой графика 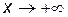 ). Эта асимптота параллельна оси Ox и называется горизонтальной асимптотой Аналогично, прямая
). Эта асимптота параллельна оси Ox и называется горизонтальной асимптотой Аналогично, прямая 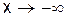 ), если
), если 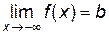 .
.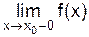 ,
, 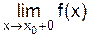 , является бесконечным
, является бесконечным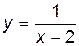 .
.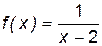 определена и непрерывна во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,
определена и непрерывна во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,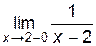 = –¥,
= –¥, 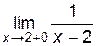 = +¥. Следовательно, прямая х = 2 является вертикальной асимптотой для графика y =
= +¥. Следовательно, прямая х = 2 является вертикальной асимптотой для графика y = 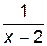 . Кроме того,
. Кроме того, 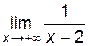 = 0 и
= 0 и 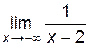 = 0, следовательно, прямая y = 0 является горизонтальной асимптотой при
= 0, следовательно, прямая y = 0 является горизонтальной асимптотой при 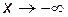 .
.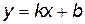 называется наклонной асимптотой функции
называется наклонной асимптотой функции 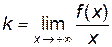
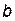 .
.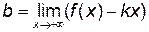
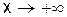 кривая не имеет наклонной асимптоты.
кривая не имеет наклонной асимптоты.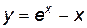 .
.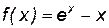 определена, непрерывна на бесконечном интервале
определена, непрерывна на бесконечном интервале 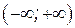 поэтому вертикальных асимптот нет.
поэтому вертикальных асимптот нет.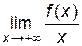 =
= 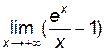 =
= 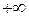 ,
,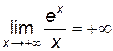 (проверьте это по правилу Лопиталя). Отсюда следует, что при
(проверьте это по правилу Лопиталя). Отсюда следует, что при 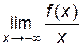 =
= 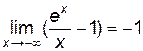 , так как
, так как 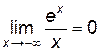 ,
,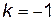 . Далее,
. Далее,