Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Пределы и непрерывностьСтр 1 из 15Следующая ⇒
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ СТАРООСКОЛЬСКИЙ ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ Имени СЕРГО ОРДЖОНИКИДЗЕ» СОФ МГРИ
Г.Н.ЗУБКОВА Н.С.ГАВРЮШКИНА
МАТЕМАТИКА Методическое пособие для студентов 2 курса «общеобразовательный цикл» основной профессиональной образовательной программы
Старый Оскол, 2018 Рецензент СТИ НИТУ МИСиС , доцент, кандидат технических наук О.С. Кравцова
Краткая аннотация: Методическое пособие для являются частью основной профессиональной образовательной программы для студентов 2 курса всех специальностей в соответствии с требованиями ФГОС СПО. Методическое пособие адресовано студентам очной формы обучения. Так как большая часть объема учебной нагрузки студентов отведена на самостоятельную работу, то целью данного пособия является помощь студентам выработать навыки решения практических задач по математике. Оно включает в себя основной теоретический материал и образцы решения типовых задач. Пособие будет полезно тем студентам, которые по различным причинам не смогли посетить все учебные занятия. Также оно будет полезно для подготовки к практическим занятиям, для более успешного понимания и усвоения материала.
Издается по решению ПЦК математики,физики и информатики
Протокол № 9 от __ 06 мая _. 2018 г.
Председатель ПЦК: ____ _______ Г.Н.Зубкова
Количество страниц:_______ Количество условных печатных листов:________
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
В современных условиях специалист среднего звена должен получить более широкую подготовку, чтобы иметь возможность продолжить образование и самообразование, быть востребованным на рынке труда. Это осуществимо при наличии хорошей подготовки специалиста по основополагающим дисциплинам, к которым относится и математика. Данное методическое пособие будет предназначено для студентов II курса всех специальностей. Т.к. большая часть объема учебной нагрузки студентов отведена на самостоятельную работу, то целью данного пособия является помощь студентам выработать навыки решения практических задач по математике. Пособие не заменяет учебник, но помогает как в усвоении теории, так и в приобретении навыков решения задач. Оно включает в себя основной теоретический материал и образцы решения типовых задач. Пособие будет полезно тем студентам, которые по различным причинам не смогли посетить все учебные занятия. Также оно будет полезно для подготовки к практическим занятиям, для более успешного понимания и усвоения материала. ТЕМА 1. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ Теоремы о пределах ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен сумме пределов этих функций, то есть
и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел числителя конечен и отличен от нуля ТЕОРЕМА 4. Предел постоянной величины равен самой постоянной величине:
ТЕОРЕМА 5. Постоянный коэффициент можно выносить за знак предела:
Замечательные пределы Первый замечательный предел равен
Второй замечательный равен
Раскрытие неопределенности 1. Пределы с неопределенностью Правило: для того, чтобы раскрыть неопределенность Пример 1. Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида Пример 2. Вычислить предел
Пример 3. Вычислить предел
2. Пределы с неопределенностью вида Правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенность вида Пример 4. Вычислить предел Решение Сначала попробуем подставить -1 в дробь: Получена неопределенность Разложить числитель на множители. Ответ -7 Пример 5. Вычислить предел 3. Пределы с неопределенностью вида Пример 9. Найти точки разрыва функции, если они существуют, б) найти односторонние пределы в точках разрыва и установить тип точек разрыва функции f(x)=2 x/(3+x) Решение: Функция f(x)=2 x/(3+x) не определена в точке х=-3, значит это точка разрыва. Найдем односторонние пределы в этой точке. Сначала найдем односторонние пределы функции Пример 10. Найти точки разрыва функции и определить их тип f(x)= (x2 – 25)/(x-5) Решение: Область определения функции (- ¥,5)È (5, +¥). Точка х = 5 – точка разрыва Lim (x-5)(x+5)/(x -5)= lim (x+5) при х → 5 Lim (x+5) = 10 при x → 5-0 Lim (x+5) = 10 при x → 5+0 Т.е. односторонние пределы равны и х = 5 – точка устранимого разрыва 1 рода Пример 11. Исследовать функцию на непрерывность и определить вид точек разрыва У= 1/х Решение: Область определения функции (- ¥,0)È (0, +¥). Точка х = 5 – точка разрыва Рассмотрим односторонние пределы Lim 1/x = - ¥ при х → 0-0 Lim 1/x = + ¥ при х → 0+0 Т.е. х=0 – точка разрыва 2 рода Пример 12. Исследовать функцию на непрерывность и определить вид точек разрыва f(x) = x / (1+x2) Решение: Lim x/(1+x2) = - ¥ при х = -1-0 Lim x/(1+x2) = + ¥ при х = -1+0 Т.е. х=-1– точка разрыва 2 рода Пример 13. Исследовать функцию
Решение. Данная функция не определена в точках x = − 1 и x = 1. Следовательно, функция имеет разрывы в точках x = ± 1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках.
Поскольку левосторонний предел при x = − 1 равен бесконечности, то данная точка является точкой разрыва второго рода.
Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода.
Пример 14. Показать, что функция Решение:
также непрерывна при всех x за исключением точки x = 0. Так как то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию
которая будет непрерывной при любом действительном x. Пример 15. Найти точки разрыва функции Решение: Данная функция существует при всех значениях x, однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем "поведение" этой функции вблизи точки x = 0, где ее аналитическое выражение изменяется. Вычислим односторонние пределы при x = 0.
Следовательно, функция имеет точку разрыва первого рода при x = 0. Скачок функции в этой точке равен
При всех других значениях x функция является непрерывной, поскольку обе составляющие функции слева и справа от точки x = 0 представляют собой элементарные функции без точек разрыва. Пример 16. Найти точки разрыва функции Решение: Данная элементарная функция определена для всех x, исключая точку x = 0, где она имеет разрыв. Найдем односторонние пределы в этой точке.
Видно, что в точке x = 0 существует разрыв первого рода Таблица производных На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций. 1. (um)' = m um-1 u' (m принадлежит R1 ) 2. (au)' = au lna× u'. 3. (eu)' = eu u'. 4. (loga u)' = u'/(u ln a). 5. (ln u)' = u'/u. 6. (sin u)' = cos u× u'. 7. (cos u)' = - sin u× u'. 8. (tg u)' = 1/ cos2u× u'. 9. (ctg u)' = - u' / sin2u. 10. (arcsin u)' = u' / 11. (arccos u)' = - u' / 12. (arctg u)' = u'/(1 + u2). 13. (arcctg u)' = - u'/(1 + u2). Пример 1 Найти производную функции y = x 2 − 5 x. Решение. Применяя линейные правила дифференцирования, получаем:
Пример 2 Найти производную функции
Пример 3 Найти производную функции 2√ x − 3sin x. Решение. Используя простейшие правила дифференцирования, получаем:
Пример 4 Найти производную функции y = 3sin x + 2cos x. Решение. Данное выражение представляет собой линейную комбинацию двух тригонометрических функций. Производная имеет следующий вид:
Пример 5 Найти производную функции
Решение Применяя линейные свойства производной, получаем следующий ответ:
Решение Используя приведенные выше формулы дифференцирования, имеем:
Здесь первое слагаемое является степенной функцией с показателем 1/3. Тогда для производной получаем следующее выражение:
Пример 7 Вычислить производную следующей функции
Решение Чтобы решить данный пример с помощью рассмотренных выше правил дифференцирования, перемножим обе скобки и запишем функцию в таком виде:
Теперь легко найти производную:
Пример 8 Найти производную функции Решение Разделив числитель на знаменатель почленно, запишем функцию в виде
Далее, применяя линейные свойства производной, находим:
Производная сложной функции Если функция Пример 9. Найти производную сложной функции y= Решение. Представим функцию y= Пример 10. Найти производную сложной функции y=ln sin x. Решение. Обозначим u=sin x, тогда производная сложной функции y = lnu вычисляется по формуле
y' = (ln u)'u(sin x)'x=
Пример11. Найти производную сложной функции y= Решение. По правилу дифференцирования сложной функции, получим:
Таблица дифференциалов
Производные высших порядков Определение: Пусть F’(x) – производная от функции F(x), тогда производная от функции F’(x) называется второй производной от функции F(x) и обозначается F”(x). Физический смысл: Если функция у = F(x) описывает закон движения материальной точки по прямой, то первая производная F’(x) – мгновенная скорость точки в момент времени, а вторая производная равна скорости изменения функции, т.е. ускорению движущейся точки в этот момент времени. Итак, у"=(у')'. Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")' Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка: y(n)=(y(n-1))'. Производные порядка выше первого называются производными высших порядков. Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уV или у(5)— производная пятого порядка).
Найти вторую производную функции. Первая производная равна
далее находим
Пример 2. Найти вторую и третью производные функции Тогда
Е правило - чтобы кривая
- чтобы кривая Е правило - чтобы кривая Пример 5. Определитьнаправление выпуклости и точки перегиба кривой Решение - область определения - вся ось абсцисс; область непрерывности - вся ось абсцисс - находим первую производную и вычисляем вторую производную Ищем точки х из области определения функции, в которых Вторая производная равна нулю Исследуем найденные точки, определяя знак
Таблица
Пример 6. Дана кривая у = (х3 – 21 х2)/2. Найти точки перегиба Решение: Находим первую производную у’ =1/2× (3х2 – 42х) Вычисляем вторую производную У” = 1/2 × (6х -42) =3(х – 7) Вторая производная равна нулю Т.к. вторая производная существует во всей области определения функции, то перегиб может быть лишь при х = 7
Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой. Если
Рассмотрим асимптоты, параллельные оси Oy. Прямая x = x 0 называется вертикальной асимптотой, если хотя бы один из пределов Следовательно, для отыскания вертикальных асимптот нужно найти точки разрыва функции второго рода. Пример 7. Найти вертикальные асимптоты для функции Решение Функция
Прямая Определим числа k и b. Определим коэффициент Если хотя бы один из пределов не существует, то при Аналогично решается вопрос об асимптотах при Пример 8. Найти асимптоты линии Решение Функция Найдем наклонные асимптоты. Для этого вычислим пределы при так как отсюда значит, b = 0. Итак, прямая y=-x есть наклонная асимптота при Таблица основных неопределённых интегралов
Пример 1. 1. Вычислить неопределенный интеграл
Пример 2. 1. Вычислить неопределенный интеграл
Пример 3. Подведение под знак дифференциала постоянного слагаемого
Пример 4. Подведение под знак дифференциала постоянного множителя
Пример 5.
Замена переменной в неопределённом интеграле Если интеграл Два правила подстановки: 1. Независимую переменную заменяют по формуле x = t(z), где t(z) – дифференцируемая функция. Тогда dx = t'(z) dz, а интеграл
2. Полагаем z = f(x), тогда f(x) dx = g(z) dz. Вычисление интеграла сводится к вычислению
Пример 1.
t = cos(x)
Пример 2. Вычислить интеграл Делаем подстановку t= sin(x), тогда
В результате
Пример 3.
Пример 4.
Формула Ньютона-Лейбница
то Пример 1. применения формулы Ньютона-Лейбница: Пример 2. Вычислить определенный интеграл Решение: Пример 3.
Вычислить интегралы:
Пример 4.
Пример Вычислить определенный интеграл Пример Вычислить определенный интеграл Действия над матрицами Умножение матрицы на число. Любую матрицу можно умножить на любое число, при этом все элементы матрицы умножаются на это число.
Сложение матриц. Две матрицы А и В одинаковой размерности можно сложить, при этом все соответветствующие элементы матриц складываются.
Свойства линейных операций
Умножение матриц Две матрицы можно умножить, если число строк второй матрицы равно числу столбцов первой матрицы. При умножении матриц получается матрица, число строк которой равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы. Элементы матрицы произведения С = АВ находятся по формуле:
где l — число строк второй и число столбцов первой матриц.
Свойства умножения матриц:
Пример. Произведите умножение матриц
Всегда: строки первой матрицы умножаются на столбцы второй матрицы, то есть никогда не будет ситуации когда необходимо будет умножать столбцы первой на строки второй! Важно: матрицы при умножении нельзя менять местами!!! — результат умножения будет другим
Обратная матрица Пусть имеется квадратная матрица n-го порядка
Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка. Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.
Определитель матрицы Для любой квадратной матрицы может быть найдена величина, называемая определителем.
Определитель — это квадратная таблица чисел или математических символов (Δd). Для матрицы второго порядка
Разложение по строке или столбцу Формулы разложения по строке или столбцу:
Первые n формул называются формулами разложения определителя по строке, а вторые n формул называются формулами разложения определителя по столбцу. В этих формулах Минором Mij элемента аij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, получаемой из матрицы А вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент aij/
Правило Саррюса Дописывание двух первых строк или столбцов.
В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33
Пример Вычислить определитель
Решение:
Свойства определителей Свойство 1.
Свойство 2.
Свойство 3.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 75; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.130 (0.304 с.) |
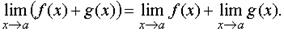 ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть
ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть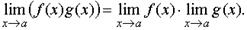 ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть
ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть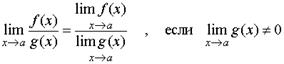
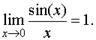
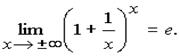
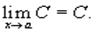
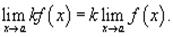

 в старшей степени (т.е.на х2)
в старшей степени (т.е.на х2)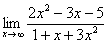
 Здесь неопределенность вида
Здесь неопределенность вида 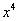
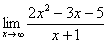 Здесь неопределенность вида
Здесь неопределенность вида 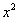 Ответ=2/0=0
Ответ=2/0=0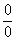
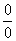 , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
, то для ее раскрытия нужно разложить числитель и знаменатель на множители.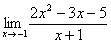
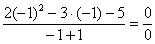
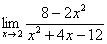
 на непрерывность
на непрерывность

 имеет устранимый разрыв в точке x = 0.
имеет устранимый разрыв в точке x = 0.
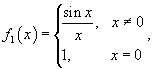
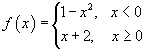 , если они существуют.
, если они существуют.
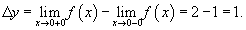
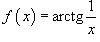 , если они существуют.
, если они существуют.
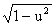 .
.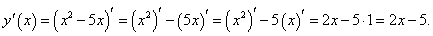
 , где a и b - константы.
, где a и b - константы.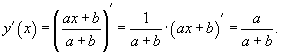

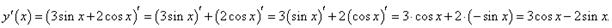

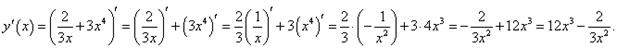
 Пример 6 Найти производную функции
Пример 6 Найти производную функции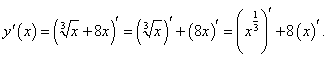

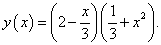


 , не используя формулу производной частного.
, не используя формулу производной частного.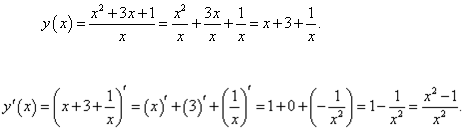
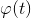 имеет производную в точке
имеет производную в точке  , а функция
, а функция  имеет производную в точке
имеет производную в точке 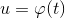 , то сложная функция
, то сложная функция 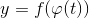 имеет производную в точке
имеет производную в точке  (правило дифференцирования сложной функции).
(правило дифференцирования сложной функции).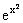 .
.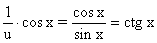
 , u=x4 +1.
, u=x4 +1. y'x =y 'u u'x =(
y'x =y 'u u'x =(  Так как u=x4+1, то y'x=
Так как u=x4+1, то y'x= 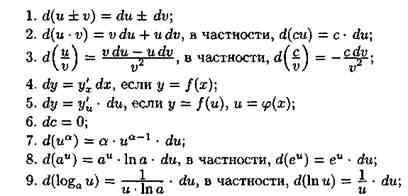
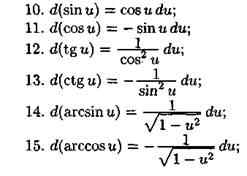

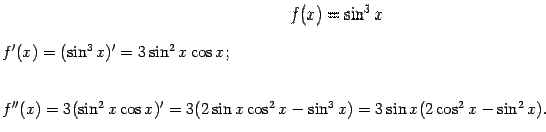 Пример 1:
Пример 1:
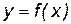 имела перегиб при х = х0 необходимо, чтобы вторая производная в точке х0 либо обращалась в нуль, либо не существовала
имела перегиб при х = х0 необходимо, чтобы вторая производная в точке х0 либо обращалась в нуль, либо не существовала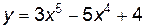
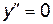 или не существует.
или не существует.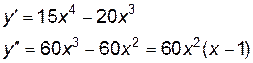
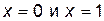 . Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как
. Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как 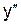 существует всюду.
существует всюду.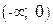
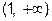
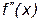
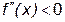
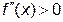

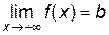 , то прямая
, то прямая 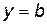 является асимптотой графика
является асимптотой графика 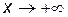 ). Эта асимптота параллельна оси Ox и называется горизонтальной асимптотой Аналогично, прямая
). Эта асимптота параллельна оси Ox и называется горизонтальной асимптотой Аналогично, прямая 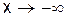 ), если
), если 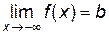 .
.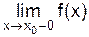 ,
, 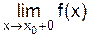 , является бесконечным
, является бесконечным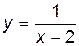 .
.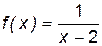 определена и непрерывна во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,
определена и непрерывна во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,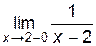 = –¥,
= –¥, 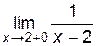 = +¥. Следовательно, прямая х = 2 является вертикальной асимптотой для графика y =
= +¥. Следовательно, прямая х = 2 является вертикальной асимптотой для графика y = 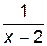 . Кроме того,
. Кроме того, 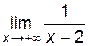 = 0 и
= 0 и 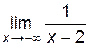 = 0, следовательно, прямая y = 0 является горизонтальной асимптотой при
= 0, следовательно, прямая y = 0 является горизонтальной асимптотой при 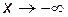 .
.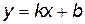 называется наклонной асимптотой функции
называется наклонной асимптотой функции 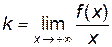
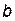 .
.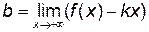
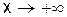 кривая не имеет наклонной асимптоты.
кривая не имеет наклонной асимптоты.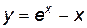 .
.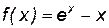 определена, непрерывна на бесконечном интервале
определена, непрерывна на бесконечном интервале 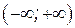 поэтому вертикальных асимптот нет.
поэтому вертикальных асимптот нет.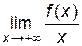 =
= 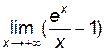 =
= 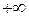 ,
,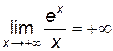 (проверьте это по правилу Лопиталя). Отсюда следует, что при
(проверьте это по правилу Лопиталя). Отсюда следует, что при 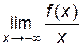 =
= 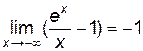 , так как
, так как 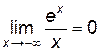 ,
,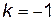 . Далее,
. Далее, 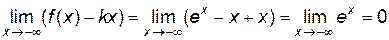


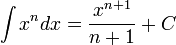
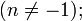
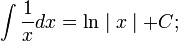
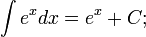
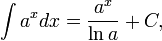
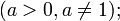
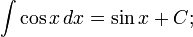
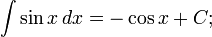
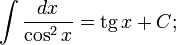
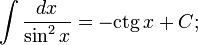


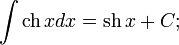
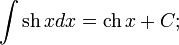

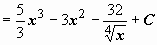
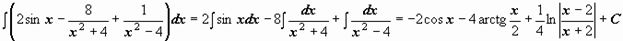

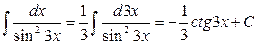
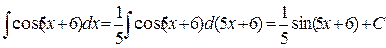
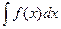 не может быть вычислен непосредственно по основным формулам, то введением новой независимой переменной во многих случаях удается преобразовать подинтегральное выражение f(x) dx. При этом интеграл приводится к табличному или к такому, прием вычисления которого уже известен. Замена переменной и составляет существо метода, называемого методом подстановки.
не может быть вычислен непосредственно по основным формулам, то введением новой независимой переменной во многих случаях удается преобразовать подинтегральное выражение f(x) dx. При этом интеграл приводится к табличному или к такому, прием вычисления которого уже известен. Замена переменной и составляет существо метода, называемого методом подстановки. . После интегрирования получится функция независимой переменной z. Чтобы возвратиться к переменной х, надо определить z через х и подставить это значение вместо z в найденную функцию.
. После интегрирования получится функция независимой переменной z. Чтобы возвратиться к переменной х, надо определить z через х и подставить это значение вместо z в найденную функцию.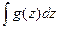 . Чтобы возвратиться к переменной х, надо подставить в полученную функцию f(x) вместо z
. Чтобы возвратиться к переменной х, надо подставить в полученную функцию f(x) вместо z задача сведена к вычислению
задача сведена к вычислению 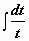 , где
, где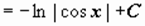

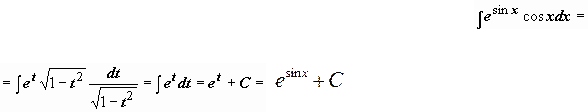
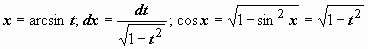

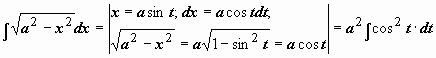

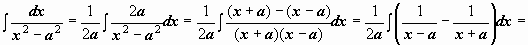
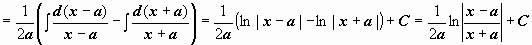
 Если f (x) непрерывна на отрезке [ a, b ], и F (x) - некоторая первообразная функции
Если f (x) непрерывна на отрезке [ a, b ], и F (x) - некоторая первообразная функции 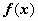 ,
,
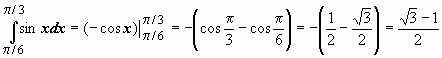 .
.

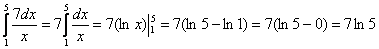
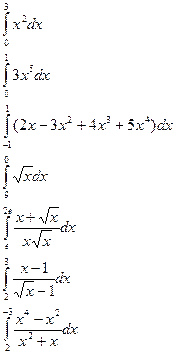
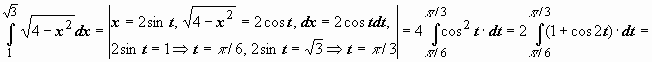
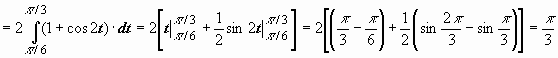
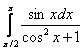
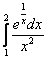
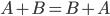
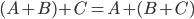
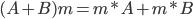
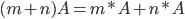
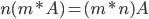
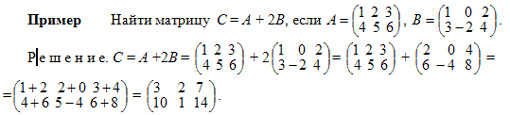
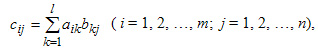
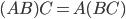
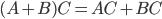
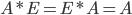 (где Е — единичная матрица)
(где Е — единичная матрица)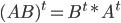
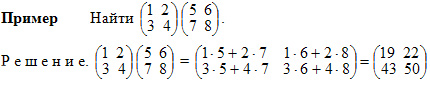

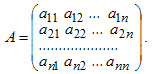
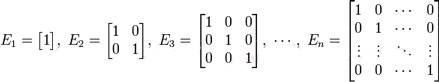
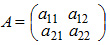 определитель вычисляется по формуле:
определитель вычисляется по формуле: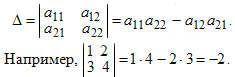
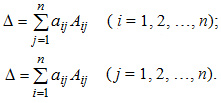
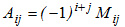 - алгебраические дополнения элементов аij матрицы А, где Mij — миноры элементов аij матрицы А.
- алгебраические дополнения элементов аij матрицы А, где Mij — миноры элементов аij матрицы А.

 двумя способами: с помощью разложения по первой строке и по правилу треугольника.
двумя способами: с помощью разложения по первой строке и по правилу треугольника.