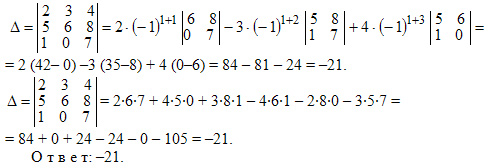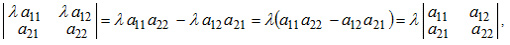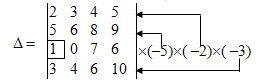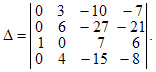Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной. Матрица А = (А1, А2,...Аn) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы
Алгоритм нахождения обратной матрицы Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е. Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е. Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е. Записать обратную матрицу А-1, которая находится в последней таблице под матрицей Е исходной таблицы.
Пример. Для матрицы А найти обратную матрицу А-1
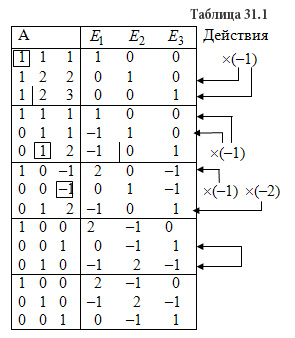
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А-1.
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:
Определитель матрицы Для любой квадратной матрицы может быть найдена величина, называемая определителем.
Определитель — это квадратная таблица чисел или математических символов (Δd). Для матрицы второго порядка
Разложение по строке или столбцу Формулы разложения по строке или столбцу:
Первые n формул называются формулами разложения определителя по строке, а вторые n формул называются формулами разложения определителя по столбцу. В этих формулах Минором Mij элемента аij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, получаемой из матрицы А вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент aij/
Правило Саррюса Дописывание двух первых строк или столбцов.
В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33
Пример Вычислить определитель
Решение:
Свойства определителей Свойство 1.
Свойство 2.
Свойство 3.
Свойство 4.
Свойство 5. Следствие из свойств 32.4 и 32.5: Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторое число, то определитель не изменится.
Свойство 6.
Пример. Вычислить определитель, используя свойства:
Решение: 1. Третью строку умножим на подходящие множители и прибавим к остальным:
получим:
Метод Крамера Решение систем уравнений
Пусть имеется система уравнений:
Обозначим через Δ определитель матрицы системы и через Δj определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы (j=1,2,...n).
Теорема. Если определитель матрицы отличен от нуля, т.е. Δ ≠0, то система имеет единственное решение, которое находится по формуле:
|
|||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 73; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.93.207 (0.012 с.) |
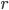 . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
. Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.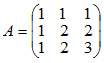
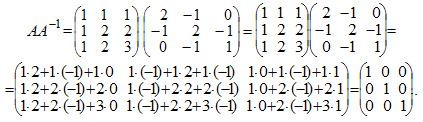
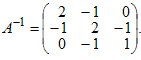
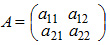 определитель вычисляется по формуле:
определитель вычисляется по формуле: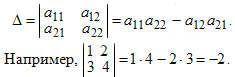
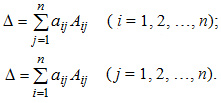
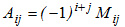 - алгебраические дополнения элементов аij матрицы А, где Mij — миноры элементов аij матрицы А.
- алгебраические дополнения элементов аij матрицы А, где Mij — миноры элементов аij матрицы А.

 двумя способами: с помощью разложения по первой строке и по правилу треугольника.
двумя способами: с помощью разложения по первой строке и по правилу треугольника.