
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл определённого интеграла.
Если
Замечания. 1) Определённый интеграл зависит только от вида функции
2) 3)
Основные свойства определённого интеграла
1. Постоянный множитель можно выносить за знак определённого интеграла, т.е., если
2. Определённый интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых. Так, в случае двух слагаемых
3. Если на отрезке
4. Если
Если
Площадь криволинейной трапеции 5. Теорема о среднем. Если функция
6. Для любых трёх чисел a, b и c справедливо равенство
если только все эти три интеграла существуют. Геометрическая иллюстрация. Если
Тема 14. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Формула Ньютона-Лейбница
Пусть в определённом интеграле
Теорема 1. Если Иными словами, производная от определённого интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела. Замечание. Из теоремы 1 следует, что всякая непрерывная функция имеет первообразную. Действительно, если функция Теорема 2. Если
Эта формула называется формулой Ньютона-Лейбница. Доказательство: Пусть
(так как любые две первообразные от данной функции отличаются на постоянную Пусть x = a, тогда
т.е.
Получаем
При x = b получим формулу Ньютона-Лейбница:
или
Пример:
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.104.214 (0.013 с.) |
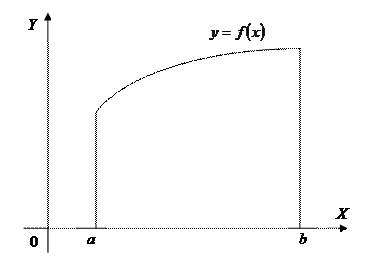
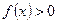 , то интеграл
, то интеграл 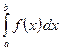 численно равен площади криволинейной трапеции, ограниченной кривой
численно равен площади криволинейной трапеции, ограниченной кривой 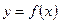 , прямыми
, прямыми 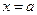 ,
, 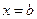 и осью Ox:
и осью Ox: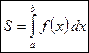 .
.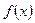 и пределов интегрирования, но не зависит от переменной интегрирования, которую можно обозначить любой буквой:
и пределов интегрирования, но не зависит от переменной интегрирования, которую можно обозначить любой буквой: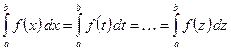 .
.
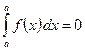
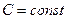 , то
, то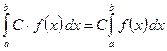 .
. .
.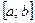 , где
, где 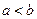 , функции
, функции 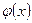 удовлетворяют условию
удовлетворяют условию 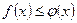 , то
, то .
.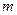 и
и 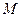 – наименьшее и наибольшее значения функции
– наименьшее и наибольшее значения функции 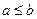 , то
, то .
. , то это свойство иллюстрируется геометрически следующим образом:
, то это свойство иллюстрируется геометрически следующим образом: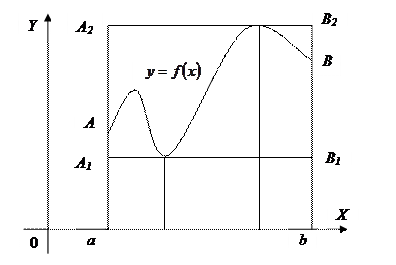
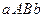 содержится между площадями прямоугольников
содержится между площадями прямоугольников 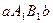 и
и 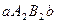 .
.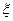 , что справедливо следующее равенство:
, что справедливо следующее равенство: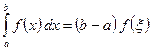 .
.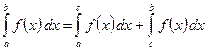 ,
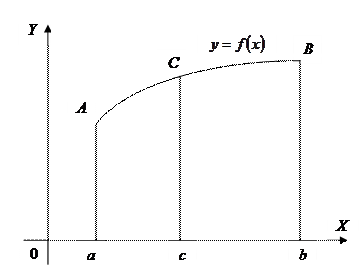
,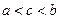 , то площадь трапеции
, то площадь трапеции 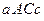 и
и  .
.
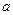 зафиксирован, а верхний предел
зафиксирован, а верхний предел 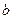 меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть функция верхнего предела. Обозначим эту функцию через
меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть функция верхнего предела. Обозначим эту функцию через 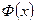 :
: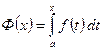 .
. .
. непрерывна на отрезке
непрерывна на отрезке  , то определённый интеграл
, то определённый интеграл  существует, т.е. существует функция
существует, т.е. существует функция  есть какая-либо первообразная от непрерывной функции
есть какая-либо первообразная от непрерывной функции  .
.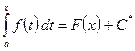
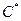 ).
).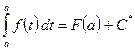 ,
,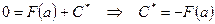 .
.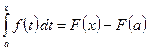 .
.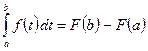
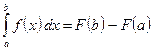 .
.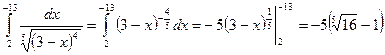 .
.


