
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства неопределённого интеграла.
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е. если
Последнее равенство следует понимать в том смысле, что производная от любой первообразной равна подынтегральной функции. 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению
3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
В частности, 4. Неопределённый интеграл от алгебраической суммы (разности) двух или нескольких функций равен сумме (разности) их интегралов:
5. Постоянный множитель можно выносить за знак интеграла, т.е. если a= const, то
Таблица интегралов
Метод вычисления интегралов, при котором они сводятся к табличным путём применения к ним основных свойств неопределённых интегралов, называется непосредственным интегрированием. Примеры: 1)
2) Используем формулу: При вычислении неопределённого интеграла часто применяется следующее правило: Если Примеры: 1) 2)
Интегрирование методом замены переменной Пусть требуется найти интеграл Сделаем замену переменной в подынтегральном выражении, положив
где
Формула (7) называется формулой замены переменной под знаком неопределённого интеграла. Пример: Делаем замену Замечание. При интегрировании иногда целесообразно подбирать замену переменной в виде не
Пример: Замена:
Интегрирование по частям Формула интегрирования по частям имеет следующий вид:
Этой формулой обычно пользуются, когда подынтегральное выражение Пример:
Замечание. При нахождении
Пример:
Правило интегрирования по частям применяется во многих случаях, например, для интегралов вида
а также для некоторых интегралов, содержащих логарифмическую, обратные тригонометрические функции и корни.
Тема 11. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.3.154 (0.009 с.) |
 , то и
, то и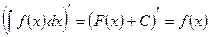 .
. .
.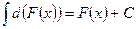 .
. , где
, где 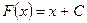 .
.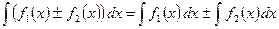 .
.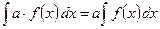 .
.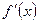



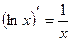

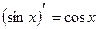
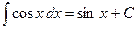
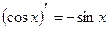
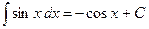
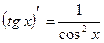

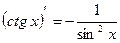

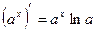

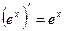
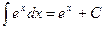
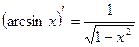

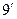 .
.

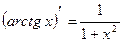
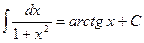
 .
.


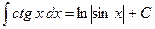

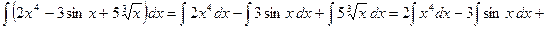
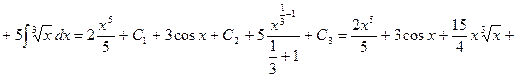
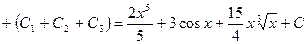
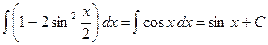
 .
.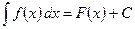 , то
, то 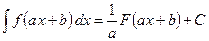 .
.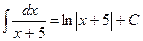
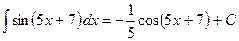
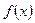 мы не можем, но нам известно, что она существует.
мы не можем, но нам известно, что она существует.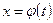 ,
, - непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда
- непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда  и имеет место равенство:
и имеет место равенство: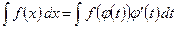 . (7)
. (7)
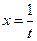 , тогда
, тогда  ,
, 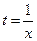 .
.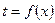 . Пусть, например, требуется вычислить интеграл
. Пусть, например, требуется вычислить интеграл 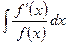 . В результате подстановки
. В результате подстановки  получаем:
получаем: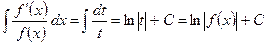 .
.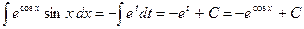
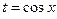 ,
, 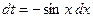 .
.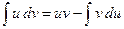 .
.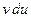 проще, чем подынтегральное выражение
проще, чем подынтегральное выражение  .
.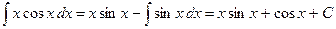
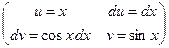
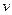 не пишут промежуточную произвольную постоянную
не пишут промежуточную произвольную постоянную 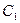 , так как она не оказывает влияния на окончательный результат.
, так как она не оказывает влияния на окончательный результат.
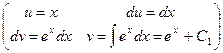
 ,
, 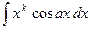 ,
,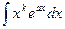 ,
, 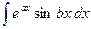 ,
, 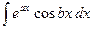 ,
,


