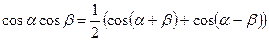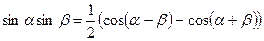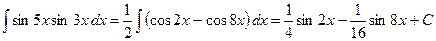Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 12. Интегрирование иррациональных и тригонометрических функций
Интегралы от иррациональных функций
Не от всякой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим те иррациональные функции, интегралы от которых с помощью подстановок приводятся к интегралам от рациональных функций и, следовательно, до конца интегрируются. 1) Пусть k – общий знаменатель дробей
Тогда каждая дробная степень x выразится через целую степень t и, следовательно, подынтегральная функция преобразуется в рациональную функцию от t. Пример:
замена: 2) Этот интеграл сводится к интегралу от рациональной функции с помощью подстановки
где k - общий знаменатель дробей Пример:
подстановка: В ходе решения используем разложение дроби
Интегрирование некоторых классов тригонометрических функций
Рассмотрим интегралы от некоторых классов тригонометрических функций. Покажем, что интеграл вида
с помощью подстановки
Таким образом,
Пример:
подстановка: Рассмотренная подстановка даёт возможность проинтегрировать всякую функцию вида 1) Если интеграл имеет вид 2) подстановка: 3) подстановка: 4) Если подынтегральная функция имеет вид
После подстановки мы получим интеграл от рациональной функции. Примеры: 1)
(используем подстановку 2) Используем подстановку Выделяем целую часть дроби
5) а) m или n – нечётное число, пусть, например,
(подстановка: Таким образом, получен интеграл от рациональной функции. Пример:
подстановка: б)
Пример:
в) Если m и n – чётные и одно из этих значений – отрицательное, используем подстановку Пример:
(подстановка: 6) Интегралы берутся при помощи тригонометрических формул:
Пример:
РАЗДЕЛ 4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Тема 13. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
|
|||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.252.81 (0.015 с.) |
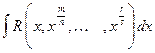 , где R - рациональная функция своих аргументов (запись
, где R - рациональная функция своих аргументов (запись 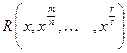 указывает, что над величинами
указывает, что над величинами 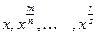 производятся только рациональные операции).
производятся только рациональные операции). . Сделаем подстановку:
. Сделаем подстановку: .
.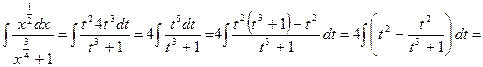
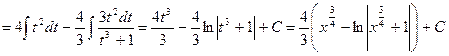

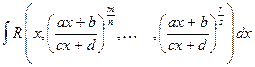
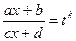 ,
,

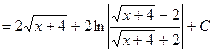

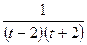 на элементарные дроби:
на элементарные дроби: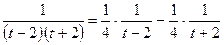
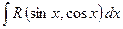 (1)
(1)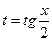 всегда сводится к интегралу от рациональной функции.
всегда сводится к интегралу от рациональной функции.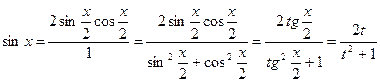 ;
;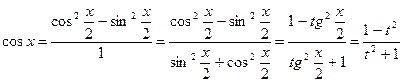 ,
, .
.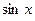 ,
, 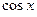 и
и  выразились рационально через t. Подставляя полученные выражения в (1), приходим к интегралу от рациональной функции:
выразились рационально через t. Подставляя полученные выражения в (1), приходим к интегралу от рациональной функции: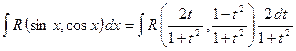 .
.
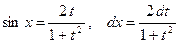
 . Поэтому она называется «универсальной тригонометрической подстановкой». Однако на практике она часто приводит к слишком сложным рациональным функциям, поэтому применяются другие тригонометрические подстановки.
. Поэтому она называется «универсальной тригонометрической подстановкой». Однако на практике она часто приводит к слишком сложным рациональным функциям, поэтому применяются другие тригонометрические подстановки.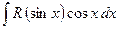 , то используется подстановка
, то используется подстановка 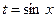 ,
, 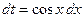 , в результате которой получаем
, в результате которой получаем 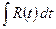 .
.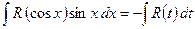
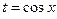 ,
, 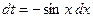

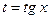 ,
,  ,
, 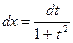
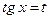 , тогда
, тогда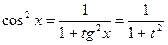 ,
, 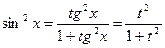 ,
, 
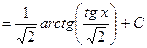

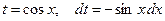 .
. , в результате получаем
, в результате получаем 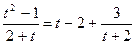 . Тогда
. Тогда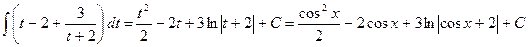
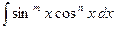
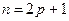 , тогда
, тогда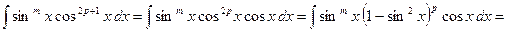

 )
)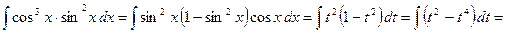

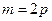 ,
,  , тогда
, тогда
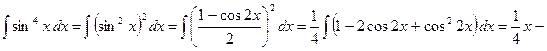

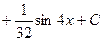
 ), как в случае 4.
), как в случае 4.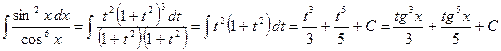
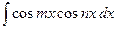 ,
, 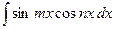 ,
,